关于GC-平坦维数

张文汇,李雪妍

(西北师范大学数学与统计学院,甘肃兰州 730070)



关于GC-平坦维数

张文汇,李雪妍

(西北师范大学数学与统计学院,甘肃兰州 730070)

在任意结合环上引入了模的覆盖GC-平坦维数,对GC-平坦模类的投射可解性给出刻画.证明了模的GC-平坦维数不超过其覆盖GC-平坦维数,并且在GFC闭环上二者相等.

GC-平坦维数;GFC闭环;覆盖GC-平坦维数

0 引言

Gorenstein 同调代数是 Auslader 和 Bridger 等创立并发展起来的,半对偶模的概念首先是由 Foxby 等于1972 年在交换的 Noether 环上引入的[1-3].2007 年,Holm 等在任意结合环上引入了半对偶模的定义[4].目前,相对于半对偶模的 Gorenstein 同调理论的研究已取得了许多重要的研究成果[5-6].

2004 年,Holm 证明了在右凝聚环上 Gorenstein 平坦模类是投射可解类[7].2015 年,Bouchiba 引入了覆盖 Gorenstein 平坦维数的定义[8],它是 Gorenstein 平坦维数的推广.借助这种维数,文献[8]在任意结合环上给出了 Gorenstein 平坦模类是投射可解类的一个等价刻画.2006 年,Hom等引入了GC-平坦模的定义[9].称R-模M是GC-平坦模,如果存在IC(R)⊗R-正合的正合列

使得M≅coker(F1→F0),其中所有的Fi和Fi都是平坦模.2010年,Yang等证明了在Noether环上GC-平坦模类是投射可解类[10].受以上文献启发,我们引入模的覆盖GC-平坦维数,对 GC-平坦模类的投射可解性给出刻画.

文中所提到的环均指有单位元的交换环,除特殊说明,模均指酉模,C总表示半对偶模.N*表示正整数集,I(R)(F(R),GI(R),GF(R))表示内射R-模类(平坦R-模类,Gorenstein内射R-模类,Gorenstein平坦R-模类),FC-fd(M)表示模M的C-平坦维数,M+表示M的示性模HomZ(M,Q/Z).设X是一个R-模类.称序列F=…→F1→F0→F-1→F-2→…是X⊗R-(HomR(X,-))正合的,如果对任意E∈X,复形E⊗RF(HomR(E,F))正合.称X是投射可解类,如果X包含所有的投射R-模,并且在任意正合列0→M1→M2→M3→0中,若M3∈X,则M1∈X当且仅当M2∈X.称X关于扩张封闭,如果在任意正合列0→M1→M2→M3→0中,M1,M3∈X蕴含M2∈X.未说明的概念及记号可参照文献[11-12].

1 预备知识

定义1[1]称R-模C是半对偶模,若满足以下条件:

(1)C有有限生成的投射分解;

(2)R≅HomR(C,C);

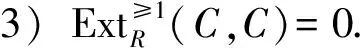
C-内射模类和C-平坦模类定义为

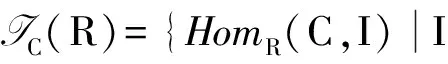
定义2[9]称R-模M是GC-内射模,如果存在HomR(IC(R),-)正合的正合列

使得M≅ker(I0→I1)，其中所有的Ii和Ii都是内射模.

称R-模M是GC-平坦模,如果存在IC(R)⊗R-正合的正合列

使得M≅coker(F1→F0),其中所有的Fi和Fi都是平坦模.

把GC-内射模类和GC-平坦模类分别记作GIC(R)和GFC(R).当C=R时,GIC(R)=GI(R),GFC(R)=GF(R).

模的GC-内射维数和GC-平坦维数的定义为

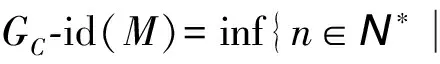
若上述n不存在,则规定Gc-id(M)=+∞;

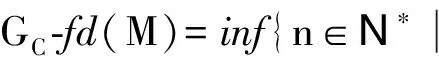
若上述n不存在,则规定GC-fd(M)=+∞.

引理1[13]设M是R模.则以下等价:

(1)M是GC-平坦模;

(3)存在R-模的正合列0→M→F→G→0,其中F是C-平坦模,G是GC-平坦模.

2 覆盖GC-平坦维数

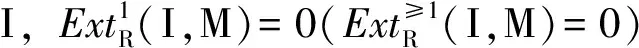
注:(1)当C=R时,余纯C-内射(强余纯C-内射)模即为余纯内射(强余纯内射)模[14],余纯C-平坦(强余纯C-平坦)模即为余纯平坦(强余纯平坦)模.

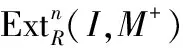
定义4 设M是R-模.如下定义模M的余纯C-内射维数和余纯C-平坦维数:

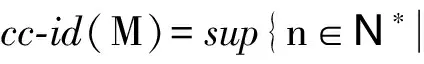
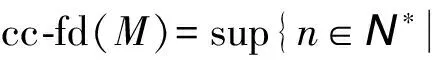
关于余纯 C-平坦维数,我们有如下结论:

命题1 (1)设M是R-模,n是非负整数.则以下等价:

( i )在R-模的正合列0→K→En-1→…→E1→E0→M→0中,若Ei(0≤i≤n-1)是强余纯C-平坦模,则K是强余纯C-平坦模;

( ii )cc-fd(M)≤n;

(iii)在R-模的正合列0→K→Fn-1→…→F1→F0→M→0中,若Fi(0≤i≤n-1)是C-平坦模,则K是强余纯C-平坦模;

(2)设0→N→E→M→0是R-模的正合列.则以下成立:

( i )若E是强余纯C-平坦模,且cc-fd(M)≥1,则cc-fd(M)=1+cc-fd(N).

( ii )cc-fd(M)≤1+max{cc-fd(N),cc-fd(E)}.

(iii)cc-fd(E)≤max{cc-fd(M),cc-fd(N)}.

证明 (1)(i)⟺(ii).设0→K→En-1→…→E1→E0→M→0是R-模的正合列,其中Ei(0≤i≤n-1)是强余纯C-平坦模.令K0≅ker(E0→M),对任意C-内射模I,以函子I⊗R-作用正合列0→K0→E0→M→0,可得长正合列:

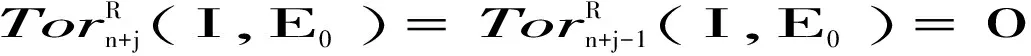
(ii)⟺(iii).设0→K→Fn-1→…→F1→F0→M→0是R-模的正合列,其中Fi(0≤i≤n-1)是C-平坦模.令K0≅ker(F0→M),对任意C-内射模I,以函子I⊗R-作用正合列0→K0→F0→M→0,可得长正合列:

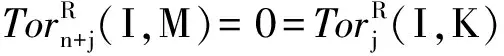
(2)由同调代数方法验证可知. 】

下面引入模的覆盖GC-平坦维数.

定义5 设M是R-模,n是非负整数.如果存在R-模的正合列0→M→E→G→0,其中FC-fd(E)=n,G是GC-平坦模,则定义模M覆盖GC-平坦维数为n,记为CGC-fd(M)=n.

如果满足上述条件的正合列不存在,则规定CGC-fd(M)=+∞.

由引理1易见,CGC-fd(M)=0当且仅当M是GC-平坦模.GC-平坦维数与覆盖GC-平坦维数具有如下关系:

命题2 设R是环,M是R-模.则

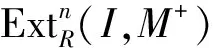
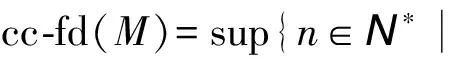
由文献[10]定理3.1知GC-id(M+)≤GC-fd(M).

设CGC-fd(M)=n<+∞,则存在正合列0→M→E→G→0,其中FC-fd(E)=n,G是GC-平坦模.由文献[4]的命题5.3知C-投射模类是预覆盖类,故考虑如下行正合交换图:

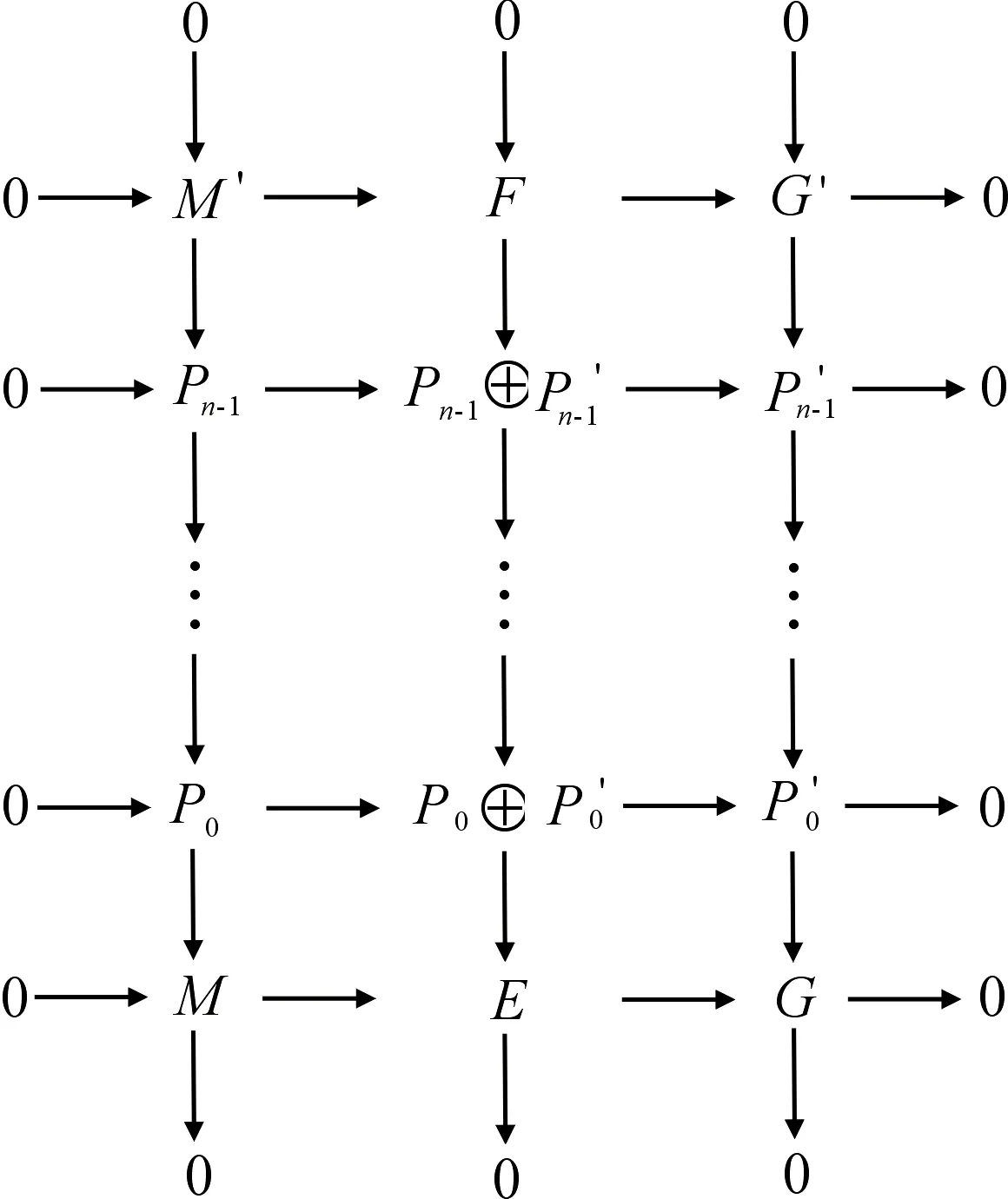
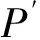
GC-fd(M)≤n=CGC-fd(M).

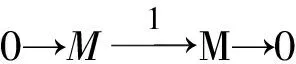
文献[9]中,作者在Noether环上对GC-平坦维数给出等价刻画,在任意结合环上得到如下结论:

定理1 设R是环,M是R-模,n是非负整数.

若CGC-fd(M)=n,则存在R-模的正合列0→K→H→M→0,其中FC-fd(K)=n-1,H是GC-平坦模(若n=0,则K=0).

反之,若存在R-模的正合列0→K→H→M→0,其中FC-fd(K)=n-1,H是GC-平坦模(若n=0,则K=0),则CGC-fd(M)≤n.

证明 设CGC-fd(M)=n.当n=0时,M是GC-平坦模,结论成立.

现设n≥1.由定义知存在正合列0→M→E→G→0,其中FC-fd(E)=n,G是GC-平坦模.由FC-fd(E)=n知存在正合列0→K→E→F→0,其中FC-fd(K)=n-1,F是C-平坦模.考虑拉回图

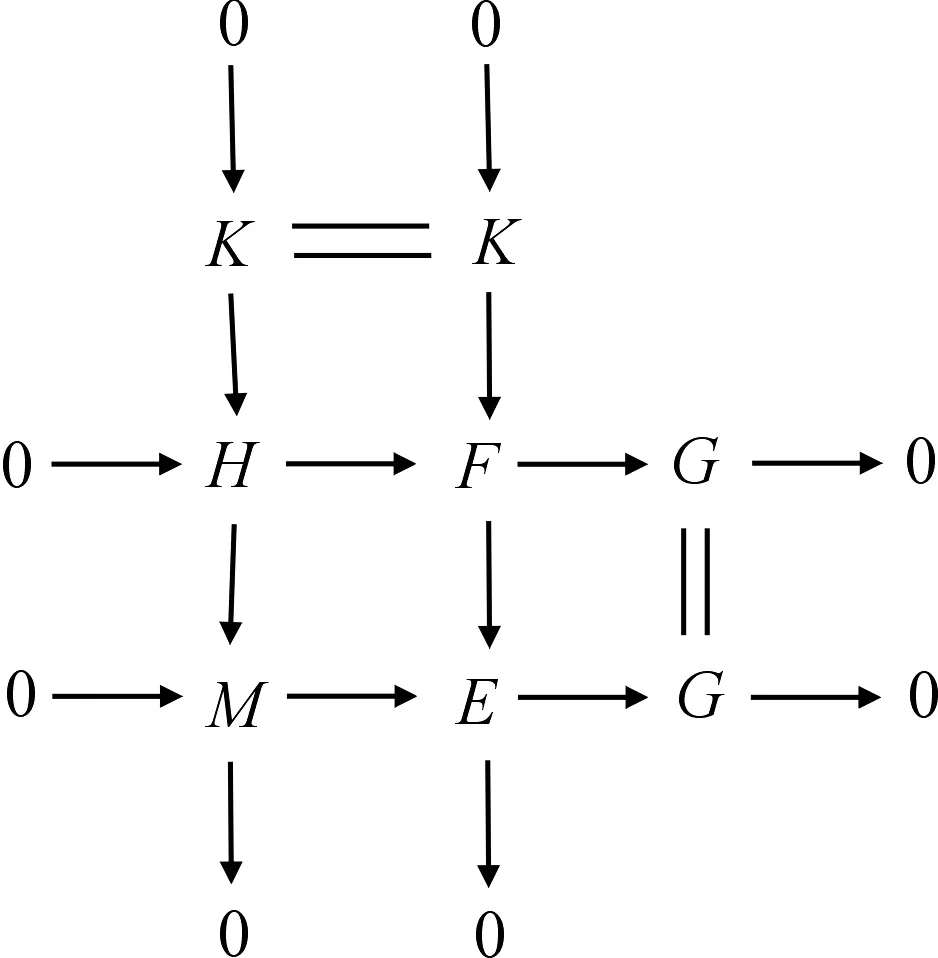
对中间行应用引理1知H是GC-平坦模.正合列0→K→H→M→0即为所求.

反之,考虑推出图

其中F是C-平坦模,G是GC-平坦模.由FC-fd(K)=n-1知FC-fd(E)≤n.由最右列知CGC-fd(M)≤n. 】

命题3 在R-模的正合列0→N→E→M→0中,若M和N是GC-平坦模,则CGC-fd(E)≤1.

证明 由M是GC-平坦模知,存在正合列0→G→F→M→0,其中F是C-平坦模,G是GC-平坦模.考虑拉回图

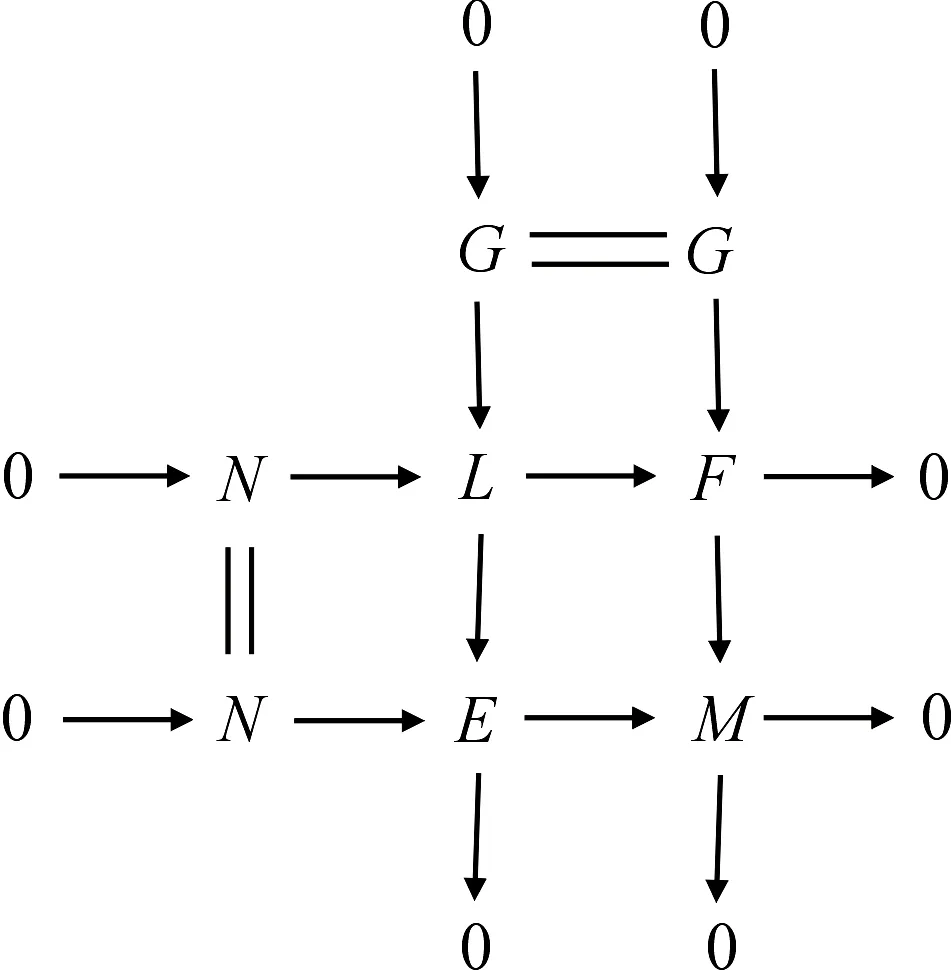
及推出图

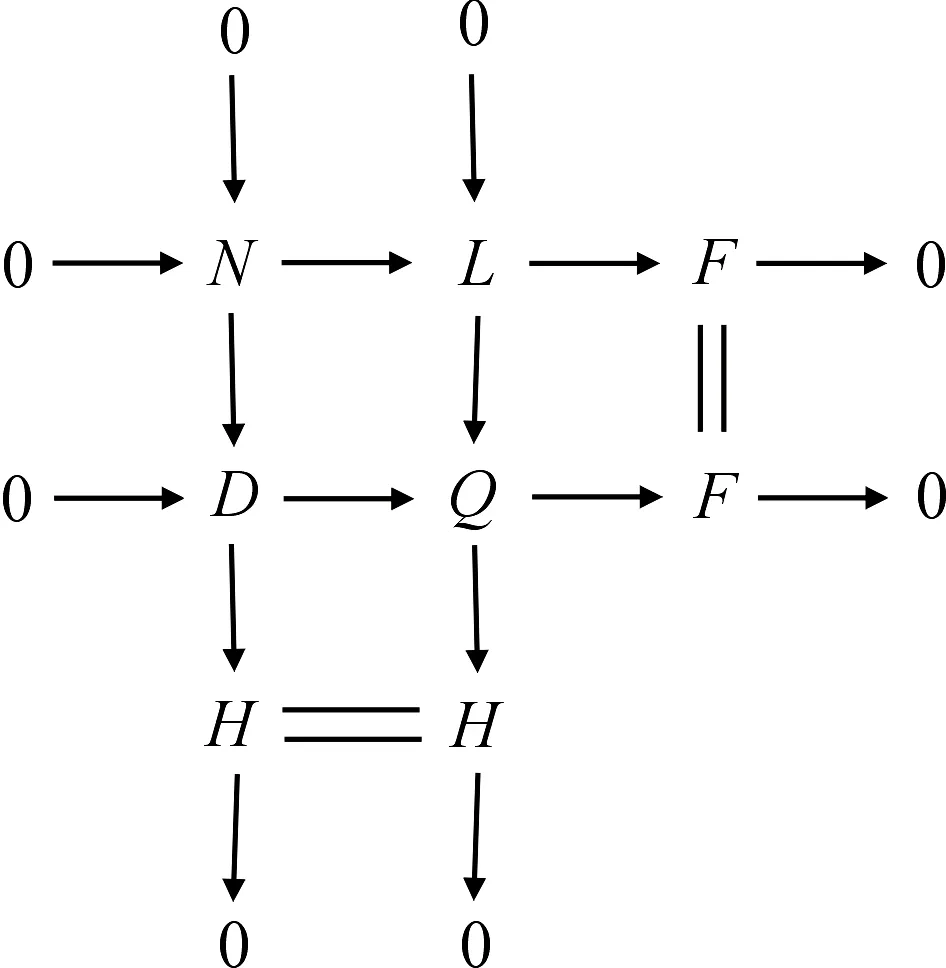
其中D是C-平坦模,H是GC-平坦模.由文献[4]中命题5.2知，C-平坦模关于扩张封闭,故Q是C-平坦模.再对中间列应用引理1知L是GC-平坦模.考虑正合列0→G→L→E→0,因为G和L是GC-平坦模,所以CGC-fd(E)≤1. 】

定义6 设R是环,称R是GFC闭环,如果GFC(R)关于扩张封闭.

由文献[13]知若R是凝聚环,则GFC(R)关于扩张封闭,故凝聚环是GFC闭环.

由文献[15]知,R是GF-闭环当且仅当GF(R)投射可解类.在GFC闭环上,我们有如下结论：

命题4 设R是环,则R是GFC闭环当且仅当GFC(R)是投射可解类.

证明 充分性 显然.

必要性 设0→K→N→M→0是R-模的正合列,其中M和N是GC-平坦模.下证K是GC-平坦模.

由N是GC-平坦模知存在正合列0→N→F→H→0,其中F是C-平坦模,H是GC-平坦模.考虑推出图

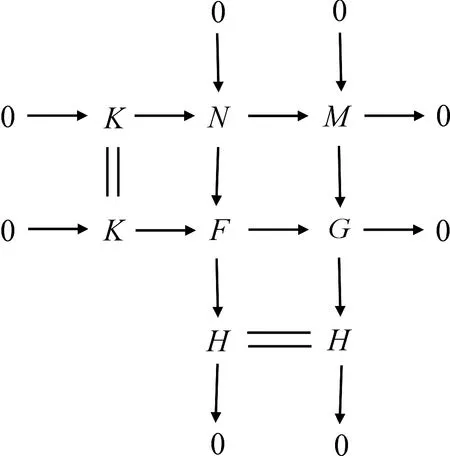
由R是GFC闭环知，G是GC-平坦模.又F是C-平坦模,对中间行应用引理1知K是GC-平坦模. 】

在命题2中,我们证明了对任意R-模M,GC-fd(M)≤CGC-fd(M).在GFC闭环上,有如下结论：

定理2 设R是GFC闭环,M是R-模.则GC-fd(M)=CGC-fd(M).

证明 由命题2知GC-fd(M)≤CGC-fd(M).下证CGC-fd(M)≤GC-fd(M).

设GC-fd(M)=n<+∞,对n进行数学归纳.若n=0,则M是GC-平坦模,结论成立.若n=1则存在正合列0→G1→G0→M→0,其中G1和G0是GC-平坦模.故存在正合列0→G1→G0→M→0,其中F是C-平坦模,H是GC-平坦模.考虑推出图

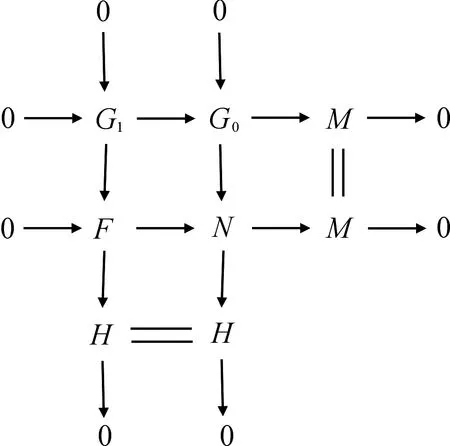
由R是GFC闭环知N是GC-平坦模.又FC-fd(F)=0,对中间行应用定理1知CGC-fd(M)≤1=GC-fd(M).

现设n>1,由GC-fd(M)=n可知存在正合列0→Gn→…→G1→G0→M→0,其中Gi(0≤i≤n)是GC-平坦模.考虑正合列0→N→G0→M→0,其中GC-fd(N)=n-1,G0是GC-平坦模.由归纳假设得,CGC-fd(N)≤GC-fd(N)=n-1,于是存在正合列0→N→D→G→0,其中FC-fd(D)=n-1,G是GC-平坦模.考虑推出图

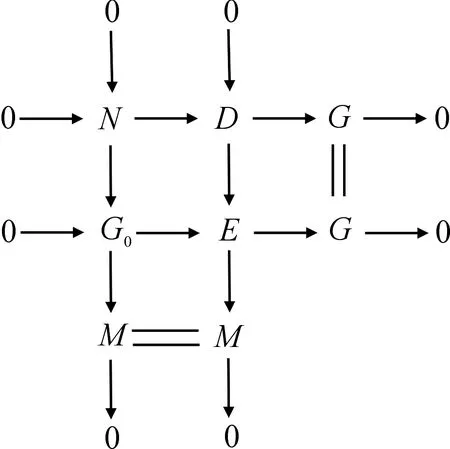
由R是GFC闭环知E是GC-平坦模.又FC-fd(D)=n-1,对中间行应用定理1知，CGC-fd(M)≤n=GC-fd(M). 】

[1]FOXBYHB.Gorensteinandrelatedmodules[J].Math Scand,1972,31:267.

[2] VASCONCELOS W V.DivisorTheoryinModuleCategories[M].Amsterdam:North-Holland Publishing Co.,1974.

[3] GOLOD E S.G-dimension and generalized perfect ideals[J].AlgebraGeometryAppl,CollectionofArticles,TurdyMatSteklov,1984,165:62.

[4] HOLM H,WHITE D.Foxby equivalence over associative ring[J].MathKyotoUniv,2007,47(4):781.

[5] WHITE D.Gorenstein projective dimension with respect to a semidualizing module[J].CommAlgebra,2010,2(1):111.

[6] LIU Z F, HUANG Z Y,XU A M.Gorenstein projective dimension with respect to a semidualizing module[J].CommAlgebra,2013,41(1):1.

[7] HOLM H.Gorenstien homological dimensions[J].JPureAlgebra,2004,189(1-3):167.

[8] BOUCHIBA S.On Gorenstien flat dimension[J].JAlgebraAppl,2015,14(6):1550096.

[9] HOLM H,JO/RGENSEN P.Semi-dualing modules and related Gorenstein homological dimension[J].JPureAppAlgebra,2006,205(2):423.

[10] YANG X Y,LIU Z K.C-Gorenstein projective,injective and flat module[J].CzechoslorakMathJ,2010,60(135):1109.

[11] ENOCHS E,JENDA O.RelativeHomologicalAlgebra[M].New York:de Cruyter,2000.

[12] ROTMAN J J.AnIntroductiontoHomologicalAlgebra[M].New York :Academic Press,1979.

[13] 张亚峰.关于C-Gorenstein范畴的稳定性及同调维数的讨论[D].兰州：西北师范大学,2015.

[14] ENOCHS E,JENDA O.Copure injective resolutions,flat resolvents and dimensions[J].CommentMathUnivCarolinae,1993,34(2):203.

[15] BENNIS D.Rings over which the class of Gorenstein flat modules is closed under extension[J].CommAlgebra,2009,37(3):855.

(责任编辑 陆泉芳)

On GC-flat dimension

ZHANG Wen-hui,LI Xue-yan

(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China )

The coverGC-flat dimension ofR-modules over an associative ring is introduced.It is characterized that the class ofGC-flat modules is projectively resolving.We show that theGC-flat dimension ofR-modules is less than or equal to its coverGC-flat dimension,and they are equivalent over a GFCclosed ring.

GC-flat dimension;GFCclosed ring;coverGC-flat dimension

10.16783/j.cnki.nwnuz.2016.06.001

2016-05-10;修改稿收到日期:2016-07-23

国家自然科学基金资助项目(11201376)

张文汇(1977—)，女，甘肃天水人，副教授，博士，硕士研究生导师.主要研究方向为环的同调理论.

E-mail:zhangwh@nwnu.edu.cn

O 154.2

A

1001-988Ⅹ(2016)06-0001-05