基于分块的压缩重建方法
2016-12-06田小霞
肖 驰,田小霞,2
(1.韩山师范学院计算机和信息工程学院,广东潮州 521041;2.汕头大学工学院,广东汕头 515063)
基于分块的压缩重建方法
肖 驰1,田小霞1,2
(1.韩山师范学院计算机和信息工程学院,广东潮州 521041;2.汕头大学工学院,广东汕头 515063)
图像的压缩重建是当前图像处理中的研究热点,本文提出了一种基于分块压缩的重建方法,该方法首先将图像分成尺寸相同的图像块,在一定的压缩比下各块独自完成SL0重建,最后将各图像块的重建结果拼接成整幅图像.图像块的尺寸与整幅图像的重建时间和质量有密切关系.块尺寸大,重建时间长;块尺寸小,块效应影响图像质量.文中对由尺寸较小图像块组成的重建图像进行维纳滤波,消弱了块效应并提高了图像视觉效果.仿真实验结果显示该方法具有重建时间短和压缩质量高的优势.
SL0压缩;块压缩;维纳滤波;
最近,Donoho[1]和Candès等[2]提出了压缩感知理论(Compression Sensing,CS ).它将采集少量的信号用一个与变换基不相关的观测矩阵投影到一个低维空间,再通过相应重建算法实现了少量投影的精确重建[1-3].它突破了香农采样定理的瓶颈,使得采样数据量小,采样时间短,避免数据存储空间资源浪费.
近年来压缩感知在图像领域上获得了迅猛发展[4-5],但是图像尺寸的大小影响其应用.对尺寸较大的图像进行观测和重建时,其观测矩阵也大,这导致其时间和空间复杂度增大[6].Candes等[7]提出了结构化随机矩阵,但实现过程比较复杂,也不易实现.Lu[8]提出了分块压缩感知算法(Base-block CS,BCS), BCS是把原始图像分为尺寸相同的小图像块,这些图像块采用相同的观测矩阵采样,同时,在信号接收端分别对这些图像块进行重建,组合成整幅图像.由于观测矩阵变小,时间和空间复杂度大大降低.对应用系统来说,瘦身成功,易于传输.故这种技术在图像应用方面具有广阔前景.
本文算法在SL0和BCS的基础上提出,以BCS为框架,压缩重建为优化的SL0算法.
1 压缩感知理论基础
如果信号X是可以压缩的或者在某个变换域上是高维稀疏的,那么可以用一个跟变换基Ψ不相干的测量矩阵φ对信号进行非自适应的、线性的和非相关的投影,得到测量值y,然后根据信号是稀疏的这个先验信息,求解一个带稀疏度约束的欠定方程组[9]
(1)
其中,x=ψα;ψ为稀疏变换基;α为稀疏系数.如果矩阵A=ψα满足URP(UniqueRepresentationProperty),那么(1)式有唯一解.
L0范数的优化是一个NP-Hard[10],上述公式不能直接求解.但它的间接优化算法却很多,主要分为三类:贪婪迭代法,L1凸优化和平滑SL0算法.
MP算法就是不断地从冗余字典中选取与残差最匹配的原子,同时在迭代过程中保证信号的残差最小,再更新信号的拟合值,直到找到所有的原子.信号在选择的原子上的投影不能确保是否正交,故MP算法不能保证一定可以收敛到全局的最优解.Tropp和Gilbert提出了OMP算法[11],OMP算法会在迭代的过程中对所选择的原子做Schmidt正交化,这改善了重建性能.
基追踪算法(BasisPursuit,BP)是用L1范数代替L0范数[12],而L1范数的最优化是一个凸优化问题,因此必然有唯一解.(1)式就可以写为:
(2)
将上述的凸优化问题转化成线性规划问题(Linear Program,LP)加以求解.在重建过程中,该算法需要的测量值个数少,抗噪性能好,有比较高的重建精度.但 BP 算法的高计算复杂度会影响到该算法的大规模应用.梯度投影算法(Gradient Projection for Sparse Reconstruction,GPSR)以梯度下降法作为基础,每次迭代时,沿负梯度方向搜索,同时加入隐变量将原本不可微分的目标函数变成带边界约束的凸二次规划问题[13].GPSR 算法对信号的稀疏度没有要求,但它的计算复杂度也相对较高.
另一种是SL0优化算法, Mohimani 等提出了用平滑范数重建算法(Smoothed Norm,简称 SL0)来最小化范数[14].SL0算法主要利用连续的高斯函数族来拟合不连续的L0范数,然后利用最速下降法来对其最小化,最后对最小化的解进行梯度投影使其符合约束条件.SL0 算法的计算复杂度为O(mn),跟MP算法相当,计算量小.不仅如此,SL0 算法还支持在盲稀疏度的情况下重建原信号.该算法既有贪婪算法的计算复杂度低的优点,又具有凸优化算法的准确性.
2 块压缩
在现有的压缩理论研究中,这些算法通常是将图像的二维信号转换成一维信号来处理,比如将N×N图像的每一列首尾相接组成一个N2×1的列向量,这样一维信号长度很大,导致需要压缩感知的测量矩阵尺寸很大,使得重建过程占用巨大内存,重建速度缓慢.Lu等[8]提出了分块压缩感知算法(Base-block CS,BCS),BCS利用分块的思想解决图像信号占用内存巨大重建效果缓慢的问题.李蕴华[15]和李然等[16]也提出了分块压缩感知模型,前者是对不同块的测量矩阵加权,后者引入排序算子对解码端的随机矩阵重新构建.Abolghasemi等[17]提出测量矩阵尺寸变化的分块法,在运行时间和重建质量获得了很好的效果.BCS提高了存储和传输的效率,在保证重建质量的情况下,缩短了重建时间.
2.1 BCS-SL0算法
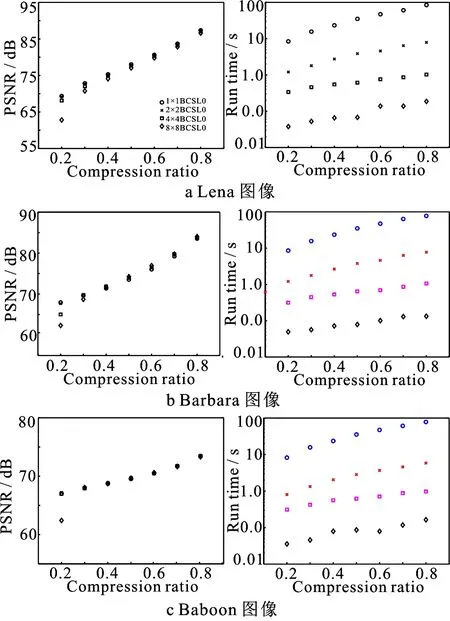
该算法是基于BCS和SL0算法基础上的压缩感知优化算法.它是将图像划分为i个n×n块xi(i=2N/n,对各个子块应用相同的测量矩阵φ,得到观测值向量yi,记为yi=φxi.其中φ为m×n,且m (3) 将所得到各个块的测量值在接收端重建该图像.由于各块采用相同重建算法,只需将得到的重建图像简单组合就得到整个重建图像. 该算法的系统框架如图1所示. 图1 算法的系统框架图 2.2 优化SL0算法 (4) (4)式是一个有约束条件的最优化问题,通过拉格朗日乘子法将其转化成不带约束条件的最优化问题 (5) 从而将离散函数的最优化问题转化成连续函数的最优化问题,通过凸优化的方法对其求解,在迭代过程中采用最速下降法和梯度投影原理,经过多次迭代逐步逼近最优解α′=AT(AAT)-1y. 图2 Lena、Barbara和Baboon在不同压缩比下峰值信噪比和运行时间对比 从图2中可以看到,压缩比低时,峰值信噪比随块尺寸变小而变差.在压缩比高时,四种算法峰值信噪比没有显著差异,这是因为图像分块中有一些块的重建信噪比高从而提高了整幅图像的信噪比.四种算法的运行时间随压缩比增高而迅速增加.但在同一压缩比下,四种算法的重建时间差异较大.从数值上看,(1×1)BCSSL0的重建时间几乎是(2×2)BCSSL0的10倍,是(4×4)BCSSL0的100倍,是(8×8)BCSSL0的1000倍.其中(1×1)BCSSL0表示尺寸为512×512原图整体压缩重建;(2×2)BCSSL0表示将尺寸为512×512原图分为4个256×256图像块的压缩重建;(4×4)BCSSL0表示将尺寸为512×512原图分为16个128×128图像块的压缩重建;(8×8)BCSSL0表示将尺寸为512×512原图分为64个64×64图像块的压缩重建.本算法时间复杂度的优势得到充分的体现.图3给出了在0.5压缩比下不同尺寸块的重建效果. 图3 在0.5压缩比下不同尺寸块的重建效果 从这些图像对比中可以看出,视觉的差异不是很显著,(1×1)BCSSL0重建图像的峰值信噪比与(8×8)BCSSL0重建图像的峰值信噪比多1 dB左右. 由于图像分块压缩重建,重建图像中会有块效应.如Baboon图像中眼睛下方的区域.图像分块重建产生块效应主要有三个原因:块稀疏度不均匀、频谱泄露和块尺寸受限[16].为了减小块效应,本文对重建的图像进行维纳滤波,得到的图像视觉效果较好,但峰值信噪比略有降低.图4为维纳滤波后的重建图像. 图4 在0.5压缩比和(8×8)BCSSL0下重建图像的维纳滤波效果 三个各有特点的图像在分为不同尺寸的块和不同压缩比下,经过维纳滤波的重建图像和未经过维纳滤波重建图像的峰值信噪比对比见图5所示. 图5 在(8×8)BCSSL0下不同压缩比的重建图像和经过维纳滤波重建图像的信噪比对比 本文提出的BCS-SL0方法集聚了BCS和SL0的优点,不仅不需要预先设置信号的稀疏度,而且速度提高一个数量级.重建图像的质量虽略有下降,但对压缩感知实时系统来说,这点可以接受;另一个问题是重建图像的块效应,采用维纳滤波对重建图像过滤,虽视觉效果提升,但峰值信噪比略有下降了.在保证重建时间的情况下,提高重建质量和视觉效果是下一步的研究目标. [1] DONOHO D L.Compressed sensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289. [3] 闫敬文,刘蕾,屈小波.压缩感知及应用[M].北京:国防工业出版社,2015. [4] 詹旭,马将,付克兰.基于压缩传感的灰度图像水印算法[J].西北师范大学学报(自然科学版),2016,52(1):47. [5] 李锦珑,张维昭,马宏锋,等.基于 HA LCON 的车牌识别技术研究[J].西北师范大学学报(自然科学版),2015,51(6):54. [6] CANDES E,ROMBERG J.Sparsity and incoherence in compressive sampling[J].InverseProblems,2007,23(3):969. [7] CANDES E J,ROMBERG J,TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEETransactionsonInformationTheory,2006,52(2):489. [8] LU G.Block compressed sensing of natural images[C]//InternationalConferenceonDigitalSignalProcessing.Cardiff UK:IEEE,2007:403. [9] FOWLER J E,MUN S,TRAMEL E W.Block-based compressed sensing of images and video[J].FoundationsandTrendsinSignalProcessing,2012,4(4):297. [10] CANDES E J,TAO T.Decoding by linear programming[J].InformationTheory,IEEETransactions,2005,51(12):4203. [11] TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655. [12] CHEN S S,DONOHO D L,SAUNDERS M A.Atomic decomposition by basis pursuit[J].SIAMJournalonScientificComputing,1998,20(1):33. [13] FIGUEIREDO M A T,NOWAK R D,WRIGHT S J.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J].SelectedTopicsinSignalProcessing,IEEE Journal of,2007,1(4):586. [14] MOHIMANI H,BABAIE-ZADEH M,JUTTEN C.A fast approach for overcomplete sparse decomposition based on smoothed norm[J].SignalProcessing,IEEETransactionsonInformationTheory,2009,57(1):289. [15] 李蕴华.一种改进的图像分块压缩感知模型[J].计算机工程与应用,2011,47(25):186. [16] 李然,干宗良,朱秀昌.基于分块压缩感知的图像全局重建模型[J].信号处理,2012,28(10):1416. [17] ABOLGHASEMI V,FERDOWSI S,SANEI S.A block-wise random sampling approach:compressed sensing problem[J].JournalofAIandDataMining,2015,3(1):93. (责任编辑 孙对兄) Compression reconstruction methods based on block XIAO Chi1,TIAN Xiao-xia2 (1.College of Computer and Information Engineering,Hanshan Normal University,Chaozhou 521041,Guangdong,China;2.College of Engineering,Shantou University,Shantou 515063,Guangdong,China) Image compression and reconstruction are a hot Copic in image processing.This paper presents a new reconstruction method based on block.The new method firstly divides the image into the same blocks according to a certain rule.Then it applies the SL0 algorithm to every block,which is reconstructed successively.Finally,we scrape up the whole from blocks.The size of the block can affect the time and quality of the reconstruction image.If the size of the block is too small that blocking artifacts do harm to the quality of the reconstruction image.In this paper,the Wiener filtering is employed to improve the quality of the reconstruction image which has many small blocks.The simulation results show that the method has the advantages of the reconstruction time and the compression quality. SL0 compression method;block compressed sensing;Wiener filtering 10.16783/j.cnki.nwnuz.2016.06.011 2015-12-24;修改稿收到日期:2016-07-06 韩山师范学院学科建设专项基金(2013LYM0055);潮州市科技引导计划项目(2012S13) 肖驰(1971—),男,湖南邵阳人,讲师.主要研究方向为图像处理及软件测试. E-mail:553293364@qq.com TP 391.4 A 1001-988Ⅹ(2016)06-0051-05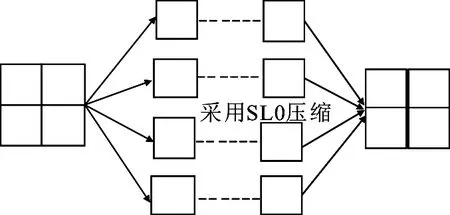

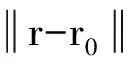
3 仿真结果分析




4 结束语
