粘结压电材料的梯度压电压磁层合中的界面裂纹分析

周春梅

(宁夏师范学院数学与计算机科学学院,宁夏固原 756000)



粘结压电材料的梯度压电压磁层合中的界面裂纹分析

周春梅

(宁夏师范学院数学与计算机科学学院,宁夏固原 756000)

分析了粘结压电材料的梯度压电压磁层合中的界面裂纹，在非渗透性边界条件情况下，假定材料物性参数呈指数变化，运用Fourier变换将问题转化为奇异积分方程.然后利用Guass-Chebyshev积分公式对奇异积分方程进行数值求解，得到了裂纹尖端的应力、电位移和磁通量强度因子.最后考察了裂纹长度和梯度参数等因素对强度因子的影响.

功能梯度压电压磁材料;界面裂纹;奇异积分方程;应力强度因子

压电压磁材料作为一种新型智能材料，近些年来，成为国内外众多学者研究的热点.由于它有响应快、精度高、频域宽等特点，压电压磁材料被广泛应用于航天和医疗等方面.靳静等[1]采用积分变换和奇异积分方程技术研究了压电压磁双层材料界面裂纹断裂的特性.马鹏等[2]在假设压磁材料没有电势，且在界面上压电材料的电势和压磁材料的磁势均为零的情况下，研究了压电压磁界面裂纹二维断裂问题.赵兴等[3]研究了界面性能由“弹簧”模型表征，材料性能沿厚度方向呈指数变化的非理想界面功能梯度压电/压磁层状半空间结构中的SH波.时朋朋等[4]分析了功能梯度压电压磁球对称问题的静力响应，给出了不同梯度参数下结构内部径向应力、环向应力、电势和磁势的分布.孟广伟等[5]提出了含孔功能梯度压电材料板的力电耦合无网络伽辽金法，结果表明此方法不但精度高，还可求解任意梯度函数的功能梯度压电材料问题.

1 问题及边界条件

粘结压电材料的梯度压电压磁层中含有半长为a的裂纹问题如图1所示.x-y平面为横观各向同性.裂纹表面上受到反平面的力载荷τxy=τ(x)、平面内的电位移Dy=D(x)及平面磁通量By=B(x).

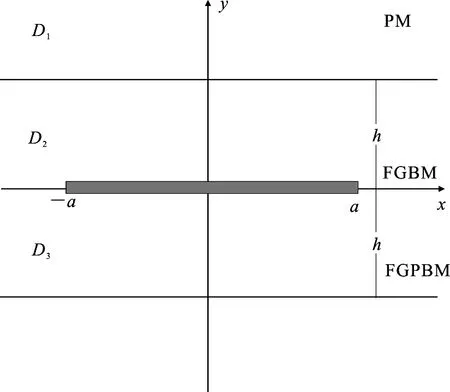
图1 粘结压电材料的梯度压电压磁层合中的界面裂纹几何模型

对于反平面问题，应力分量只剩下两个分量τxz和τyz；位移矢量只有一个w分量，其余的应力分量都等于零.

压电压磁复合材料的本构方程为

(1)

(2)

(3)

其中,τyz(k),By(k)和Dy(k)分别为反平面剪应力、平面磁通量和平面电位移；ψk,wk和φk为反平面磁势，位移和电势；下标k=1,2,3分别对应区域D1,D2和D3.

反平面动力学问题的控制方程为

(4)

设材料性质沿y轴方向按指数函数梯度分布

(5)

其中,c0,e0,ε0,q0,d0,μ0,ρ0和β分别为剪切模量、压电系数、介电常数、压磁系数、磁电系数、导电率、密度和功能梯度参数.

将(1-3)式代入(4)式并利用(5)式，得到材料的控制方程为

(6)

(7)

(8)

由此可得

(9)

该问题的边界条件为[6]

(10)

(11)

(12)

2 求解

采用Fourier积分变换及其逆变换求解上面的控制方程得到位移、电势和磁势的表达式分别为

(14)

(15)

(16)

其中,Aij(s),Bij(s),Cij(s)(i,j=1,2),E(s)和F(s)都为未知函数.

引入三个位错函数g1(x),g2(x)和g3(x)[7]

(17)

(18)

(19)

将(13)～(15)式代入(17)～(19)式中，并利用条件(11)可得

(20)

当x∈[-a,a]时，可得

(21)

(22)

(23)

应用Fourier积分变换和边界条件(10)～(12)得到系数Aij(s),Bij(s)和Cij(s),(i=1,2,3;j=1,2,3).进而由本构方程和边界条件得到应力、电位移和磁通量的形式解为[8]

(24)

(23)式为奇异积分方程，可由Gauss-Chebyshev积分公式数值求解[9].

3 强度因子的数值计算

利用Chebyshev多项式动应力强度因子、电位移强度因子和磁通量强度因子为[4]

(25)

(26)

(27)

(28)

(29)

(30)

4 数值结果

假定在图1中压电材料和压电/压磁材料分别为PZT-4和BaTiO-CoFe2O4.数值结果由图2和图3给出.

由图2可知，在不同β下，强度因子K3随高度h变化，当固定β值时，裂纹尖端处的强度因子随着材料带宽h的增大而减小，从某一时刻开始，几乎趋于一个定值；当固定h值时，裂纹尖端处的强度因子随着材料梯度参数β的增大而减小.

从图3可以看出，在不同h下，强度因子K3随裂纹半长a的变化，当固定h值时，裂纹尖端处的强度因子随着裂纹半长a的增大而增大；当固定a值时，裂纹尖端处的强度因子随着材料带宽h的增大而减小.

图2 不同β下，强度因子K3随高度h的变化

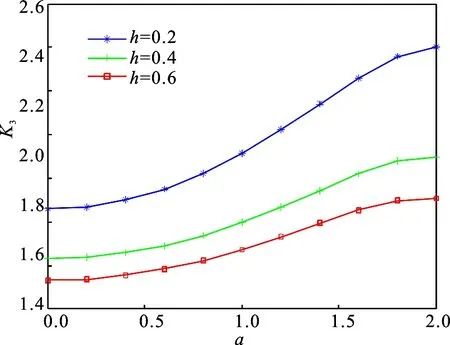
图3 不同h下，强度因子K3随裂纹半长a的变化

5 结论

分析了粘结压电材料的梯度压电压磁层合中的界面裂纹.在非渗透性边界条件下，利用Guass-Chebyshev积分公式和奇异积分方程对问题进行了求解，最后给出了裂纹尖端强度因子受材料特性及裂纹长度的影响规律，即裂纹尖端强度因子随着裂纹半长的增大而增大，随着材料梯度参数的增大而减小，随着材料带宽的增大而减小.

[1] 靳静,马鹏.压电压磁双层材料界面裂纹断裂特性进一步分析[J].工程力学,2013,30(6):327.

[2] 马鹏,冯文杰,靳静.压电压磁双层材料界面二维裂纹分析[J].工程力学,2011,28:163.

[3] 赵兴,田若萌,赵存宝,等.非理想界面功能梯度压电/压磁层状半空间结构中的SH波[J].工程力学,2014,31(5):251.

[4] 时朋朋,李星.功能梯度压电压磁球对称问题的静力响应[J].工程力学，2014,31(5):56.

[5] 孟广伟,王晖,周立明,等.含孔功能梯度压电材料板的力电耦合无网络伽辽金法[J].中南大学学报，2015,46(11):4015.

[6] DEEG W F.TheAnalysisofDislocation,CrackandInclusionProbleminPiezoelectricSolids[D].California:Stanford University,1980.

[7] ERDOGAN F,GUPTA G D.On the numerical solution of singular integral equations[J].QuarterlyofAppliedMathematics.1972,1:525.

[8] LI C Y,WENG G J.Anti-plane crack problem in functionally graded piezoelectric materials[J].ASMEJournalofAppliedMechanics,2002,69:481.

[9] Muskhelishvili.奇异积分方程[M].上海：上海科学技术出版社，1966.

(责任编辑 孙对兄)

Analysis of the interfacial crack of functionally graded piezoelectric/piezomagnetic layers bonded to the piezoelectric materials

ZHOU Chun-mei

(School of Mathematics and Computer Science,Ningxia Teachers Univercity,Guyuan 756000,Ningxi,China)

In this paper,the interfacial crack of functionally graded piezoelectric and piezomagnetic layers bonded to the piezoelectric materials is analyzed.In the impermeable boundary conditions,based on the assumption of the material property parameters to the exponential,the question is turned into the singular integral equations using Fourier transform.Then,the numerical results of the singular integral equations are obtained through the Guass-Chebyshev integral formula.As a result,the stress intensity factors,electric displacement factors and piezomagnetic intensity factors at crack tips are obtained.In the end,the effects of material graded parameter and the length of the crack on the intensity factors are explored.

functionally graded piezoelectric/piezomagnetic materials;interfacial crack;singular integral equation;stress intensity factor

10.16783/j.cnki.nwnuz.2016.06.008

2016-01-10;修改稿收到日期:2016-03-20

宁夏高等学校科学技术研究资助项目(njg201422218,ZD20142221)；宁夏自然科学基金资助项目(NZ16257，NZ16253，NZ16255)

周春梅(1982—),女，宁夏固原人,讲师，硕士.主要研究方向为复分析及其在力学中的应用.

E-mail:453315811@qq.com

O 343.7

A

1001-988Ⅹ(2016)06-0038-04