Problem of Circular Hole in Thermopiezoelectric Media with Semi－permeable Thermal Boundary Condition

Song Haopeng（宋豪鹏），Hu Wei（胡巍），Gao Cunfa（高存法）

State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics ＆Astronautics，Nanjing，210016，P.R.China

1 Introduction

Widespread attention has been given to the thermal stress problems with inclusions，holes or cracks.For example，Florence and Goodier［1］，Sih［2］，Parton［3］，Zhang and Hasebe［4］，Chao and Shen［5－6］，Kattis and Patia［7］，and Kaminskii and Flegantov［8］studied the thermal stress problems in isotropic media，and also Sturla and Barber［9］，Hwu［10－11］，Tarn and Wang［12］，Chao and Chang［13］，Lin et al［14］and Shen and Kuang［15］discussed the thermal stress problems in anisotropic materials.

In recent years，the thermo－electric－mechanical coupling problem in thermopiezoelectric media with holes or cracks has also received much attention with increasingly wide application of thermopiezoelectric materials in the engineering.Gao and Wang［16］studied the 2Dproblem of thermopiezoelectric materials with cracks by means of the Parton assumption，i.e.the crack is considered as a thin slit and thus the normal components of electric displacement and the tangential component of electric field are assumed to be continuous across the slit［3］.They also presented an exact solution for the problem of an elliptic hole or a crack in a thermopiezoelectric solid［17］.The frac－ture analysis of a cracked thermopiezoelectric medium with thermoelectric loading has been dealt with by Ueda［18］.

However，all the references above supposed that the normal component of the heat flow could be treated as zero at the rim of the hole.In the present work，a semi－permeable thermal boundary condition is proposed to discuss the influence of the thermal conductivity acting on the stress and heat flow around the hole.

2 Basic Equations

The governing equations for piezothermoelastic problem can be expressed，in the stationary case without body force，extrinsic bulk charge and heat source，as folllows：

Governing equation

Constitutive equation

where qi，λij，T（i，j＝1，2）are the heat flux，heat conduction coefficients and temperature，respectively.

From Eqs.（1－2），we have

whereμt＝（－λ12＋iκt）／λ22，κt＝（λ11λ22－）1／2，λ11λ22－λ212＞0.

Substituting Eq.（3）into Eq.（2）yields

and

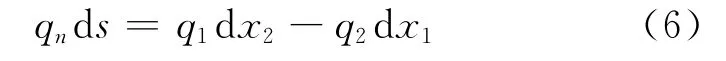
On the other hand，the resultant heat flow Qcan be expressed as

Substituting Eqs.（4－6）into Eq.（7）yields

The semi－permeable boundary conditions of heat flow is

whereλ1andλ2are two thermal conduction coefficients.

The complete set of governing equations are

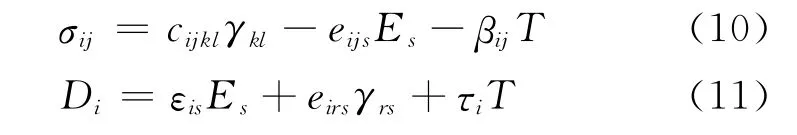
where cijkl＝cjikl＝cijlk＝cklij；ekij＝ekji，εij＝εji；βij＝βji；i，j，k，l＝1，2，3，….σ，D，Eare stress，electric displacement and electric field，respectively；cijkl，ekij，εij，βijandτithe elasticity constants，piezoelectricity constants，dielectric constants，stress－temperature coefficients and pyroelectric coefficients，respectively.

Equilibrium equation are

Substituting Eqs.（10－11）into Eq.（12）yields

Introduce two function vectors u＝（u1，u2，u3，φ）Tandφ＝（φ1，φ2，φ3，φ4）T。

The homogeneous solutions of Eq.（13）are

and the particular solutions are

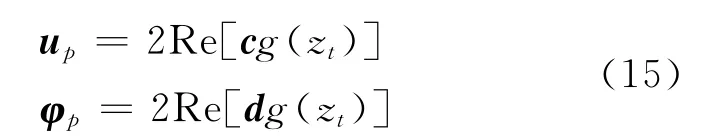
where c and d are the heat eigenvectors，which can be determined from the following equations

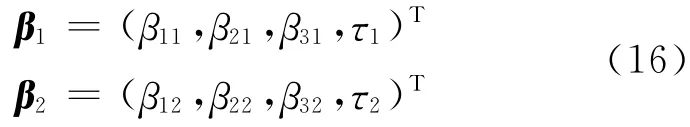
The final solutions of uandφare

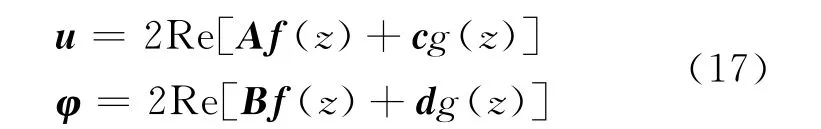
And Aand Bsatisfy the following orthogonality relation

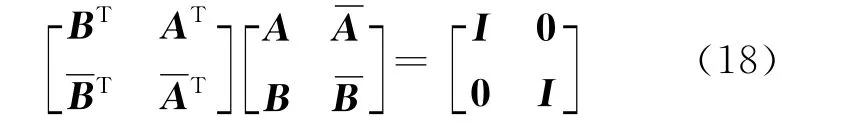
Assuming that the considered problem satisfies such a condition that for an arbitrary point on the boundary，the corresponding points ztand zα（α＝1－4）can be translated into an identical point，e.g.on the x1－axis or an unit circle，and as a result the boundary equation can be reduced to that containing one variable.Only under this condition，the one－complex－variable approach introduced by Suo［19］can be used to simplify analysis when the boundary conditions are considered［16，20］.In the present work these one－complex variable equations can be summarized as

Consider a generalized 2Dproblem of a thermopiezoelectric medium containing an circular hole as shown Fig.1.

The boundary conditions at the rim of the hole are

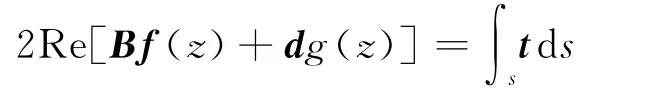
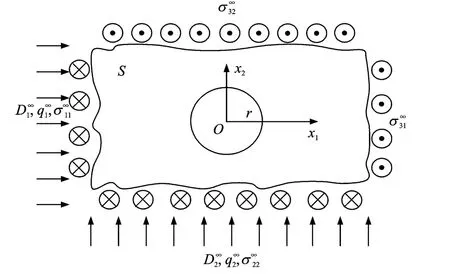
Fig.1 Circular hole in thermopiezoelectric solid

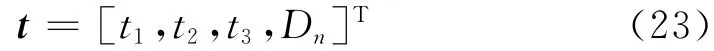
3 Temperature Field in Medium

From Eq.（9），the semi－permeable boundary conditions of heat flow is

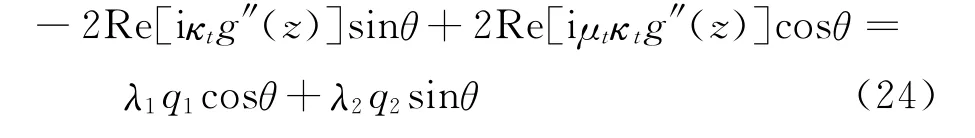
g′（z）takes the form of

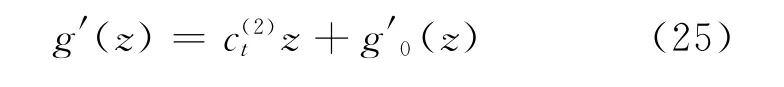
where g′0（z）is a holomorphic function outside the hole，g′0（∞）＝c（1）t，c（1）tis a constant corresponding to an uniform temperature field and thus can be neglected without loss in generality，andis another constant to be determined.

采用脱水剂，如DCC加速反应的机理是DCC上带孤对电子的N进攻羧基氢，获得氢后DCC中间C原子带正电，然后失去氢后的羧基氧负进攻DCC中间C，接着DMAP吡啶环上的N因为带有孤对电子，进攻羧基C，同时羧基另一个氧连在DCC上脱去，形成DCU，最后DMAP吡啶环上N进攻羟基氢，获得氢后离去，而失去氢的羟基氧负进攻羰基C并成酯。DCC参与反应，一般要过量，DMAP可视为催化剂。

Substituting Eq.（25）into Eqs.（20－21），and taking the limiting z→∞yields

Eqs.（26－27）give

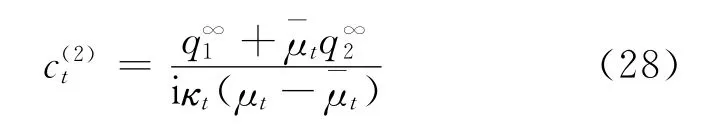
The following transform functions

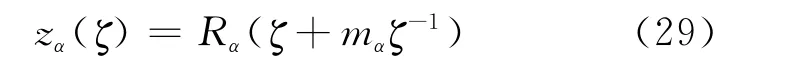
Noting that on the hole，ζ＝σ＝eiθ，and

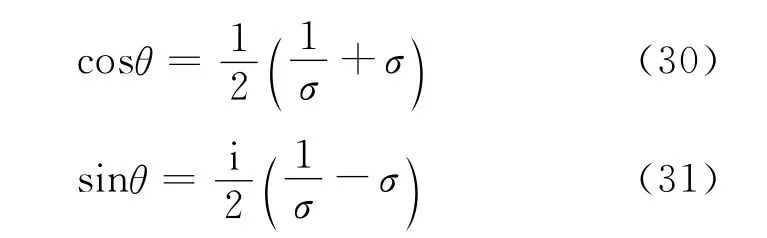
Eq.（24）can be rewriten as

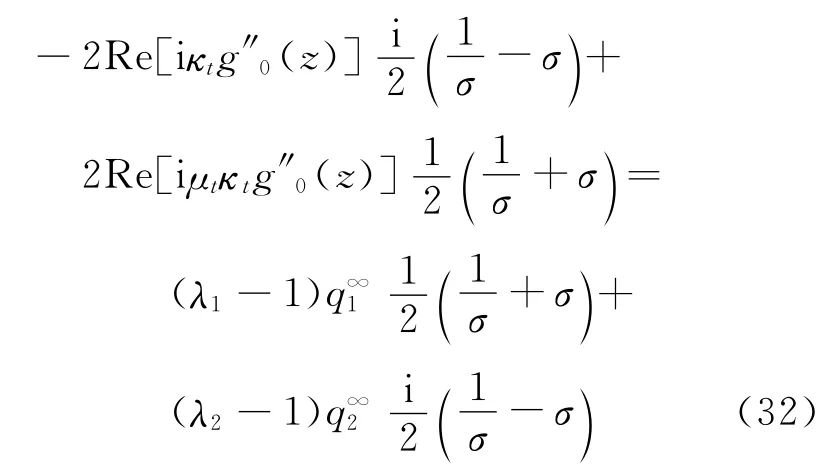
Calculating the Cauchy integration leads to

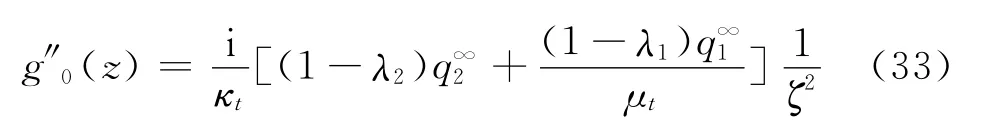
Therefore the final form of g″（z）can be ex－pressed as

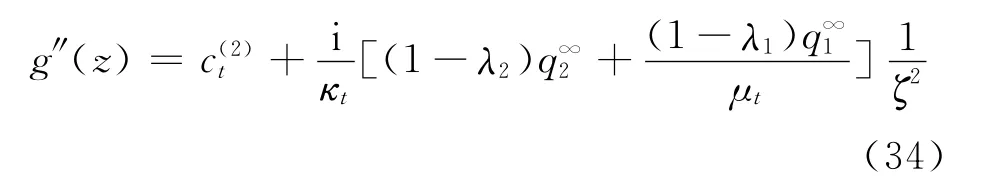
4 Electro－Elastic Field in Medium

Observing Eq.（36），the complex potential in the medium can be expressed as

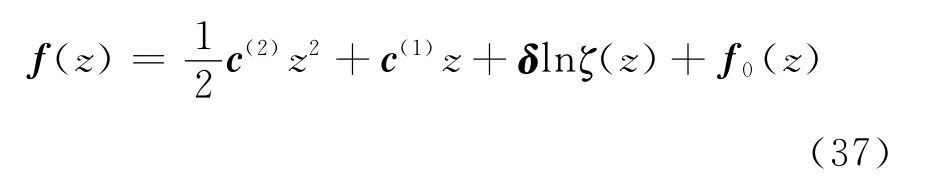
where f0（z）is a holomorphic function outside the hole；c（2），c（1）andδare the three constant vectors to be found.

The force equilibrium condition and the conditions of single－valued displacement and electric potential require

whereΓnstands for a clockwise closed－contour encircling the hole，and

Substituting Eq.（37）into Eqs.（39－40），and then using the residue theorem produces

Using Eq.（18）and Eqs.（41－42）yields

Considering the fact that both the stresses and strains are bounded at infinity，we have

Using Eq.（18）one obtains from Eqs.（44－45）that

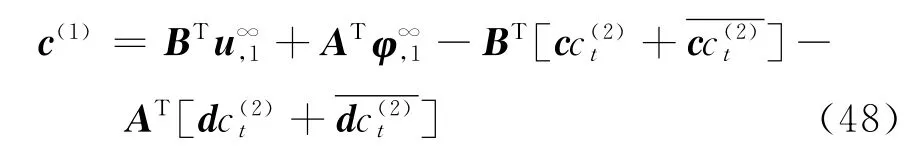
On the other hand，Eqs.（46－47）imply that the complex functions（）z and（Bc（2）＋）z，which are corresponding to the uniform heat flow in an infinite medium without holes，will not produce stress and strain，and thus can be cut out in the boundary equations.Thereforeφ and ucan be rewriten as

where

On the hole，we have

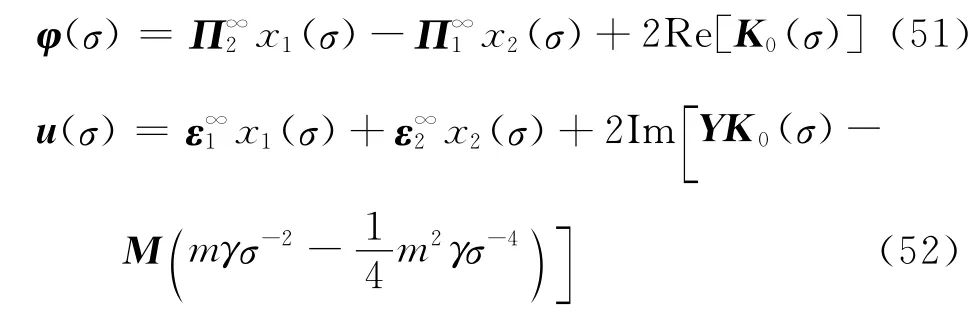
where

Ignore the electric field within the hole，the boundary condition is

Namely

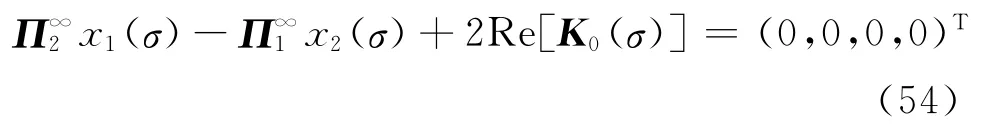
One can obtain after calculating the Cauchy integration that

So far，all the field variables can be calculated.

5 Stresses on Hole Rim

The stress components are

Consider a transversly isotropic piezoelectric medium cadmium selenide，where the poling direction is parallel to the X3－axis.The material constants are

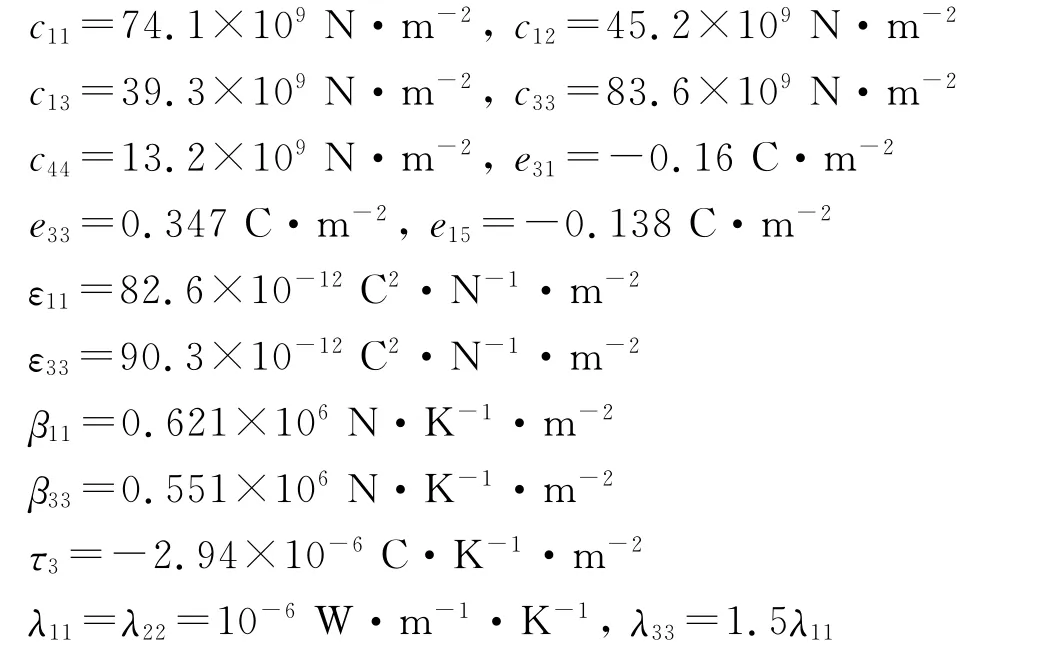
If our attention is focused on the field in X1－X3plane，the out－of plane displacement does not couple with the in－plane displacements and the electric potential，and the elastic matrices S，R and Wdegenerate into the 3×3ones

andβ1＝（β11，0，0）T，β2＝（0，β33，τ3）T.

Based on the given constants，we have

and

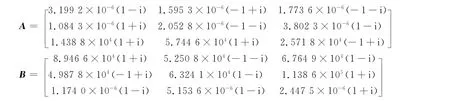
Fig.2shows the normalized hoop stress on the rim of holeλ22σφφ／10β11versus orientationθ with different value ofλ1at q∞1＝1W·m－2，r＝10－4m，λ2＝0.It is seen thatλ22σφφ／10β11reaches its maximum whenθ＝0andπ.The value of λ22σφφ／10β11equals to zero whenθ＝π／2orθ＝3π／2.The hoop stressλ22σφφ／10β11decreases with the increasement of the thermal conduction coefficient，which means if the heat flow may pass through the hole easily，the hoop stress around the hole will be low.On the contrary，the gathering heat flow enhances the hoop stress.

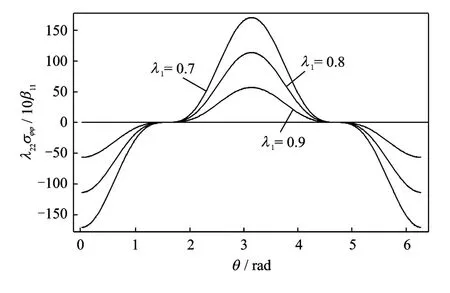
Fig.2 Curves for normalized hoop stressλ22σφφ／10β11 versus orientationθat ＝1W·m－2，r＝10－4 m，λ2＝0

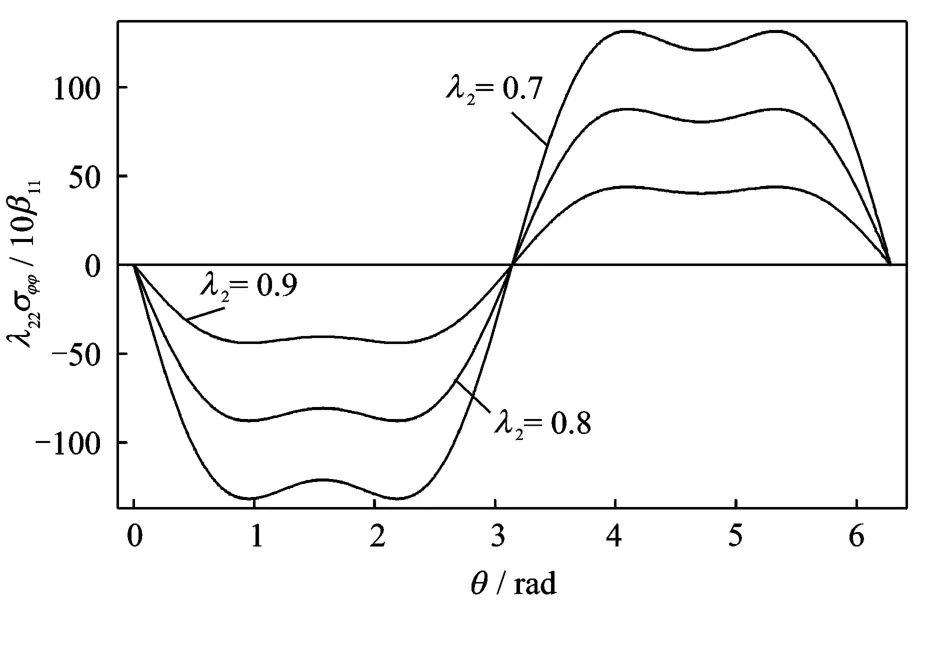
Fig.3 Curves for normalized hoop stressλ22σφφ／10β11 versus orientationθat q∞2＝1W·m－2，r＝10－4 m，λ1＝0

Fig.3shows the normalized hoop stress on the rim of holeλ22σφφ／10β11versus orientationθ with different value ofλ2at q∞2＝1W·m－2，r＝10－4m，λ1＝0.It is seen that the value ofλ22σφφ／10β11equals to zero whenθ＝0andθ＝π.Atθ＝1，2.4，4.14and 5.54，｜σφφ｜reaches its maximum.Whenθ＝π／2andθ＝3π／2，｜σφφ｜reaches its second largest value.

6 Heat Flow on Hole Rim

From Eqs.（20－21）we have

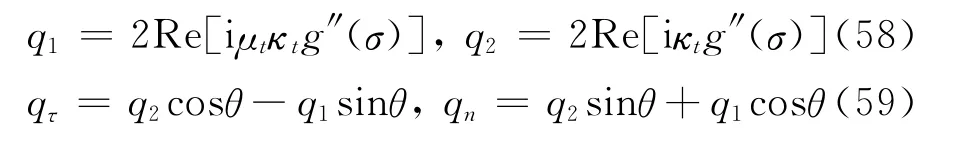
Fig.4shows the normal component of heat flowqnversus orientationθwith different value of λ2at q＝1W·m－2，r＝10－4m，λ1＝1.It is seen thatλ2has a significant influence on qn.The orientationθincreases with the increasement ofλ2when qnreaches its maximum，but whenθ＝0orθ＝π，qnandλ2are independent.

Fig.4 Curves for heat flowqnversus orientationθwith different value ofλ2at q＝1W·m－2，r＝10－4 m，λ1＝1

The curves for variations of heat flowqnversus orientationθwith different value ofλ1are shown in Fig.5for the case of＝1W·m－2，r＝10－4m andλ2＝1.The orientationθdecreases with the increasement ofλ1when qnreaches its maximum，but whenθ＝π／2orθ＝3π／2，qnandλ1are independent.

Fig.5 Curves for heat flowqnversus orientationθwith different value ofλ1at q∞1＝q∞2＝1W·m－2，r＝10－4 m，λ2＝1

The curves for variations of heat flowqτversus orientationθwith different value ofλ2are shown in Fig.6for the case of q∞1＝q∞2＝1W·m－2and r＝10－4m andλ1＝1.It is seen thatλ2has a significant influence on qτ.The orientationθ decreases with the increasement ofλ2when qτreaches its maximum，but whenθ＝π／2orθ＝3π／2，qτandλ2are independent.

Fig.6 Curves for heat flowqτversus orientationθwith different value ofλ2at q∞1＝q∞2＝1W·m－2，r＝10－4 m，λ1＝1

Fig.7shows the tangential component of heat flow qτversus orientationθwith different value ofλ1at q∞1＝q∞2＝1W·m－2，r＝10－4m andλ2＝1.It is seen that｜qτ｜decreases with the increasement ofλ1.And the orientationθincreases with the increasement ofλ1when qτreaches its maximum，but whenθ＝0orθ＝π，qτandλ1are independent.

Fig.7 Curves for heat flowqτversus orientationθwith different value ofλ1at q∞1＝q∞2＝1W·m－2，r＝10－4 m，λ2＝1

7 Conclusions

（1）The thermal boundary condition has significant effect influence on the hoop stress and heat flow around a hole in thermopiezoelectric materials under a thermal loading.

（2）The hoop stress decreases dramatically with the increasement of the thermal conduction coefficient，which means if the heat flow may pass through the hole easily，the hoop stress around the hole will be low.On the contrary，the gathering heat flow enhances the hoop stress.

（3）The orientationθwhen qn（or qτ）reaches its maximum changes with the variation of the thermal conduction coefficientλ1（andλ2）.But at certain points，qn（or qτ）andλ1（andλ2）are independent.

Acknowledgements

The work was supported by the National Natural Science Foundation of China（11232007，11202099）；the Foundamental Research Funds for the Central Universities of China（NS2012031）.

［1］ Florence A L，Goodier J N.Thermal stresses due to disturbance of uniform heat flow by an insulated ovaloid hole［J］.Journal Applied Mechanics，1960，27（4）：635－639.

［2］ Sih G C.On the singular character of thermal stresses near a crack tip［J］.Journal Applied Mechanics，1962，29（3）：587－589.

［3］ Parton V Z.Fracture mechanics of piezoelectric ma－terials［J］.Acta Astronaut，1976，3：671－683.

［4］ Zhang X Z，Hasebe N.Basic singular thermoelastic solutions for a crack［J］.Int J Fract，1993，62：97－118.

［5］ Chao C K，Shen M H.Explicit solutions for curvilinear cracks in the thermoelastic medium［J］.Journal of Thermal Stresses，1993，16（3）：215－231.

［6］ Chao C K，Shen M H.On bonded circular inclusions in plane thermoelasticity［J］.Journal Applied Mechanics，1997，64（4）：1000－1004.

［7］ Kattis M A，Patia A P.Thermal stress problem for a partly debonded rigid circular－arc fiber inclusion in an infinite matrix［J］.Engineering Fracture Mechanics，1994，48（3）：359－366.

［8］ Kaminskii A A，Flegantov L A.Temperature stresses around cracks in an elastic plate weakened by two holes［J］.International Applied Mechanics，1994，30（9）：707－712.

［9］ Sturla F A，Barber J R.Thermal stresses due to a plane crack in general anisotropic material［J］.Journal Applied Mechanics，1988，55：372－376.

［10］Hwu C.Thermal stresses in an anisotropic plate disturbed by an insulated elliptic hole or crack［J］.Journal Applied Mechanics，1990，57（4）：916－922.

［11］Hwu C.Thermoelastic interface crack problems in dissimilar anisotropic media［J］.International Journal Solids and Structures，1992，29（16）：2077－2090.

［12］Tarn J Q，Wang Y M.Thermal stresses in anisotropic bodies with a hole or a rigid inclusion［J］.Journal of Thermal Stresses，1993，16（4）：455－471.

［13］Chao C K，Chang R C.Thermoelastic problem of dissimilar anisotropic solids with a rigid line inclusion［J］.Journal Applied Mechanics，1994，61（4）：978－980.

［14］Lin S T，Feng Z，Rowlands R E.Thermoelastic determination of stress intensity factors in orthotropic composites using the J－integral［J］.Engineering Fracture Mechanics，1997，56（4）：579－592.

［15］Shen S，Kuang Z B.Interface crack in bi－piezothermoelastic media and the interaction with a point heat source［J］.International Journal Solids and Structures，1998，35（30）：3899－3915.

［16］Gao C F，Wang M Z.Collinear permeable cracks in thermopiezoelectric materials［J］.Mechanics of Materials，2001，33（1）：1－9.

［17］Gao C F，Zhou Y T，Wang M Z.An exact and explicit treatment of an elliptic hole problem inthermopiezoelectric media［J］.International Journal Solids and Structures，2002，39：2665－2685.

［18］Ueda S.The crack problem in piezoelectric strip under thermoelectric loading［J］.Journal of Thermal Stresses，2006，29（4）：295－316.

［19］Suo Zhigang.Singularities，interfaces and cracks in dissimilar anisotropic media［J］.Proc R Soc A，1990，427（1873）：331－358.

［20］Ting T C T.Common errors on mapping of nonelliptic curves in anisotropic elasticity［J］.Journal of Applied Mechanics，2000，67（4）：655－657.