麦克斯韦关系式的推导式记忆

宋谋胜，陈 琳

（ 铜仁学院 大数据学院，贵州 铜仁 554300 ）

麦克斯韦关系式的推导式记忆

宋谋胜*，陈 琳

（ 铜仁学院 大数据学院，贵州 铜仁 554300 ）

以热力学基本方程为基础，根据内能、焓、自由能和Gibbs函数等四个特性函数的物理定义式，并结合全微分、偏导数等数学方法，推导出了四对Maxwell关系式，有助于加深对该关系式的理解和识记。

麦克斯韦关系； 热力学函数； 推导记忆

由热力学基本关系推导的四对Maxwell关系，即麦氏关系，以简明的形式提供了实验不可测或难测的热力学量与实验可测量之间的关系，如体积膨胀系数、热容量等。由p、S、V、T四个热力学函数组成的八个两两对应的一阶偏导数，加之其括号外的角标，致使在实际教学中记忆麦氏关系较为困难。为了能记忆麦氏关系，人们曾提出了许多简单的记忆方法，如对角线法[1]、四方图法[2]、联相-交换法[3]等。另外，一些学者还将Jacobi行列式用于麦氏关系的推导和记忆[4,5]，取得了较好的效果。

为了帮助初学者掌握和记忆麦氏关系，笔者根据多年的教学实践，提出了利用热力学基本函数的物理意义表达式和公式的数学推导相结合的推导式记忆法，即一个基础（热力学基本微分方程）、四个热力学特性函数物理表达式（U、H、F、G）、三种数学方法（全微分、一阶偏导数、二阶偏导数）。该方法关键在于热力学基本关系的物理意义与数学意义上的全微分偏导数的结合，重在理解性推导，能帮助初学者通过理解推导而记忆麦氏关系。

1.麦氏关系的推导基础

麦氏关系是从内能（U）、焓（H）、自由能（F）和Gibbs函数（G）四个热力学特性函数的数学推演而得出的。根据物态方程、内能和熵可导出热力学基本微分方程

dU=TdS-pdV （1）

该方程又称热力学第一定律，给出了两个平衡态的内能、熵和体积之间的关系[6]，是麦氏关系的推导基础。现以（1）式为基础，根据内能、焓、自由能和Gibbs函数的物理定义式，并结合全微分和偏导数来分别推导四对麦氏关系。

2.麦氏关系的推导

2.1.由内能函数（U）来推导

由热力学基本微分方程（1）式可知，dU与变量dS、dV相关，即U与S、V有关，则U作为S、V的函数，有U=U( S, V)，其全微分为

将方程（1）和（2）比较可得

由于U是S、V的连续函数，将（3）式左边分别对V、S求二阶导数，右边分别对V、S求一阶导数。

近年来，国家开始重视产教融合，特别是产教融合平台的建立，初步搭建了产业与教育融通的渠道。各地方院校也纷纷推出产教融合的新举措，拓宽了产教融合的渠道。尤其是在职业教育与产业对接、人才培养模式等方面成效显著。

（4）式即为根据内能的物理意义结合数学的全微分偏导数而推导出的麦氏关系之一。

2.2.由焓函数（H）来推导

热力学焓函数（H）的物理定义为H=U+pV ，其全微分为

将热力学基本微分方程（1）式代入，可得

可见，dH与变量dS、dp相关，则H作为S、p的函数，有H=H( S, p)，其全微分为

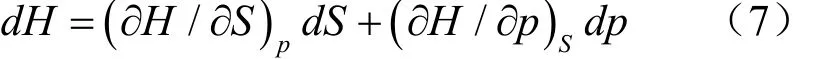
比较方程（6）和（7），可得对应关系

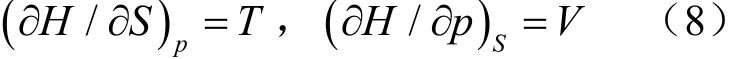
由于H是S、p的连续函数，将（8）式左边分别对p、S求二阶导数、右边分别对p、S求一阶导数。根据连续函数求二阶导数可交换求导次序，可得（9）式即为根据焓的物理定义和数学的全微分偏导数而推导出的麦氏关系之二。

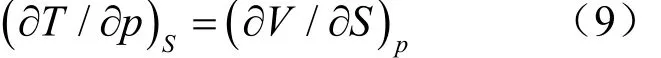
热力学自由能函数（F）的物理定义为F=U-TS，其全微分为

将热力学基本微分方程（1）式代入，可得

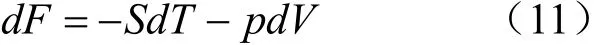
可以看出dF与变量dT、dV相关，则F作为T、 V的函数，有F=F( T, V)，其全微分为

比较方程（11）和（12），可得对应关系

将（13）式左、右两边分别对V、T求二阶、一阶导数，根据∂2F/(∂T∂ V)=∂2F/(∂V∂ T)，可得这就是根据自由能的物理定义和及其数学上全微分偏导数而推导出的麦氏关系之三。

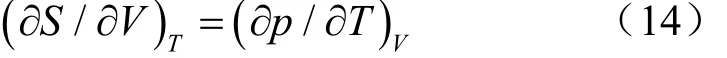
2.4.由Gibbs函数（G）来推导

Gibbs函数（G）的物理定义为G=U-TS+pV ，其全微分为

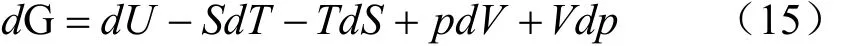
将热力学基本微分方程（1）式代入，可得

可见dG与变量dT、dp相关，则G作为T、p的函数，有G=G( T, p)，其全微分为

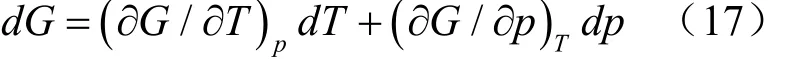
比较（16）（17），可得对应关系

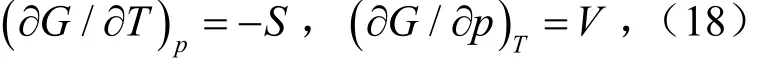
将（18）式左、右两边分别对p、T求二阶、一阶导数，根据∂2G/(∂T∂ p)=∂2G/(∂p∂ T)，可得

（19）式即为根据Gibbs函数的物理定义和及其数学全微分偏导数而推导出的麦氏关系之四。

3.结论

以热力学基本微分方程为基础，数理结合，根据内能、焓、自由能和Gibbs函数等四个热力学特性函数的物理定义，并结合该类函数的数学分析方法，推导出了四对Maxwell关系式。

[1] 韩雪峰.麦克斯韦关系的规律记忆法[J].廊坊师专学报（自然科学版），1997，（3）：30-31.

[2] 路莹.热力学关系和麦克斯韦关系的教学研究[J].洛阳师范学院学报，2003，（2）：25-26.

[3] 曹海静，田冰涛.热力学麦克斯韦关系的简便记忆方法[J].科技资讯，2012，（21）：203.

[4] 陈沙鸥，吴哲英，李岩.麦克斯韦关系的矩阵方法推导[J].青岛大学学报，2000，13（3）：1-5.

[5] 邱敏，牟艳男，张秀平.雅克比行列式与麦克斯韦关系有机结合的探讨[J].黑河学院学报，2010，1（3）：114-116.

[6] 汪志诚.热力学·统计物理[M].北京：高等教育出版社，2008.

Derived memory of Maxwellian relations

SONG Mousheng, CHEN Lin
(School of Data Sciences, Tongren University, Tongren, Guizhou 554300, China )

Based on the thermodynamic basic equation, according to the physical definitions of four characteristic functions including internal energy, enthalpy, free energy and Gibbs function, and combining with the total differential, partial derivative, etc. mathematical methods, four Maxwellian relations were derived. It is contributed to enhance the understanding and memory of those relations.

Maxwellian relation, thermodynamic function, derived memory

O551

A

1673-9639 (2016) 04-0044-03

（责任编辑 佘彦超）（责任校对 毛 志）

2016-02-17

贵州省物理学专业综合改革试点项目（黔财拨[2012]207）。

宋谋胜（1972-），男，湖南怀化人，教授，博士，研究方向：大学物理教学与研究。

*通讯作者：宋谋胜，E-mail：sms071201@163.com。