隧道洞内平面控制网形与数据处理方法实验研究

2016-12-06李学仕王靠省

铁道勘察 2016年5期

关键词：抗差边角方位

李学仕周适王靠省郭平

(中铁二局集团有限公司，四川成都 610031)

隧道洞内平面控制网形与数据处理方法实验研究

李学仕周适王靠省郭平

(中铁二局集团有限公司，四川成都 610031)

建立地面实验网，用GNSS测量结果作为参考值，对交叉导线网、横控交叉网、菱形交叉网和中间自由测站点对网等网形进行同步实测，对各种网形就距离定权、距离角度方差估计、常规平差与稳健估计、加入不同精度的陀螺方位等进行测试计算，分析不同方法与处理参数对控制网横向贯通误差的影响。为提高隧道洞内平面控制网的贯通精度及可靠性，应尽量减少旁折光的影响，宜采用交叉导线网或中间自由测站的边角交会网形；有条件时应测量高精度的陀螺方位边，采用边角匹配抗差平差方法处理控制网数据。

隧道洞内平面控制网距离误差边角定权抗差平差高精度陀螺方位

隧道洞内空间狭小，平面测量控制网一般采用精密导线形式。随着光电测距技术与全站仪设备的发展，历经了单导线、主副导线、双导线网、菱形交叉导线网等多种形式[1]，长隧道一般采用双导线环网和菱形交叉导线网[1-3]。利用高精度自动测量机器人，借鉴高速铁路轨道控制网CPIII的网形[2]，逐步形成了中间自由测站边角交会的点对网形式[4]。这些控制网均测量点间角度、距离，统称为边角网。长隧道的边角网还可用加测高精度陀螺方位的方法来提高贯通精度[1-3，5，6]。隧道洞内边角网有多种不同数据处理方式和方法，包括距离的不同定权[2，7，8]、边角方差估计[8，9]、稳健估计(抗差平差)[10]等。由于控制网在地下，这些网形和数据处理方法计算结果的正确性与真实性很难得到客观确认，在工程实际应用中还带有一定的盲目性与试探性。

本课题针对铁路长隧道洞内平面控制网测量，研究前述几种网形的优缺点，分析距离定权方法、边角定权方法、常规定权和赫尔默特方差估计方法对平差结果的影响，并实地建立一个长度约8 km的地面模拟实验网，用GNSS测量结果作为参照，测量交叉导线(网形1)、加测横距的横控交叉导线(网形2)、菱形交叉双导线(网形3)以及中间自由测站的边角交会点对网(网形Z)等4种形式的控制网数据，分析验证不同形式控制网的精度与可靠性；拟找到长大隧道洞内控制网贯通精度最高的可靠网形及其数据处理技术方法(如图1)。

1 实验网介绍

1.1 网布设形式与观测

实验网选在平原上一段暂停施工的铁路高架桥上，该段桥梁处于东西方向，大部分为直线，西端有一小段位于曲线上；从170号到455号墩，每跨32.7 m，总长度约为9.2 km。根据实验网技术方案，沿桥梁纵向每10跨(约为327 m)在桥墩处梁面上布设点对(即左右布设的两个测量点)，点对(共计26对)的横向距离为4～6 m。测量标志采用徕卡反射片，用胶粘贴在梁面上。

在控制网两端及每1/4处选择左右交错的3个点进行GNSS测量，作为与边角网测量对比的参考点。从东到西分成连续独立的4小段(分别为A、B、C、D段)，从头到尾全部控制点为整段(为E段)，从两端向中间贯通段(为G段)。其中A、B、C、D、E段均为GNSS独立测量，作为各段计算的起算数据。为测试陀螺方位作用，将这些独立测量GNSS数据整体处理，得到全网综合数据。

每段网均分为4种网形：交叉导线(网形1)、加测点对横距的交叉导线(网形2)、交叉菱形双导线(网形3)以及中间设站的边角交会点对网(网形Z)，如图1。为便于闭合检核，在网形1中每隔2点设闭合点形成6条边的闭合环。网形2是在网形1基础上观测点对的短横距。

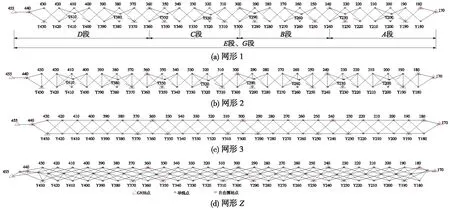
图1 实验网形与分段

为进行网形比较，测量时将各种网形观测同步推进，尽量减少重新对中整平。网形Z不在控制点上设测站，只观测前后各4个控制点，先行观测后再到控制点上设站观测前后相邻控制点；将网形1、网形2与网形3综合在一起观测，数据处理时抽取各自网形的观测数据。

实验网的参考点采用二等精度的GNSS测量，边角测量为二等网精度，采用经检定的Leica TCA2003与配套圆棱镜施测，方向观测6测回，往返测量距离和天顶距各1～2测回；测量数据用电子手簿自动采集。

1.2 实验网数据处理结果

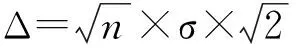
GNSS网不同时段独立观测的重复边距离较差最大3.3mm，方位较差最大1.9″。边角网的距离观测值往返较差均小于3mm，用往返较差计算的测距中误差为0.89mm；26条点对横距往返较差最大1.0mm，中位数0.4mm。由网形3检查的51个四边形角度闭合差均小于4″，根据角度闭合差计算的测角中误差为0.97″；由网形1计算的9个六边形和16个四边形计算的测角中误差为0.63″；所有坐标和全长闭合差均满足按距离、角度误差计算的限差要求。

边角网与GNSS网的距离较差最大为2.2mm；实测角度与GNSS网独立测量的角度比较最大较差为3.1″，GNSS角度取均值后最大较差为1.9″。GNSS与全站仪测量均包含了对点误差，当对中误差在0.5mm、前后视距离为320m时，前后视对中误差对方位误差的影响为0.32″，棱镜与仪器对中误差综合影响角度误差[2]为0.51″。可见对中误差对中短距离的方位或角度的影响不能忽略。

1.3 测试内容与计算方法

实验网以计算各种控制网形终点的横向摆动量(横向贯通误差)和终边方位误差为目标，比选出横向误差最小的网形结果。

每种网形按以下参数和方法计算。

(2)边角权比协调：按先验精度定权常规平差计算，以验后方差估计重新定权协调距离方向的权比，即赫尔默特方差估计方法平差。

(3)稳健估计测试：对含有粗差的观测值自动进行降权处理，即抗差平差。

(4)对于整网(E网形)，将中部的GNSS方位作为陀螺方位观测值进行测试计算。

2 结果分析

2.1 距离定权

网平差中，距离定权随其误差计算方式而不同，有

(1)

(2)

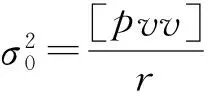
实验网计算结果显示，两种距离定权方式平差后横向坐标的差异很少超过1mm，表明在这种直伸控制网形中，距离定权方式差异对横向坐标的影响不明显。

另外，对网形2中的26条横控短距赋以0.5mm的误差参与平差，在较长的E段网中才体现出对横向坐标略微有影响，其它短网中影响极小。

2.2 距离角度权比协调

常规边角网平差中，以方向观测值先验误差为单位权中误差，一般不区分各方向点，所有方向观测值定权均为1[7]

(3)

距离观测值一般定权为

(4)

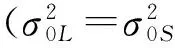
由测试网计算结果可知，采用常规边角定权方法与边角匹配(赫尔默特方差估计)方法平差的结果，横向坐标差异最大1.8 mm(8.4 km长的E网)，对于这种直线隧道洞内狭长控制网的横向坐标影响很微小，其差异不显著。直观上分析，这是因为相对于测角误差来说，直伸导线中测距误差对横向误差的影响要小得多的缘故。

2.3 抗差处理

控制网经过各种质量检查后再参与平差，但观测值中可能仍然含有粗差。抗差(稳健)估计[10]的基本思想是：在粗差不可避免的情况下，在预平差后对观测值的改正数采用适当方案进行检查判断，对识别出的粗差观测值降权，再进行平差处理，使平差结果尽可能避免粗差的影响。目前常用的权调整方案[10]主要有等价方差-协方差法、丹麦法、Huber法、IGG法等。

对实验网的A、B、C、D、E、G段的网形1、2、3、Z分别采用常规平差、常规抗差、匹配平差与匹配抗差处理，其中抗差方案为Huber法，横坐标变化最大值如表1所示。

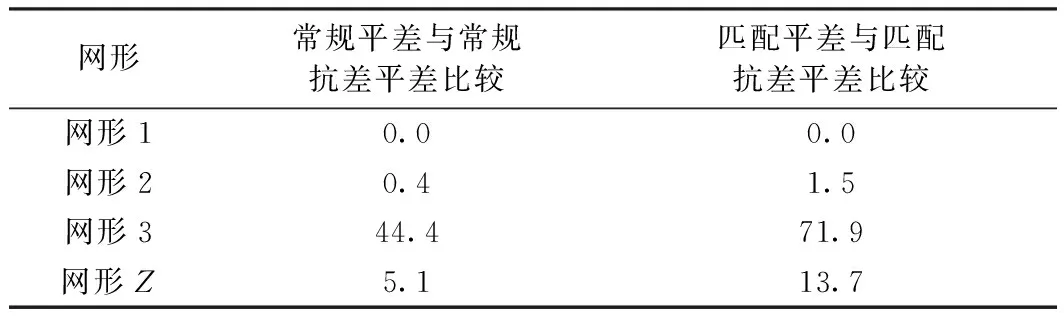
表1 不同方法平差结果的最大差异 mm

实验网计算数据表明：

(1)不管是常规抗差还是边角匹配抗差，网形Z、网形3的计算结果变化显著，网形1、网形2差异不显著；这是因为有较多的多余观测数才能准确识别出大误差。

(2)常规抗差和边角匹配抗差平差计算的网形Z、网形3，都使得贯通误差更小。因此，抗差处理对未搜索到的大误差有很好的规避效果。

(3)采用匹配抗差处理得到的贯通误差最小。

采用抗差平差的方法能起到自动纠偏的作用，配合边角匹配的定权方式，可提高贯通精度。因此，隧道洞内平面控制网的数据处理，采用边角匹配的抗差平差方法效果最佳。

2.4 网形比较

采用匹配抗差处理各段的各种网形，得出的贯通误差如表2所示。

实验网计算数据显示：

(1)网形Z的贯通误差大多数情况下是最小。

(2)网形1、网形2，贯通误差很接近，有时贯通精度比网形Z高。

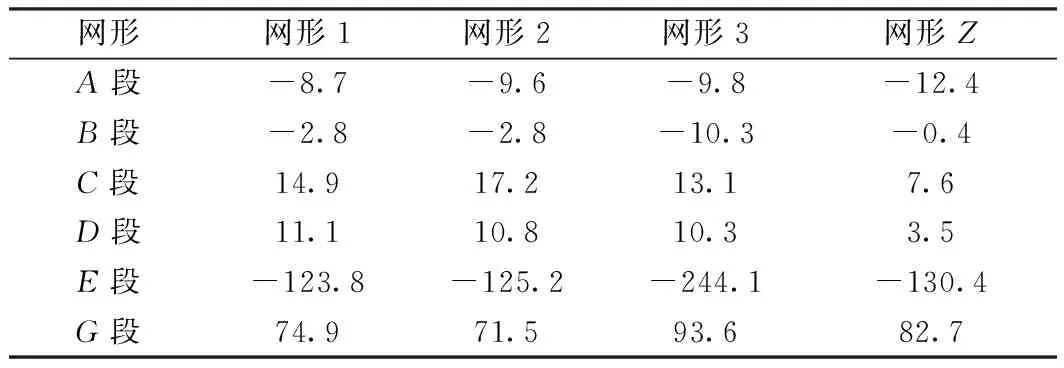
表2 不同网形的贯通误差 mm

(3)网形3的贯通误差在短网中有高有低，长网形中贯通误差最大。

对全长贯通的E段各种网形数据进行首尾约束贯通平差，得出沿途控制点坐标。平差结果显示，每种网形采用常规平差、边角匹配平差、匹配抗差处理的坐标结果差异不大；边角匹配抗差结果与GNSS坐标的差异最小，如图2所示。

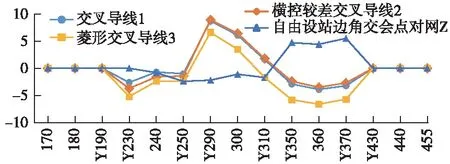
图2 按边角匹配抗差平差的横向贯通坐标与GNSS坐标的差异(单位：mm)

图2中显示，各种网形贯通平差后的坐标都接近GNSS坐标，自由测站边角交会点对更加可靠。

分析认为：

(1)经验与测试结果都表明，网形3的多余观测数虽然多，但其网形中靠近且平行于洞壁的方向易受到旁折光影响(实验网是受到桥梁上的纵向挡渣墙旁折光影响)，无法采用数据处理的方法予以消除，贯通精度还受到仪器、棱镜对中误差的影响。

(2)网形2与网形1，由于旁折光影响减小，贯通误差要网形3要小。在没有强制对中时存在仪器、棱镜对中误差的影响。如果采用强制对中，这种网形相对于网形Z来说，观测量少，贯通精度也高。

(3)网形Z避免了仪器对中误差，同时避免了旁折光影响，多余观测数最多，具有较强的抗差能力，因而这种网形的贯通精度高、贯通结果可靠。

2.5 高精度陀螺方位的影响

理论上，为提高直伸导线贯通精度，加测一个陀螺方位角时，以加测到支导线全长2/3处(0.69～0.74倍)为最优[1，3，5]。考虑到陀螺仪测量系统本身的测量误差和测量时的仪器对中安置误差，从已知方位边引测到未知方位边的陀螺方位相对于起算数据是含有误差的。从误差大小来看，只有陀螺方位精度远远高于导线测量的方位累计误差时，才可以忽略陀螺方位的误差。因此，陀螺方位角参与网平差时，一般宜作为带有误差的方位观测值[9]。

实验网E段数据在各网形全长2/3位置Y350～360边施加陀螺方位边观测，陀螺方位值取GNSS测量的方位。忽略GNSS方位误差，导线测量按1.0″测角精度且按双导线计，则导线方位与陀螺方位的较差限差为

网形1、网形2、网形Z的方位闭合差在5.0″左右，而网形3的方位闭合差达9.9″，应该是受到外界影响而超限。

起算数据采用全网综合数据，陀螺方位观测值分别按0″、1.0″、3.0″、5.0″的精度，用边角匹配平差方法处理，平差后终点455的坐标与GNSS坐标比较差值如表3。