主元分析的振动频域特征识别与磨机负荷建模研究
2016-12-06刘志刚蔡改贫林龙飞
刘志刚,蔡改贫,林龙飞,熊 洋
(江西理工大学 机电工程学院,江西 赣州 341000)
磨矿是选矿生产流程中一个十分重要的环节[1],是将矿石碎磨至有用矿物基本单体解离的细度,再经过分级后选别,磨矿工序产品质量的好坏直接关系选厂的经济和技术指标。磨矿过程是选矿生产中的能耗大户,通常该工序成本占总生产费用的40%~60%。因此,科学、准确地预测磨机内部运行状态及开发磨矿优化控制技术是选矿行业实现节能降耗、提质提产的根本任务之一[2]。
国内矿山冶金企业在磨矿过程的实际生产中一般是由现场技术人员通过振动产生的噪声、压力或有功功率等间接方法[3-5],对球磨机内部运行状态进行判断与处理,而基于人工操作主观判断具有很大的局限性,且误差较大。因此,能够准确反映磨机内部运行状态并影响磨矿过程产品质量及产量的磨机内部运行状态参数的测量,逐渐成为研究的热点[6-7]。王泽红等[8]提出采用正交试验法和多因素联合分析方法,建立了磨机负荷参数与振声、有功功率、荷重信号之间关系的预测模型;李勇等[6-7]采用灰色理论和RBF神经网络,建立了介质充填率与振声、轴承应变、功率信号之间的数学模型。在对磨机外部相应分析中,上述方法均未对振声信号的频谱进行谱估计或相关分析[6],而研究表明,磨机内负荷参数与振声信号的特征频段的功率谱能量值有关。近年来,基于球磨机外部响应振动信号进行球磨机内部状态参数预报的方法越来越受到关注[9]。因此研究提出基于主元分析(PCA)的振动频域特征识别和支持向量机的磨机负荷建模研究。
1 振动与负荷的关联
球磨机运行时,衬板将钢球带起,落下的钢球与物料层、其他钢球、衬板以及筒壁发生碰撞。钢球的一部分能量被物料层吸收,实现物料的破碎和研磨过程;钢球的另一部分能量消耗在钢球之间的碰撞摩擦以及钢球与衬板的碰撞摩擦,这一部分的能量释放导致了滚筒的振动,并沿着筒体和轴承传播,因此在球磨机的轴承或者滚筒上即可测出球磨机滚筒的振动信号。
由于筒内的物料层直接参与了钢球的能量分配过程,形象地说物料层就像厚度不断变化的海绵,吸收的能量也相应发生变化,所以轴承或滚筒振动的频谱与筒内物料负荷之间存在一定的对应关系。存料量不同,振动幅度不同,振动频谱中识别的与存料量相关的特征量也不同。因此,对振动信号进行适当的处理,就能有效地反映球磨机筒内的负荷。
2 频域特征识别与负荷建模
2.1 Welch功率谱估计
Welch算法是对周期图法的修正算法[10],其谱估计是将原长度为N的数据样本分成K段,每段长度为M=N/K,数据进行分段加窗先分别求出各个数据段的谱估计,再进行总平均。分段后数据相互独立,估计的方差减小为原来的1/K,达到一致估计。若K增大,M减小,则分辨率减小,若K减小,M增大,分辨率增大,则估计方差增大。在实际应用中应适当选取K和M值。其中各分段信号功率谱为式(1):

式中:XN(m)为输入信号函数。
将各段功率谱相加再进行总平均后为式(2):
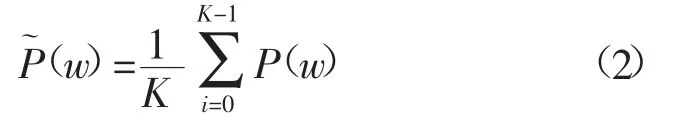
2.2 主元分析(PCA)
主元分析是将有一定相依关系的m个参数的n个样本值所构成的数据阵列,通过建立较小数目的综合变量,使其更集中反映原来m个参数中所包含的变化信息[11]。
假设[x1,x2,…,xP]为样本数据,用xi表示输入向量,相应的映射为φ,将向量xi进行标准化后,对其进行映射为φ的非线性变换,得到相关系数矩阵A为:
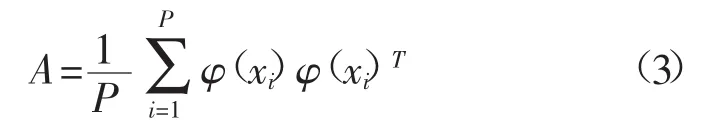
式中:P为样本数据个数。
通过求解矩阵A的特征值来确定具有高度相关性的指标,即主元。如式(4)所示。

式中:λ为相关系数矩阵的特征值,ν为特征向量。
取特征向量的分量值为权数,将标准化的指标进行加权得到第j主元见式(5)。

相关矩阵A的特征值等于对应主元的方差,其大小反映了第j个主成分所包含原始数据的全部信息比重,也反映了各主元贡献的大小。定义第j个主元的贡献率见式(6)。

方差贡献率αj越大反映其包含样本数据xi的信息能力越强。由此可将高维的信息空间进行降维,达到建立较小数目的综合变量,使其更集中反映原来m个参数中所包含的变化信息的目的。
2.3 支持向量机理论
支持向量机(Support Vector Machine,SVM)方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以期获得最好的推广能力[12]。
SVM主要思想是建立一个超平面作为决策曲面,使得待分样本之间的间隔最大化,并实现将分类问题转化为一个带约束的最值问题,如式(7)所示。

s.t.yi(
其中
令g(x)=
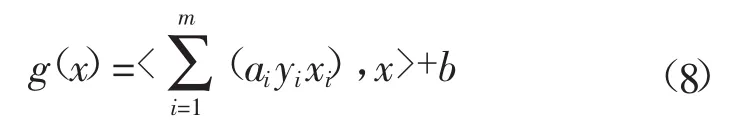
式中:x为变量,xi为已知样本向量,ai为拉格朗日算子。
将式(8)常量提出可得式(9):
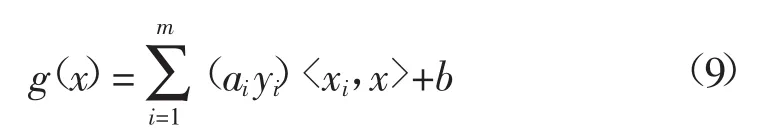
为使样本线性可分,引入核函数样本向量,其可将低维空间向高维空间转化。令f(x')=
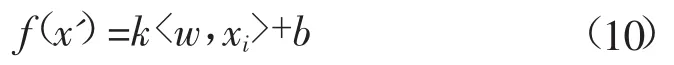
式k

为解决在实际使用核函数向高维空间映射后,数据样本仍然不可分的问题引入松弛变量ζ,松弛变量使SVM在样本分类具有容错能力[13];为了防止分类器由于分隔少量离散点而使得目标‖w‖变小的问题,引入惩罚因子C,使得分类器达到最优化分类[14]。经过变换,目标函数及其约束变换为式(12)。

s.t.yi(k
通过推导可知,原属于非线性分类问题转化为高维特征空间的线性优化问题,从而实现数据样本的分类。
2.4 磨机负荷模型的建立
(1)将采集的振动信号进行去噪预处理,采用Welch进行功率谱估计,得到振动信号的功率谱;
(2)按照一定的频带宽度将振动数据样本细等分为若干等份,并对各分频段的能量谱求和,得到各频段的能量值;
(3)将各频段能量值作为样本向量进行主元分析,将高维的数据样本向低维空间转化,得到降维后的样本矩阵;
(4)从主元分析得到的低维样本矩阵作为支持向量机的输入,相对应的负荷参数作为支持向量机输出,建立磨机负荷参数的预测模型。

图1 试验球磨机Fig.1 Experimental ball mill

图2 DH5922N动态数据采集仪Fig.2 DH5922N dynamic data logger

表1 入料粒度及钢球级配Tab.1 Feed size and ball grading
3 球磨机负荷参数试验结果
3.1 振动频谱与负荷参数分析
试验中取不同负荷进行振动采样,共分六组进行试验,每组负荷参数采取五个数据样本作为其标称信号,以负荷参数填充率30%、料球比0.6为例,其负荷参数的振动频谱如图3所示。
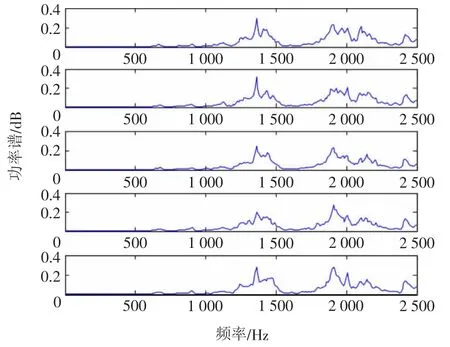
图3 负荷数据样本振动频谱图Fig.3 Vibration spectrum for load data samples
从5个数据样本的Welch法估计振动信号的功率谱图来看,其重复性很好,说明采取5个数据样本作为每组负荷参数的标称信号,利用其作为支持向量机的输入样本信号的科学性,其他负荷参数的功率谱估计具有相似特性。
将不同负荷参数下采集的振动信号,利用Welch法对同种负荷参数下的五个振动数据样本进行功率谱估计,振动信号和其功率谱能量值如图4所示。
由图3可知,对应不同的负荷参数,振动信号的功率谱能量值也不相同,信号的频谱能量值主要集中在2 500 Hz以下,并随着磨机负荷参数的变化,各信号频段的功率谱能量值将相应变化,再次说明磨机的负荷与振动信号各频段的能量值之间存在一定关系。如图4所示,当负荷参数为空载时,频率段在500 Hz以下的部分能量值,主要是磨机本身的固有振动频率,其他频段几乎为0;随着负荷参数中钢球数量越来越多,其对应的时域振动信号越密集,相应的功率谱能量值幅值越大;图4(e)所示,当负荷参数中加入物料后,其功率谱能量值下降,这也进一步解释在球磨机磨矿作业时钢球的一部分能量消耗在与衬板之间碰撞产生振动,另一部分参与物料的破碎过程。

图4 不同负荷参数下采集的振动信号及其Welch法估计振动信号的功率谱Fig.4 The acquisition of vibration signals and power spectrum for estimate vibration signal by Welch method under different load parameters
3.2 负荷参数预报模型
根据上面试验分析结果,磨机的负荷与振动信号频段500~2 500 Hz的能量值相关,将500~2 500 Hz的频段等分为25份,即各分频段的带宽为80 Hz,将各分频段的能量谱值求和,得到各频段的能量值,即得到25×25的输入矩阵样本。再将每个负荷参数对应的五个数据样本各频段能量值进行主元分析,降维得到25×4的样本矩阵,将其作为支持向量机的输入数据样本。支持向量机采用C-SVC模型,核函数为径向基核函数(RBF),20组为训练样本,另外5组为测试样本。训练样本和预测结果如表2、表3所示。

表2 训练样本归一化结果Tab.2 Normalized results of training samples
分别对训练数据、测试数据进行归一化处理,将训练得到的模型,利用测试样本对其进行预测验证。分别利用BP神经网络和支持向量机对样本数据建模、预测,对上述五种负荷的分类识别如表3所示,支持向量机可达到100%的分类预报准确率,且高于BP神经网络分类预测的效果。
4 结论
研究通过设计试验,采集磨机在不同负荷下的振动信号,对振动信号与球磨机负荷参数的相关性进行了研究,得到以下结论:
(1)通过对不同负荷参数下振动信号的功率谱估计,发现负荷参数中钢球与球磨机的振动信号相关性很高,并随着钢球的增多其振动的功率谱能量值逐渐增大;当磨机内加入一定量物料时,振动的能量值减小,是因为钢球抛落的部分能量值被矿石吸收参与磨矿。
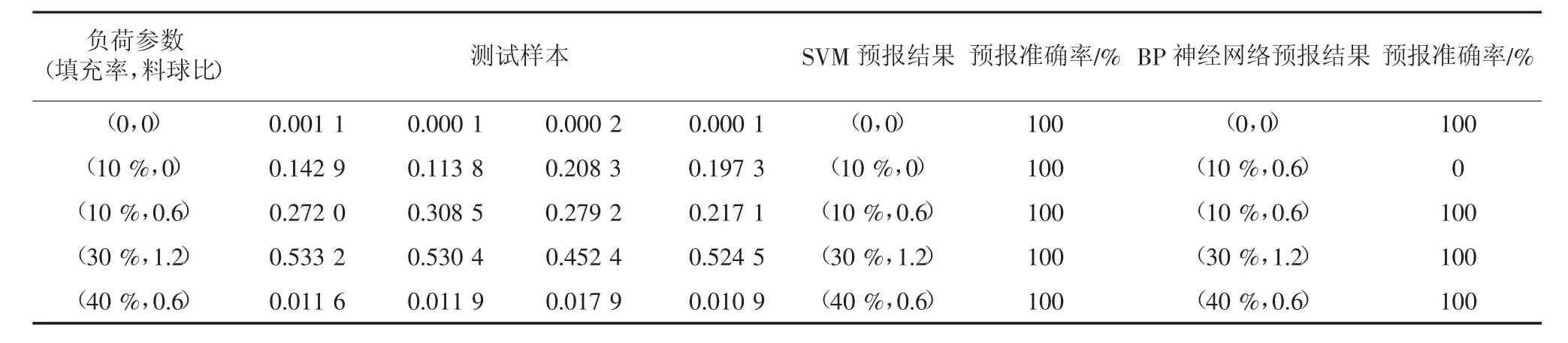
表3 负荷参数预报结果Tab.3 Forecasting results for load parameters
(2)利用磨矿过程产生的振动信号,采用Welch法对其进行功率谱估计,并提取信号的特征频谱段的能量值,分析发现振动信号功率谱与磨机筒体内负荷相关性大,然后采用主元分析法(PCA),对振动谱能量值进行降维,得到与负荷高度相关的谱能量成分,为复杂信号的分析与数据的挖掘提供一种思路。
(3)采用支持向量机(SVM)建立磨机负荷参数预报模型,实现磨机负荷参数(填充率、料球比)的分类预报。该方法可以准确预测磨机筒体内负荷,且比BP神经网络达到更准确的预报结果,为进一步研究磨机负荷检测提供指导。
[1]石 立,张国旺,肖 骁.金属矿山选矿厂磨矿分级自动控制研究现状[J].有色金属(选矿部分),2013(增刊 1):44-48.
SHI Li,ZHANG Guowang,XIAO Xiao.Research on automatic control of grinding and classification in concentration plants of metal mines[J].Nonferrous Metals(Mineral Processing Section),2013(supply1):44-48.
[2]蔡改贫,许 琴,熊 洋,等.球磨机磨矿系统多变量辨识建模的研究[J].中国钨业,2015,30(5):68-72.
CAI Gaipin,XU Qin,XIONG Yang,et al.Multivariable system identification modeling of ball mill grinding systems[J].China Tungsten Industry,2015,30(5):68-72.
[3]汤 健,郑秀萍,赵立杰,等.基于频域特征提取与信息融合的磨机负荷软测量[J].仪器仪表学报,2010,31(10):2161-2167.
TANG Jian,ZHENG Xiuping,ZHAO Lijie,et al.Soft sensing of mill load based on frequency domain feature extraction and information fusion[J].Chinese Journal of Scientific Instrument,2010,31(10):2161-2167.
[4]BHAUMIK A,SIL J,BANERJEE S.Designing of intelligent expert control system using petri net for grinding mill operation[J].Wseas Transactions on Information Science and Applications,2005,4(2):360-365.
[5]NIERO PM A V,MOYSM H.Exploration of mill power modeled as function of load behaviour[J].Minerals Engineering,2001,14(10):1267-1276.
[6]李 勇,邵 诚.灰色软测量在介质填充率检测中的应用研究[J].中国矿业大学学报,2006,35(4):549-555.
LI Yong,SHAO Cheng.Application research of grey soft sensor for charge ratio of media[J].Journal of China University of Mining&Technology,2006,35(4):549-555.
[7]李 勇,邵 诚.一种新的灰关联分析算法在软测量中的应用[J].自动化学报,2006,32(2):311-317.
LI Yong,SHAO Cheng.Application of a novel grey relation analysis algorithm to soft sensor[J].Acta Automatica Sinica,2006,32(2):311-317.
[8]王泽红,陈炳辰.球磨机内部参数的三因素检测[J].金属矿山,2002(1):32-34.
WANG Zehong,CHEN Bingchen.Tri-factor testing of the internal parameters of ball mill[J].Metal Mine,2002(1):32-34.
[9]汤 健,赵立杰,岳 恒,等.磨机负荷检测方法研究综述[J].控制工程,2010,17(5):565-570.
TANG Jian,ZHAO Lijie,YUE Heng,et al.Present status and future developments of detection method for mill load[J].Control Engineering of China,2010,17(5):565-570.
[10] 沈志远,王黎明,陈方林.基于有限长序列分析的Welch法谱估计研究[J].计算机仿真,2010,27(12):391-395.
SHEN Zhiyuan,WANG Liming,CHEN Fanglin.Research on spectral estimation using welch method based on analysis of finitelength sequence[J].Computer Simulation,2010,27(12):391-395.
[11] 李海波,柴天佑,岳 恒.浮选工艺指标KPCA-ELM软测量模型及应用[J].化工学报,2012,63(9):2892-2898.
LI Haibo,CHAI Tianyou,YUE Heng.Soft sensor of technical indices based on KPCA-ELM and application for flotation process[J].CIESC Journal,2012,63(9):2892-2898.
[12]奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用,2011,47(3):123-128.
FENG Guohe.Parameter optimizing for support vector machines[J].Computer Engineering and Applications,2011,47(3):123-128.
[13] 余 晖,赵 晖.支持向量机多类分类算法新研究[J].计算机工程与应用,2008,44(7):185-189.
YU Hui,ZHAO Hui.New research on multi-classification based on supportvectormachines[J].ComputerEngineeringandApplications,2008,44(7):185-189.
[14] 崔晓祥,李 娟.基于支持向量机回归的电力系统负荷建模[J].江苏电机工程,2010,27(12):391-395.
CUI Xiaoxiang,LI Juan.Load modeling based on SVM in power system[J].Jiangsu Electrical Engineering,2010,27(12):391-395.
[15] 梁朝霞.球磨机负荷检测软测量建模方法的研究[D].沈阳:东北大学,2008.
LIANG Chaoxia.Research on soft-sensing method of ball mill Load[D].Shenyang:Northeastern University,2008.
