基于在线层次化非负矩阵分解的文本流主题检测

涂 鼎, 陈 岭, 陈根才, 吴 勇, 王敬昌

(1.浙江大学 计算机科学与技术学院,浙江 杭州 310027； 2.浙江鸿程计算机系统有限公司,浙江 杭州 310009)



基于在线层次化非负矩阵分解的文本流主题检测

涂 鼎1, 陈 岭1, 陈根才1, 吴 勇2, 王敬昌2

(1.浙江大学 计算机科学与技术学院,浙江 杭州 310027； 2.浙江鸿程计算机系统有限公司,浙江 杭州 310009)

针对文本流主题检测中存在的主题结构扁平问题,提出在线的层次化非负矩阵分解方法,在每个时间片中根据归一化累计折损增益选择主题节点进行分解,接着反复将文档分配给最相关的主题节点构建主题层次,该过程中假设主题在由不同时间片中相似主题节点构成的序列中连续再演化,在当前时间片对主题节点进行分解时考虑过去时间片中主题节点的分解结果.该方法不仅能在线的发现和更新文本流中的主题,而且还可揭示主题间的结构关系.在Nist TDT2数据集上的实验结果表明,该方法在NMI、Micro F1、MAP和NDCG等指标下均显著超过了其他动态NMF方法,并在时间效率上显示出一定优势.

动态主题模型；层次聚类；非负矩阵分解

在持续的文本流中去检测潜在的主题是典型的主题发现和跟踪场景(topic detecting and tracking, TDT)[1-6].自动从大量文档流中去发现其中一些有意义的主题模式或者跟踪其中主题内容的变化在许多应用领域具有重要意义,如社交网络、新闻热点分析等.

近年来,对于文本主题的发现和跟踪受到国内外研究者的广泛关注.其中比较重要的一类方法是基于主题模型的方法[7-9],这类方法通常将主题描述为在词表上的一个多项式分布,而文档则是这些主题的一个混合.传统主题模型通常是静态模型,因而无法满足在流式数据中挖掘主题的需要.针对该问题,学术界提出了各种动态主题模型,旨在准确捕捉文本流内容的动态演化特征.根据建模方法的不同,现有动态主题模型方法主要可分为2类：第1类方法基于概率模型去发现文本流中的主题[1-3].第2类方法则是基于字典学习(dictionary learning)或者非负矩阵分解(nonnegative matrix factorization, NMF)[4-6].与基于概率模型的方法相比,基于矩阵分解的方法通常消耗更少的时间.

现有大多数基于NMF的动态主题模型方法将各个潜在主题视为独立的元素,忽略了各个主题的交集和其间的关系,因而限制了这些模型的表达能力.层次结构是克服这一缺陷的可行方案[10-14].然而,现有层次主题模型[10-14]中大部分方法都是静态模型,无法满足检测文本流中主题的要求.目前,仅有Hu等[14]对在线层次主题模型进行探索,但该文中生成的主题层次不满足传统主题层次中子节点是父节点的子集这一假设.

针对上述问题,本文提出了一种在线层次NMF框架(online hierarchical NMF,OHNMF).OHNMF在每个时间片中根据归一化累计折损增益选择主题节点进行分解,接着反复将文档分配给最相关的主题节点来构建主题层次,该过程中对主题节点进行分解时考虑过去时间片中主题节点的分解结果,实现主题在由不同时间片中相似主题节点构成的序列中的连续演化.该层次化划分方法不仅能对文档流中潜在主题的变化进行在线跟踪,也能发现各个主题之间的结构关系的变化.

1 基于OHNMF的在线主题检测

假设某个时间片t内输入的m×n维文档矩阵为Xt,其中m为整个词表的维度,n为整个矩阵中文档的数量.基于矩阵分解的主题模型中的一个常见假设是一个潜在主题可以看作是在词表上的分布,即一个主题就是在Rm空间里的一个列向量w.通过将k个主题向量水平组合起来可以得到一个m×k维的主题-词矩阵Wt,k为主题数目.每一列代表一个主题.除主题-词矩阵之外,模型中另一个矩阵就是主题-文档矩阵Ht.Ht中的每一列表示一个文档在所有主题上的分布.在基于矩阵分解的主题模型方法中,通常使用WtHt去近似文档矩阵Xt.由于在Wt和Ht中出现负数将无法解释各项分布的物理含义,在求解Wt和Ht时需要加上非负约束.这样,一个主题检测问题就可以转化为一个非负矩阵分解问题：给定一个主题数目k和一个时间片内的m×n维文档矩阵Xt,目标是找到一个m×k维主题词矩阵Wt和一个k×n主题-文档矩阵Ht,满足以下条件:

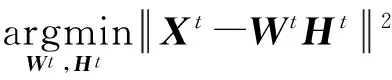
(1)

1.1 在线稀疏NMF

本文所提方法是基于在线稀疏非负矩阵分解(online sparse NMF,ONMF),由在线稀疏字典学习(online sparse dictionary learning)[4]加上非负约束后扩展而成.稀疏NMF与基本NMF的区别在于稀疏NMF在目标函数中引入了稀疏性约束.引入稀疏性约束可增强分解结果的可分离性.通常稀疏性约束是加在主题-文档矩阵Ht,即保证每篇文档在各个主题上的分布只集中在少数主题上.加入稀疏约束后,原目标函数变为

(2)

这里是将Ht的L1范数作为稀疏约束加入到目标函数中,λ为稀疏约束的权重系数.通过引入稀疏性约束,目标函数可以保证从所有可能分解结果中找到高质量的具有较少重合的那些潜在主题.层次化划分方法通常假设同一父节点的子节点的数据是完全分离的或者具有较少重合.通过引入稀疏性约束,NMF的结果可以更好地满足构建主题层次的需求.

动态主题模型的特点是可根据当前新到的数据Xt对原有主题Wt-1进行调整,使得当前主题Wt既能满足历史数据X0-Xt-1的分布,也能适应现有数据Xt的情况,即满足如下目标函数：

(3)

式中:j为t之前的任意时间片,这里Hj为第j个时间片的主题-文档矩阵,Xj为第j个时间片的文档矩阵.该目标函数在求解Wt时既考虑了对当前时间片文档集的拟合,也考虑了对以前所有时间片文档集的拟合,保证了主题-词矩阵Wt-1和Wt的平滑过渡.σ(t,j)为时间尺度函数,其根据t和j之间的时间间隔来调整j时间片数据在当前分解过程中的权重.通常其是一个指数函数,如σ(t,j)=αt-jα≤1.过去越久的数据会获得更小的权重.

式(3)中的目标函数可用更新算法1来求解.在第3步,使用LARS-Lasso得到当前最优的hi.第4步中根据xi和hi更新辅助矩阵A和B.A和B矩阵是分解辅助矩阵,可看作用于存储过去分解过程的中间结果,即与xi和hi相关历史信息.β为时间尺度系数,替代σ(t,j).其意义为每新到一个文档,之前所有文档的权重变为原来的β倍,β的取值范围为0～1.第5-12步根据A和B更新W每一列直到收敛为止.算法收敛性分析可见[4].如果没有之前分解结果,可随机初始化W,并将A和B初始化成全为0的矩阵.通过算法1中的优化更新规则,可动态得到最新的W,然后通过LARS-Lasso计算得到当前时间片的H.

算法1 在线更新主题-词矩阵

输入: 文档矩阵Xt=[x1, x2, x3,…, xn],上一次分解结果中的m×k维主题-词矩阵Wt-1,L1正则化约束的系数λ,分解辅助矩阵A∈Rkxk,B∈Rmxk

1. W←Wt-1

2. For xi∈Xt

3. 使用LARS-Lasso [4]找到满足条件的hi

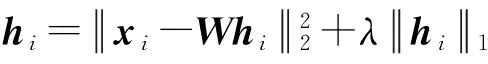
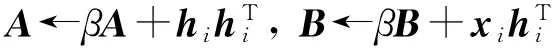
5. W=[w1, w2, w3,…, wk] A=[a1, a2, a3,…, ak]

B=[b1, b2, b3,…, bk],target=1

6. While target没有收敛

7. Forj=1 tok

8. wj=(bj-Waj)/A[j,j]+wj

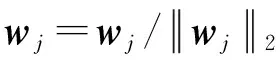
10. End For

11. target=Tr(WTWA)/2-Tr(WTB)

12. End While

13. End For

输出：当前时间片的主题-词矩阵W

1.2 OHNMF整体流程

图1 OHNMF整体流程Fig.1 Overall process of OHNMF

基于ONMF的OHNMF方法的整体流程如图1所示.在时间片t=1,系统执行一个基本的层次化NMF方法并且生成一个主题层次.在层次化NMF的过程中,系统首先将该时间片内的所有文档X放到根主题节点中并进行一次矩阵分解.将生成的主题-词矩阵Wr的每一列作为该根主题节点子节点的主题向量,并且根据Hr将文档分配到各个子主题节点中.对于文档xi,存在对应的文档-主题向量hi∈Hr,hi中最大值所对应的主题节点即xi被分配到的节点.然后找到可分性(2.3节)最高的叶节点进行同样的分解过程,该过程反复迭代直到满足特定终止条件：1)叶节点的数量达到预先定义的主题数目k,该条件一般用以防止层次化过程迭代过多；2)所有叶节点均不可分,即该节点中所有文档都集中于某一个主题.

所有文档将沿着主题层次中的路径划分到各个叶主题节点中.主题层次中的每个主题节点都可以表达为一个主题向量w,并且包含一个集合D记录所有划分路径经过该主题节点的文档.在生成主题层次的同时,系统还为每个主题节点存储了辅助矩阵来记录该主题节点的历史分解信息,即算法1中的辅助矩阵A和B.

在下一个时间片,参考上一时间片分解的历史信息生成一个新的主题层次,该阶段OHNMF算法伪代码如算法2所示.在根主题节点处,所有当前时间片的文档矩阵Xt将结合上个时间片根节点的Wt-1,At-1,和Bt-1进行分解(1～4步).对于非根节点w的分解过程(9～13步),其首先找到在上一个时间片最相关的主题节点wr(10步).然后结合wr过去分解的信息对w进行在线分解(11步).例如,在图1中,w2在分解时考虑了在上个时间片与其最相似的w1的分解信息.相似的关系也存在于w3和w2之间.整个流程可以看作主题w1在一个由D1、D2和D3组成的文本流中经过w2演化成w3.这样,本文方法可以追踪主题的演化过程.对于那些在过去时间片未能找到相关主题的主题节点,将被视为新出现的主题并进行独立的分解.

算法2 在线更新主题层次

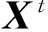
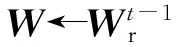
3. W=ONMF (Xt,λ,A,B); 并将W存储在数组lw,将W和当前的辅助矩阵保存到SW′和辅助矩阵的集合 SA′, SB′中

4. 计算W子节点的mNDCG乘积并存储在数组lm

5.n=n+1;

6. Whilen0

7. 找到下一个待分解主题节点w,其子节点mNDCG乘积最大.并从lw中取得其主题-词矩阵W和所属文档矩阵X

9. For wi∈w1, w2

10. 生成当前节点摘要si,找到在上一个时间片拥有最相似摘要sj的主题节点wj

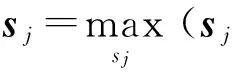
11. 重复2～4步.如果没有找到相似节点,则视其为一个全新节点的分解.

12. EndFor

13.n=n+1;

14. End While

输出:t时间片的所有节点的主题-词矩阵的集合SW′和辅助矩阵的集合 SA′, SB′

1.3 OHNMF细节

每个节点处的主题-文档矩阵W的维度被设置为m×2,即每个主题节点包含2个子主题节点,这样设置有以下几点好处：1)在二叉树中将数据划分给某个子节点会比比较容易.2)整个计算过程将会被加速.通常NMF的优化求解时间至少与潜在主题数目k成线性相关.通过分析可以得到在这种设定下,每个主题节点的分解过程将被加快.假设一个新文档的在ONMF的分解过程中消耗k个时间单位,那么在有k个叶节点的OHNMF中其过程将消耗2(log2k+1)个时间单位.如果最终整个叶节点的数目较大,那么节省的时间比例是相当可观的,即(k-2 log2k-2)/k.

在每一次迭代过程中,OHNMF选择可分性最高的叶节点作为下一个分解的节点.这里使用经过修改的归一化累计折损增益[10](modified normalized discounted cumulative gain,mNDCG)作为衡量节点可分性的标准.NDCG可以比较一个系统生成的排序与目标排序之间的一致性.根据每个主题向量中各个词的权重可以生成主题中词的一个排序,这样可以通过比较父主题节点和子主题节点中词的排序来得到其间的一致性.假设父节点的排序为

fP=f1,f2,f3, …,fm,2个子节点的排序为fL=fl1,fl2,fl3, …,flm,fR=fr1,fr2,fr3, …,frm那么其mNDCG可计算为

g(fi)=

log (m-i+1)/log (m-max (i1,i2)+1).

(4)

(5)

mNDCG(fS)=mDCG(fS)/mIDCG.

(6)

式中：mDCG为改进的累计折损增益(modified discounted culmulative gain), mIDCG为改进的理想累计折损增益(modified idea discounted culmulative)i1,i2即父节点中排序在第i个位置的词在2个子节点中的排序.fS可以是fL或fR.mIDCG即父节点的mDCG值.mNDCG除考虑了父节点与子节点的相似度之外,还引入了2个子节点之间的差异性.算法在每生成一个新的主题节点时,都会对其进行一次预分解以获得其mNDCG值,并将2个子节点mNDCG的积作为评价分数,越大的可分性越高.2个子节点之间差异越大且都与父节点相似的那些父节点将获得更高的分数.如果该节点中所有文档几乎都分到同一个子节点中,其分数将被设为-1,即新节点主要由一个主题的文档构成且不需要进一步分解.

为了跟踪主题的演化过程,在2个时间片t和t-1中具有高相关性的主题wi、wj被视为在2个不同时间片里的同一个主题.如果wi、wj的相似度大于特定阈值,那么t时间片里的主题节点wi可能由t-1时间片的主题节点wj演化而来.为了描述连续时间片中2个不同主题节点wi、wj的相似度,首先需要得到这些主题节点的摘要以减少平凡词的影响.一个主题的摘要s由与该主题最相关的nr个词的词频信息所构成.词与主题节点w的相关程度由该词在该主题节点所有文档的TF-IDF值决定.这样主题节点的摘要即TF-IDF最高的前nr个词词频的平均值.其他词的词频被设置为0.给定2个主题节点的摘要si,sj,其之间的相关程度可以由余弦值得到

(7)

如果t-1时间片中存在与当前主题节点wi相似度大于一定阈值的主题点节点,即可认为当前主题节点是由t-1时间片中与当前节点相似度最大的主题节点wj演化而来,可利用其分解结果指导当前节点wi的分解过程.

基于NMF的方法中,矩阵初始化一直是影响分解结果的关键因素.由于ONMF在初始几次迭代中将以较大的步幅更新W,其对于初始的几个文档数据分布比较敏感,可以通过恰当的初始化解决这种问题.在分解一个节点的数据X时,如果没有找到之前相似的节点,则首先对其进行kmeans聚类来得到2个类,然后将这2个类的中心作为初始的主题-词矩阵W0,同时设置A0=t0I,B0=t0W0,t0是常量,这里可以看作当前分解是在另一次分解之后进行的,该次分解得到的主题-词矩阵是W0,且记录的分解辅助矩阵是A0和B0.因为A0和B0决定了更新时的步幅,这样设置避免了ONMF对于初始数据敏感的问题.

2 实验与分析

在实验部分本文方法将与其他现行方法进行比较,并且采用多种标准来衡量实验结果以验证本文方法的有效性.所有实验均运行在MATLAB R2014a 环境中,运行机器配置为Intel Pentinum G3220处理器和24G内存.

2.1 数据集

本文实验是在Nist主题检测和跟踪文档集(nist topic detection and tracking corpus, TDT2)上进行的[15].该文档集中包含1998年上半年从6个数据源中所采集到的11 201个文档,包括2个新闻专线(APW,NYT),2个广播节目(VOA,PRI),和2个电视节目(CNN,ABC).所有文档被划分到96个语义类别中.在本文实验中,所有属于2个及以上类别的文档都被去除并且只保留最大的30个类别,共9 394个文档.去除停用词后词表大小大约为36 000.

对于每一个不同的主题数目k,实验中都会在此设定下生成50个TDT2的采样子集.比如当k=2时,所有方法将会在只包含2类文档的50个采样子集上运行一遍并比较结果.为了满足实验对时序性的要求,所有采样子集中的数据都根据时间进行了重新排序(原始数据是根据类别标签排序).为了提高性能并且加速运行过程,在预处理时对文档进行了降维.对于每一个子集,词表大小被压缩到原来大小的40%,如每一个子集在去除掉频率为0的词之后词表的大小大约为10 000～20 000,按照TF-IDF值对所有词进行排序,取最大的前40%作为最终的词表.所有文档都根据其长度进行了归一化以减少文档大小对实验建模的影响.

2.2 实验评价标准

采用4种标准评价实验中各种方法的效果：

归一化互信息(NMI)：NMI是一个广泛使用的聚类质量评价标准.在生成的聚类数目与真实聚类数目不同时具有一定优势,并且可以用于决定最优的聚类数目.对于数据的2个不同划分而言,越高的互信息值代表着这2种划分之间有更高的相似度,其计算公式为

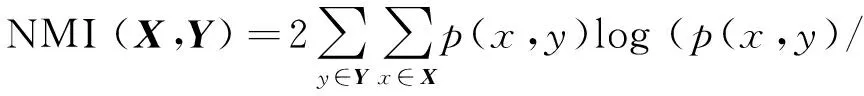
(p(x)p(y)))/(H(X)+H(Y))

(8)

式中:X,Y分别为对数据集的2个不同划分,H(X)为分布X的熵.p(x)、p(y)和p(x,y)分别为x的分布概率、y的分布概率和x、y的联合分布概率.

微平均F1值(Micro averaged F1,MicroF1)：这是另外一个广泛使用的用于衡量聚类质量的评价标准.与归一化互信息相比较,微平均F1在聚类数目较大时能够更准确地衡量聚类方法的性能.假设在聚类结果中一共生成了k个聚类且所有文档的真实标签为1到l,即真实聚类为l个.那么对于每一个真实聚类Ci可以从聚类结果中发现一个结果Cri,满足Cri与Ci的交集所含数据点最多,那么最终的微平均F1可以通过如下公式计算得到

(9)

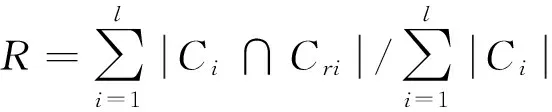
(10)

F1=2PR/(P+R).

(11)

式中：R和P分别为召回率和准确率.召回率和准确率的计算与微平均F1中相同.

中间平均准确率(mean average precision, MAP)：微平均F1值从单点值的角度衡量聚类性能.而中间平均准确率则是从宏观角度去评估聚类方法的性能,计算公式为

(12)

最终所有50个数据子集的实验结果被用于计算中间平均准确率.

归一化累计折损增益(normalized discounted cumulative gain, NDCG)：归一化累计折损增益通常用于衡量发现的主题的质量.对于每一个真实主题都可以生成一个所有属于该主题的文档向量的平均向量.然后从生成的聚类结果中找到一个与真实主题交集最大的聚类,计算真实主题平均向量与属于该聚类的主题向量之间的NDCG值,越大说明发现的主题质量越高.主题中概率最大的前N个词的NDCG为

NDCG=DCG/IDCG

(13)

式中：r(j)为第j个词与真实主题分布的相关性,DCG为累计折损增益(discounted culmulative agin), IDCG为理想累计折损增益(idea discounted culmulative gain), IDCG即可能的最大DCG值.

2.3 实验对比方法

为了能够更好地评估本文所提方法,实验中选取了5种基准方法：

fix-NMF-L1: fix-NMF-L1只在第1个时间片的数据上执行NMF分解并且在后来的时间片中不再改变各个潜在主题向量的分布.该NMF算法的实现是基于L1稀疏约束和乘法更新规则的[16].

t-NMF-L1:t-NMF-L1使用与fix-NMF-L1相同的NMF实现.区别在于t-NMF-L1在时间片t使用Wt-1作为初始化矩阵,即用上一个时间片的主题-词矩阵Wt-1作为t时间片的初始化主题-词矩阵.

Hie-NMF-L1：Kuang等[10]提出的Hie-Rank2方法可以通过反复执行rank2-NMF实现文档的层次化聚类.rank2-NMF是一种基于活动集(active-set)的快速NMF算法,其秩k设为2.为了提高Hie-Rank2算法的效果,rank2-NMF被替换成了NMF-L1.在每一个时间片都会执行一次Hie-NMF-L1.

JPP: JPP[6]是一个基于时间的协同矩阵分解算法,可以发现文本流之中的潜在主题.其在目标函数中考虑了之前时间片的分解结果和当前时间片分解结果之间的差异.通过在目标函数中加入这种约束,其可以实现平滑的主题发现.

ODL: ODL[4]是一个在线字典学习方法.在本实验中其目标函数里加上了非负限制.

实验中每个时间片窗口大小被设为500个文档,本文方法在时间尺度函数上使用的是基于文档数的权重调整,所以在实验中将文档数目固定比较好观察不同时间尺度函数参数的影响.其基本与每个子集中一个月内的文档数量相同.对于所有添加了L1约束的方法,其系数λ均被设为0.01.根据文献[17],λ最好设置为m-1/2,即在本实验中设置为0.01.所有方法的最大迭代次数都被设为1 000.

OHNMF中每一个聚类所能包含的最小文档数设为5.ODL和OHNMF中的时间尺度参数β被设为0.999 5,即第(n-500)文档的分解结果对第n个文档分解的权重约为0.8.摘要词表的大小nr被设为100.主题相关度的阈值被设为0.7,即前后2个时间片如果存在相似度超过0.7的主题节点即可认为这2个节点在时间上是连续变化的.原因是该值要大于0.5且小于1,所以本文选择了一个略小于0.5和1的平均值的值.JPP和Hie-NMF-L1中其他参数的设置均与各自论文中设置相同.余下所有实验的参数设置如无特别说明均与以上参数设置相同.所有方法均使用kmeans方法得到初始的主题-词矩阵.

2.4 主题质量

本实验中对比了不同k(k=5、10、15)设定下各种方法发现主题的质量.实验数据的详细信息如表1所示.实验中所对比的6种方法的结果如表2所示.

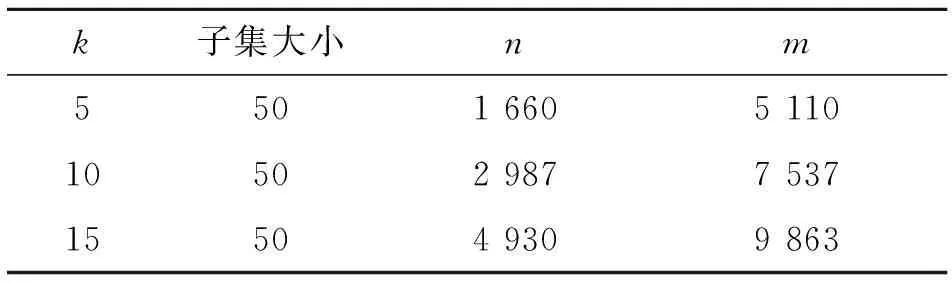
表1 抽样后的Nist TDT2数据统计信息

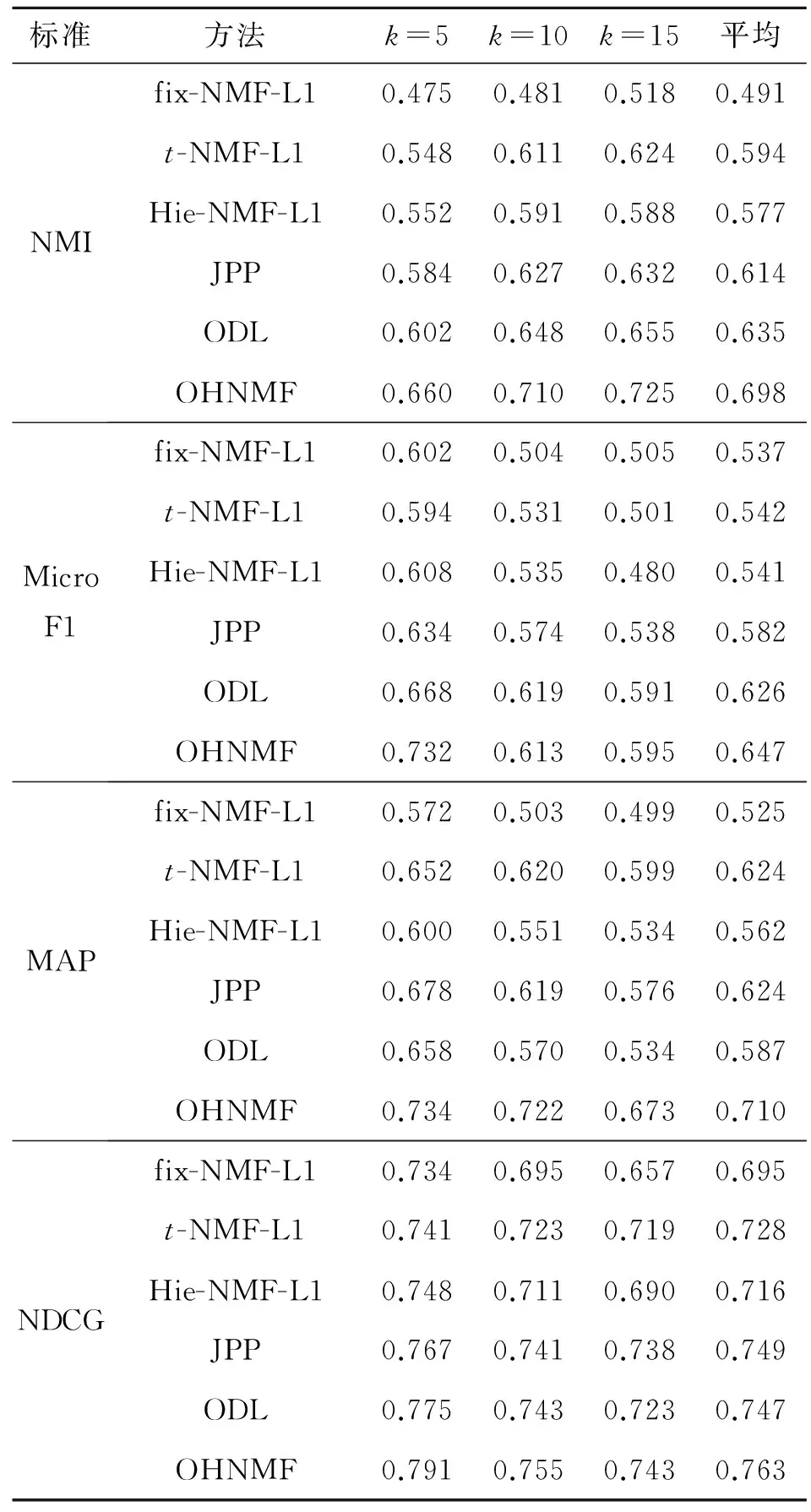
表2 各主题检测方法在Nist TDT2上的主题质量对比

从表2可以看出：fix-NMF-L1在6个方法中表现最差,原因很简单：在不同时间片之间主题-词的分布和主题-文档的分布是不断变化的,用固定的模型去检测构成文档的潜在主题自然不会取得较好的效果.在某种程度上t-NMF-L1可以看作是一个在线分解模型,因为相邻2个时间片的主题-词矩阵之间存在一些“一致性”(从下一个实验中可以看到这一点).但是这种相邻2个主题-词矩阵之间的“一致性”并没有像其他在线方法那样严格的定义到目标函数中,所以其效果不如其他3个在线分解方法.

3个在线分解方法：JPP,ODL和OHNMF在本实验中表现出了较好的性能.JPP方法获得了较高的MAP值,而ODL获得了较高的微平均F1值.在所有对比方法中,本文所提方法获得了最好的效果,原因是本文方法在层次划分过程中将属于不同主题的文档的主要部分较好地分隔开了,减少了他们之间在在线分解时可能存在的影响,从而提高了所获得的主题的精度.由于这样所获得的结果比较稳定,所以不会出现ODL或者JPP这样只在某项指标上会表现比较好的情况.

在层次化NMF类的方法的对比中,OHNMF要优于Hie-NMF-L1.原因是OHNMF可以用过去时间片的分解结果来指导当前时间片的分解过程,可以获得全局更优的分解结果.而Hie-NMF-L1只能根据当前时间片的文档来进行分解过程.实验中同样评估了Hie-NMF-L1的原始形式Hie-Rank2.在本文实验场景中Hie-Rank2没有取得很好的效果,相比于Hie-NMF-L1,其各项指标的分数下降0.1.对于OHNMF而言,如果不添加L1稀疏性约束,其在某些指标上同样会出现0.05的下降.原因是层次化过程中将会放大划分时的错误.所以在每个主题节点的分解过程应该越准确越好.通过加入L1正则化约束,OHNMF可以找到更稀疏的主题表达,这样属于不同主题的文档就能够被更好的划分开.

实验中同样可以观察到NMI的值基本上随着k的增大而增大(MicroF1和MAP在随着k的增大而减小),部分说明在聚类数据较大时NMI不能较好的衡量聚类效果.

2.5 主题平滑度

本实验中评估了相邻2个时间片中主题-词矩阵之间的平滑度.Wt-1和Wt之间的平滑度可以通过如下方法计算：

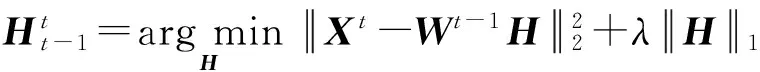
(14)

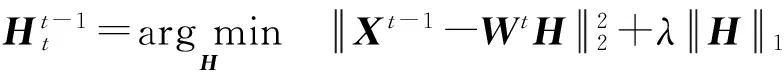
(15)

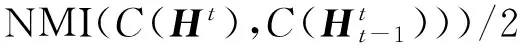
(16)

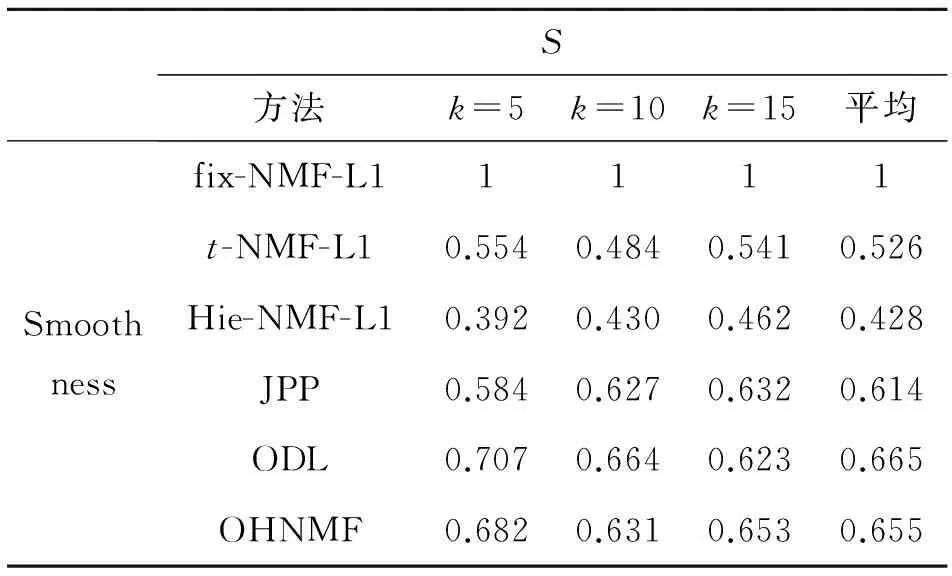
表3 各主题检测方法在Nist TDT2上的主题平滑度对比

因为在主题检测的过程中主题-词矩阵一直没有发生变化,所以fix-NMF-L1方法的主题平滑度是1.排除在线学习因素的影响,扁平分解方法相对于层次分解方法能获得更高的主题平滑度.原因可能是对于一些处于主题聚类边界上的文档,扁平分解能够获得较高的一致性,而层次分解可能根据当前数据对其有一定的调整.t-NMF-L1表现的比Hie-NMF-L1好的另外一个原因是t-NMF-L1是一种半在线的方法,其每次使用上一个时间片的主题-词矩阵作为当前分解的初始化矩阵.OHNMF获得了第2高的主题平滑度,时间参数β和主题相关度的阈值将会影响到主题平滑度.额外实验表明本文方法设置更大的β和更小的阈值都可获得更加平滑的主题.

2.6 运行时间

本实验对比了各个方法的运行时间.所有方法的默认数据设置是文档数n=2 000,主题数k=10,词表大小m=4 000.运行时间为10次运行的平均时间.所有方法中的窗口大小均设置为与文档数目n相同.各个方法在不同m、k和m设置下的运行时间t如图2～4所示.

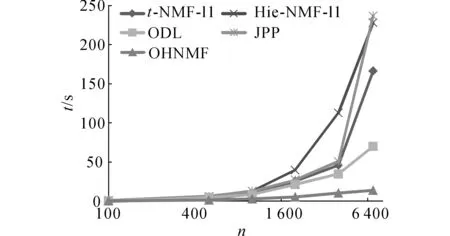
图2 各方法在不同文档数目下的运行时间Fig.2 Computation time of all methods under different document numbers

图3 各方法在不同主题数目下的运行时间Fig.3 Computation time of all methods under different topic numbers

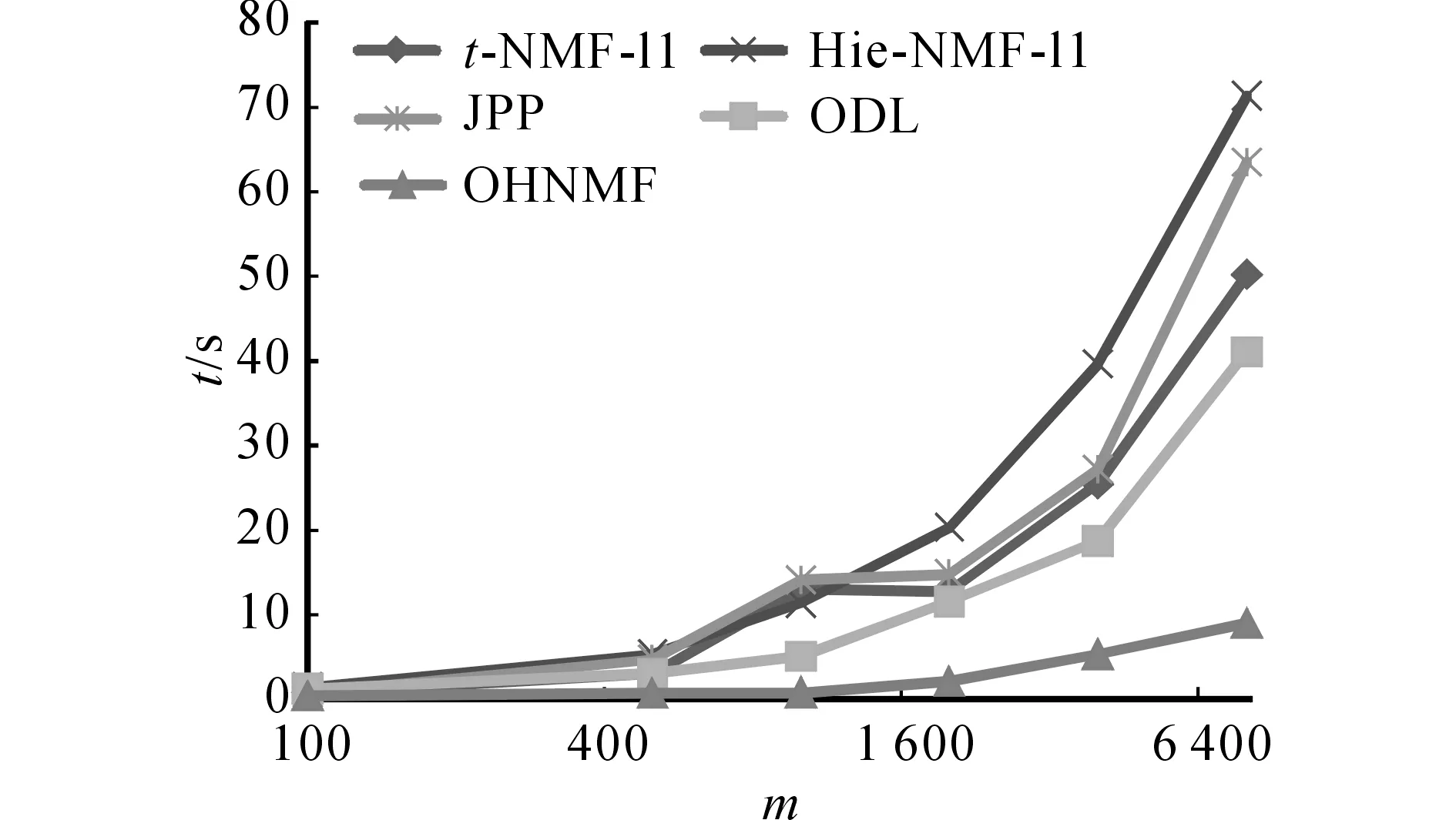
图4 各方法在不同词表大小下的运行时间Fig.4 Computation time of all methods under different vocabulary sizes

从实验结果中可以看出ODL和OHNMF花费了最少的运行时间.从图2中可以看出,随着文档数n的增长运行时间的变化,Hie-NMF-L1和JPP的时间增长的最快,OHNMF与ODL增长最慢.从图3中可以看出,随着主题数k的增长运行时间的变化,t-NMF-L1增长的最快,OHNMF最慢,其他3种方法趋势差不多,这与本文前面分析相符.从图4中可以看出,随着数据维度m的增长运行时间的变化,Hie-NMF-L1和JPP的时间增长的最快,OHNMF增长的最慢.综上所述,OHNMF在时间效率上是所有对比方法中最优的,在数据规模增长时的可扩展性是最强的.

3 结 语

对文本流中的潜在主题进行检测和跟踪是当前数据挖掘领域的一个热点.本文提出了一种层次化的在线稀疏非负矩阵分解方法且将本文方法与其他当前方法在Nist TDT2数据集上进行比较,实验证明本文提出的方法在更短的运行时间内取得了更好的结果.未来后续工作主要有以下几个方向,1)目前方法对于周期性出现的话题没有较好地拟合2)本文方法能够捕捉到发现的主题之间的结构关系,可进一步根据这些结构关系去生成更加可理解的主题层次.

[1] BLEI D M, JOHN D L. Dynamic topic models [C]∥Proceedings of the 23rd International Conference on Machine Learning. Pittsburgh, Pennsylvania: ACM, 2006: 113-120.

[2] WANG C, BLEI D M, HECKERMAN D. Continuous time dynamic topic models [C]∥Uncertainty in Artificial Intelligence. Helsinki, Finland: AUAI Press, 2008:579-586.

[3] WANG X, ANDREW M. Topics over time: a non-markov continuous-time model of topical trends [C]∥Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Philadelphia, PA： ACM, 2006: 424-433.

[4] MAIRAL J, FRANCIS B, JEAN P, et al. Online learning for matrix factorization and sparse coding [J]. Journal of Machine Learning Research. 2010, 11: 19-60.

[5] SAHA A, VIKAS S. Learning evolving and emerging topics in social media: a dynamic nmf approach with temporal regularization [C]∥Proceedings of the Fifth ACM International Conference on Web Search and Data mining. Seattle, Washington: ACM, 2012: 693-702.

[6] VACA C K, AMIN M, ALEJANDRO J, MARCO S. A Time-based collective factorization for topic discovery and monitoring in news [C]∥Proceedings of the 23rd International Conference on World Wide Web. Seoul： ACM, 2014: 527-538.

[7] BLEI D M, NG A Y, JORDAN M I. Latent dirichlet allocation [J]. Journal of Machine Learning Research, 2003, 3: 993-1022.

[8] THOMAS H. Probabilistic latent semantic analysis [C]∥Uncertainty in artificial intelligence. Stockholm, Sweden: Morgan Kaufmann, 1999: 289--296.

[9] GAUSSIER E, GOUTTE C. Relation between PLSA and NMF and implications [C]∥Acm Sigir Conference on Research & Development in Information Retrieval. Salvador, Bahia, Brazil: ACM, 2005: 601-602.

[10] KUANG D, HAESUN P. Fast rank-2 nonnegative matrix factorization for hierarchical document clustering [C]∥Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. Chicago, Illinois： ACM,2013: 739-747.

[11] JENATTON R, MAIRAL J, OBOZINSKI G, et al.. Proximal methods for sparse hierarchical dictionary learning [C]∥International Conference on Machine Learning. Haifa, Israel: Omnipress, 2010: 487-494.

[12] 景丽萍,朱岩,于剑.层次非负矩阵分解及在文本聚类中的应用[J].计算机科学与探索,2011, 5(10): 904-913.

JING Li-ping, ZHU Yan, YU jian. Hierarchical non-negative matrix factorization for text clustering [J]. Journal of Frontiers of Computer Science & Technology, 2011, 5(10): 904-913.

[13] BLEI D M, GRIFFITHS T L, JORDAN M I, et al. Hierarchical topic models and the nested chinese restaurant process [C]∥Proceedings of the 17th Annual Conference on Neural Information Processing Systems. Vancouver, British Columbia, Canada: MIT Press, 2003: 17-24.

[14] HU L, LI J-Z, ZHANG J, et al. o-HETM: an online hierarchical entity topic model for news streams [C]∥ Proceedings of the 19th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Ho Chi Minh City, Vietnam: Springer, 2015: 696-707.

[15] CAI D, MEI Q, HAN J, et al. Modeling hidden topics on document manifold [C]∥Proceedings of the 17th ACM conference on Information and knowledge management. Napa Valley, California: ACM, 2008: 911-920.

[16] CICHOCKI A, ZDUNEK R, PHAN A H, et al. Nonnegative matrix and tensor factorizations: applications to exploratory multi-way data analysis and blind source separation [M]. Hoboken, New Jersey. John Wiley & Sons, 2009: 131-139.

[17] RITOV Y, BICKEL P J, TSYBAKOV A B. Simultaneous analysis of lasso and dantzig selector [J]. Annals of Statistics, 2009, 37(4):1705-1732.

Hierarchical online NMF for detecting and tracking topics

TU Ding1, CHEN Ling1, CHEN Gen-cai1, WU Yong2, WANG Jing-chang2

(1.CollegeofComputerScienceandTechnology,ZhejiangUniversity,Hangzhou310027,China;2.ZhejiangHongchengComputerSystemsCompanyLimited,Hangzhou310009,China)

An online hierarchical non-negative matrix fraction method was proposed to address the problem of flat topic structure of text stream topic detecting methods. At every time slot, the topic nodes were oplited-splited according to the normalized discounted cumulative gain and a topic hierarchy was built by iteratively assigning documents to the most related topic nodes. The hierarchy construction process refers the previous topic hierarchy. The underlying assumption is that the topics are evolving among the similar topic nodes in different time slots. The method can detect and track topics in stream in an online way, which reveals many useful relationships between the topics. Experiments on Nist TDT2 dataset show that our method outperforms the contrasting methods under different metrics, e.g. NMI, Micro F1, MAP and NDCG, and uses less execution time.

dynamic topic modeling; hierarchical clustering; nonnegative matrix factorization

2015-07-12.

国家自然科学基金资助项目(60703040，61332017)；浙江省科技计划资助项目(2011C13042，2015C33002);“核高基”国家科技重大专项资助项目(2010ZX01042-002-003)；中国工程科技知识中心资助项目(CKCEST-2014-1-5).

涂鼎，(1987—)，男，博士，从事非结构化数据管理、数据挖掘等研究.ORCID: 0000-0001-8579-2737. E-mail：tututu111@yeah.net

陈岭，男，副教授.ORCID: 0000-0003-1934-5992. E-mail：lingchen@cs.zju.edu.cn

10.3785/j.issn.1008-973X.2016.08.026

TP 311

A

1008-973X(2016)08-1618-09

浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng