物流业对城镇化发展影响研究

张晓华

内容摘要：城镇化的发展在当前经济发展的转型期有着重要的作用，而物流业是带动城镇均衡、持续、稳定、跨越发展的战略性产业。本文采用因子分析法降维、非参数回归等方法来处理物流业对城镇化的影响并进行分析。结果表明，从时间数据上来看，物流业对城镇化的影响是非线性的正向关系，从截面数据上来看，2014年不同区域两者之间正向关系有待考究。

关键词：降维   样条基   自然样条   非参数回归

引言

当前我国已进入经济高速发展的转型期，城镇化发展无疑成为深入发展的重点，其在现代化、经济持续发展、产业结构转型升级、解决农村农民问题、推动区域协调发展、促进社会全面进步等方面有重大的意义。物流业在城镇化发展中具有促进产业分工、吸引产业集聚、提升生活质量、扩大就业数量、带动城镇均衡、持续、跨越、稳定发展的重要作用，是支撑和引导城镇化发展的战略性产业。对于两者之间的关系，国内外研究颇多，研究成果各有建树。然而这些学者大多基于时间序列做定量研究，且采用降维后再引入样条非参数回归的方法更是鲜有人涉及。因此，本文采用另一种方法，从一个新的角度阐释物流业对城镇化的影响。

指标设计和模型设定

衡量物流业发展的指标迄今为止没有一个唯一的标准，不同学者所定义的指标也不完全一样。本文根据我国物流发展的实际情况，依据数据的可得性，建立三个一级指标和九个二级指标。一级指标分为经济指标，基础实施和物流规模。经济指标下面的二级指标分为地区产总值，地区交通运输、仓储和邮政业增加值和地区社会消费品零售总额。基础设施下面的二级指标分为地区公路里程。物流规模下面的二级指标分为地区邮电业务总量、地区货运量、地区货物周转量、地区客运量和地区旅客周转量。采用因子分析法将衡量物流业发展的九个指标降维成一个指标x。y代表城镇化发展采用城镇化率，最后用非参数回归法来研究物流业x对城镇化y发展的影响。

（一）因子分析法降维

第一步，将所有衡量物流业的变量进行无量纲处理。

第二步，计算相关矩阵的特征根λ和特征向量γ、方差贡献率，根据累计方差贡献率大于85%确定公因子个数。

第三步，用最大化正交法求载荷矩阵（），确定公因子名称和公因子得分。

第四步，用方差贡献率作为权重，和公因子做加权平均得到一个综合得分x。

（二）非参数回归

线性模型虽然简单，解释性强，推断理论也相对成熟，但变量之间若存在着大量的非线性关系，如果仍然用线性关系来研究非线性变量关系，实证结果就会难以让人信服，因此本文选用非参数回归。

为了研究相应变量y和协变量x之间的非线性关系，如模型（1）所示，f（xi）是基函数（可以选用不同的基，本文主要使用多项式基和样条基）。

yi=β0+f（xi）+εi            （1）

若基函数f（xi）是多项式函数，即x1，x2，x3，…，xd的线性组合，这种回归就是多项式回归，d一般不大于3或者4（d越大，多项式曲线就会越光滑，甚至会在x变量定义域的边界处呈现异样的形状）。多项式回归系数的求法可用最小二乘求解。

更加稳定的基函数f（xi）是样条函数，一个有k个结点的三次样条函数可以由b1（x1）、b2（x2）、b3（x3）、…、bk+3（xi）的线性组合构成，其中，bi（xi）有多种选法，本文选用三次多项式为基础，然后在每个结点添加一个截断幂基，即：

yi=β0+β1xi+β2xi2+β3xi3+β4h（xi，ξ1）+……+βk+3h（xi，ξk）+εi     （2）

其中，h（x，ξ）=（x-ξ）3，（x>ξ），h（x，ξ）=0，（x<ξ）。ξ是结点，截断幂基项只会使三次多项式在ξ处的三阶导数不连续，而在每个结点，函数本身、一阶导数、二阶导数都是连续的。在边界的结点外，函数是三次多项式，估计模型时，仍然采用最小二乘法估计k+4个系数。

虽然三次样条函数相对稳定，然而在预测变量之外的区域，即x取较大值或较小值时，有较大方差，体现在图形中是边界区域置信带较宽，自然样条，即模型（3）弥补了这点。

yi=β0+β1xi+β4h（xi，ξ1）+……+βk+3h（xi，ξk）+εi                        （3）

其中，h（x，ξ）=（x-ξ）3，（x>ξ），h（x，ξ）=0，（x<ξ）。三次自然样条函数可以看作是三次样条并附加了边界约束（二阶和三阶导数为0）的回归样条，在边界的结点外，函数为一次多项式，估计模型时，依然采用最小二乘法估计k+2个系数。

物流业对城镇化发展的实证结果与分析

本部分从时间序列数据和横截面序列数据两个角度来研究物流业对城镇化的影响。

（一）时间序列角度

本文通过2015年《中国统计年鉴》收集了2000-2014年每年物流业发展的八个指标的数据，根据因子分析法降维的思想得到了一个主成分（第一主成分达到86.5%）x来衡量物流业的发展。再收集2000-2014年城镇化率的指标数据y来代表城镇化的发展。如表1所示。

表1显示，2000年以来，我国城镇化率快速发展，物流业发展水平也在逐年增加。用R软件对上述城镇化率y和物流业发展x标准化处理后做多项式回归和样条回归拟合，显然非线性拟合比线性拟合更加贴合散点图，如图1所示。从模型的残差标准误上来看，一元一次线性回归是0.1561，4次多项式回归是0.1109，三次样条回归是0.107（结点分别在25%、50%、75%处），自然3次样条是0.135，可见3次样条的模拟结果最好，自然样条在边界处置信带较窄的优势在此并不明显，反而标准误大于三次样条。结果表明，物流业对城镇化影响确是正向关系，即随着物流业发展的增加，城镇化发展也随之加快，两者协调一致。从模拟曲线的斜率来看，城镇化发展随着物流业发展的速率经历了由快到慢再到快的趋势。

（二）截面序列角度

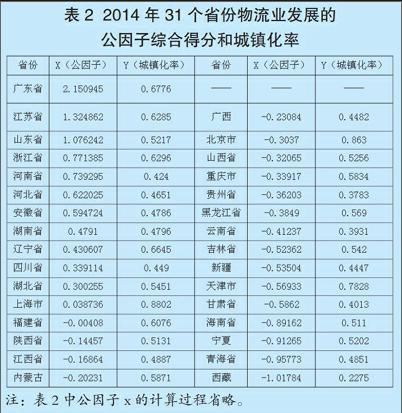
本文通过2015年《中国统计年鉴》收集了2014年我国31个省市自治区（港澳台地区除外）的物流业发展的八个指标的数据，采用同上的方法—因子分析法降维得到两个主成分（累计贡献度达到87.1%），再将其进行加权平均得到最终公因子得分x来衡量物流业的发展。收集2014年31个省市自治区的城镇化率y衡量城镇化的发展，如表2所示。

结果显示，2014年物流业综合发展水平排在前五位的有广东省、江苏省、山东省，浙江省和河南省，这些省份是工业大省和人口大省，其交通运输收益和运力较高，是物资消耗和人员的周转集散地。而排在后五位的省份大多处于西部地区，西部发展较晚，基础设施相对不完善，因此要加大西部地区物流业的发展。

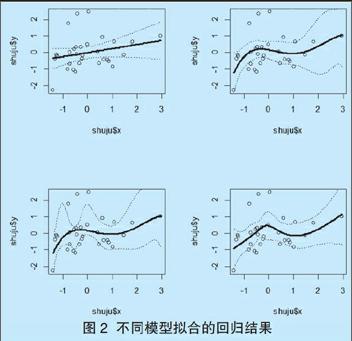
用R软件对上述截面数据城镇化率 和物流业发展 标准化处理后做散点图，显然非线性拟合仍然比线性拟合更加贴合散点图，如图2所示。从模型的残差标准误上来看，一元一次线性回归是0.9858，4次多项式回归是0.9791，3次B样条是0.943，自然3次样条是0.9749，仍然是3次B样条的模拟结果最好。图形显示，物流业对城镇化影响并不像纵向数据那样呈现正向关系，两者之间也并不协调一致，比如河北省、安徽省、湖南省、辽宁省等物流业发展水平相对高的地区（不是最高）其城镇化率却较低，说明2014年全国不同省份物流业对城镇化影响不尽同，高物流水平的省份城镇化率反倒不高，因此物流业对城镇化的因果关系也有待考究。

结论

本文采用非参数回归来研究物流业对城镇化的影响，之所以提出此法是因为非参数回归形式自由，受约束少，且无论从时间序列角度还是从截面序列角度来看，两者之间关系非线性都比线性拟合更好，残差标准误更低。结果发现，我国物流业对城镇化的影响从时间趋势上来看是协调一致发展的，呈非线性正向相关关系，然而从截面角度来看，不同区域物流业对城镇化的影响并不都是正向关系，甚至有负向关系，原因有待进一步考究。此外，非参数回归的方法需要大的样本容量，本文样本量不够大，时间趋势上是15年的数据，截面空间是31个省自治区，所以非参数回归结果有待商榷。

根据实证结果表明，物流业在我国城镇化持续健康发展的过程中具有重要的作用，但全国不同区域地理位置、自然资源、经济发展方式有所差别，具体到各个地区来研究又有很多特点，因此区域物流业对城镇化的影响作用有待考究。因此，应增强城镇化发展的动力，以积极推进物流业带动城镇化高效和谐全面发展。