高维数据降维技术及研究进展
2018-03-08赵逢禹
刘 靖,赵逢禹
(上海理工大学 光电信息与计算机工程学院,上海 200093)
随着多媒体技术和计算机技术的高速发展,大规模的数据维度呈爆炸性增长。伴随着数据维数的增长,使得目标函数优化、参数估计、模型选择变得越来越困难,这类问题已普遍地影响到诸多领域,如机器学习[1]、图像处理[2]、模式识别[3]、文本分析[4]等,这种现象被称为维度灾难[5]。
维度灾难带来的问题主要表现在3个方面:(1)愈加增加的数据维数导致空间数据点分布更稀疏,使得空间的参数优化越来越棘手;(2)维数的升高使得高维数据索引组织效果变差,数据节点的重叠性呈指数级递增,导致数据检索时,增加过多的访问路径,造成检索效率低下;(3)高维数据处理对计算机的运算与存储能力要求较高,目前计算机的运算与存储能力仍不能完全满足其运算与存储要求。
上述问题给高维数据处理中的数据分析带来了重大挑战,同时维数的膨胀也给模式识别带来了较大的困难。为降低、消除维度灾难的影响,研究者提出了一系列的解决方法。为了准确把握降维技术的发展方向,本文研究了自2010年以来降维技术相关的大量国内外文献,结果表明,近年来越来越多的研究者开始致力于降维技术的研究并取得了可观的成果。
1 降维技术
降维技术旨在将高维数据映射到更低维的数据空间上以寻求数据紧凑表示,这种技术有利于对数据做进一步处理。例如在基于内容的图像检索中,将提取的高维图像特征向量数据通过降维处理降低到一定的维度,则可以使用相关的索引机制组织数据以进行更高效的检索。降维技术可用如下数学方式表达,设
(1)
其中,X为D维空间RD的一个数据集。通过降维技术找到一定的映射F:X→Y,使得
(2)
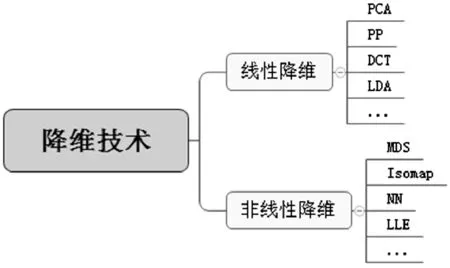
其中,Y为一个新的维度为d的数据集,且d 传统降维技术通常在处理较低维度的数据集时非常有效,而对较高维度的数据集则很难得出有意义的分析[6]。近年来,人们对降维技术的理论研究和技术应用等各个方面都取得了长足的进步,新的降维技术被不断提出,不同的技术各有所长,适用于不同的降维场景。 目前研究者已陆续提出了多种降维技术,如线性判别分析法[7]、主成分分析法[8]、多维尺度分析法[9]、等。本文依据映射形式的分类,将现有的降维技术分为线性降维和非线性降维,图1列出了典型的线性降维技术和非线性降维技术。 图1 降维技术分类 线性降维技术是出现最早的降维技术,特点是易于实现、快速简单、不存在局部极值与相对有效性,因此得到了广泛应用,下面介绍几种典型的线性降维技术。 1.2.1 主成分分析 主成分分析(Principal Components Analysis,PCA)[8]是一种坐标变化技术,通过将数据集映射到一组新变量(主成分)上,并设置数据方差的阈值以舍弃方差较少的主成分,新得到的维度(主成分)为原维度的线性组合,并尽可能反映数据原有的信息,以达到降维目的。缺点是在降维过程中,需要人工选取主成分个数,如果选取不当将导致信息丢失。 1.2.2 线性判别分析 线性判别分析(Linear Discriminant Analysis,LDA)[6]也称为Fisher判别分析,是一种有监督降维方法。LDA通过找寻数据集中的投影矩阵,可以将高维数据投影到低维空间中,并使数据集在低维空间中同类数据区别最小化,异类数据区别最大化。目前该方法主要应用于高维数据的分类工作,由于降维过程中不能灵活的调整分解矩阵的大小,在分类中心有重叠时会得到较差的分类效果。 线性降维技术通常不能在真实数据集的降维过程中较好地保持数据集的非线性特性,因此研究者提出了非线性降维技术。非线性降维技术通常情况下是基于线性降维技术进行非线性的扩展或采用神经网络等方法来进行优化降维,下面介绍几种典型的非线性降维技术。 1.3.1 多维尺度分析 多维尺度分析(Multi-Dimensional Scaling,MDS)[6]分为度量MDS和非度量MDS。度量MDS确保降维后低维数据点之间的距离与原数据点之间的相对距离尽量保持一致,以尽可能保留数据对象间的相似性,其降维过程中距离函数的选择具有灵活性。非度量MDS旨在确保降维前后数据对象间顺序关系一致性,而非数据对象间的相对距离。 1.3.2 局部线性嵌入 局部线性嵌入(Local Linear Embedding,LLE)[10]是一种突破传统降维方式的非线性降维模式,很多后续的流形学习和降维技术都与LLE有着紧密的联系。LLE的主要思想是将数据集视作是由大量相互邻接的局部线性块连接形成,这种局部线性块可以较好的描述原数据集的特征属性,从而实现降维。LLE的提出进一步地扩展了研究者关于降维的认识,并提出了一系列的LLE变体。如拉普拉斯特征映射(Laplacian Eigenmaps)[11]的主要思想是先将数据集中的数据点与其最近邻居连接构建一个邻居图,并对图的每条边赋予相应的权值,接着寻求数据集的嵌入坐标表示,保证嵌入坐标的平方距离最小,从而得到最优的低维表示向量。 随着降维技术的不断研究与应用,降维技术的理论框架已逐步形成。现有的降维技术已取得了可观的研究成果,近几年对于降维技术的研究,主要集中于原有算法的改进和延伸方面。 1.4.1 自适应线性数据降维技术 YN.Jeng等[12]基于元学习(Meta-learning)提出一种自适应线性数据降维算法。该算法针对数据的类型和特点,引入元学习和选择统计的方法作为数据集的构造和分类规则,以达到降维过程中的分类错误率。该算法的优点是适用于多种数据类型,且降维分类过程是是自适应的,缺点则是在处理含有较多异常值的数据集时性能较差。 1.4.2 基于统计相关的数据降维技术 A.Ramdas等[13]基于统计相关的方法,提出一种可应用最邻近分类的算法,该算法中提出的内在距离是其他扩散距离的概念相似,是变量间相关统计方法的拓展。该算法已应用于真实数据集中,相比其他统计相关算法具有更好的稳定性和分类效果。对于该算法中提出用于表示邻里演变的连接程度的参数t,其选取和理论解释不够明确,仍需要进一步进行试验验证。 1.4.3 其它降维技术 除了上述讨论的降维技术外,近年来还出现了多种降维技术。如线性降维方面的潜在语义索引(Latent Semantic Index,LSI)[14]、投影寻踪(Projection Pursuit,PP)[15]、子分析(Factor Analysis,FA)[16]、独立成分分析(Independent Components Analysis,ICA)[17]等方法。非线性降维方面则有核主成分分析(Kernel PCA,KPCA)[18]、等距映射(Isometric Mapping,Isomap)[19]、形[20]、局部线性协同(Locally Linear Coordination,LLC)[21]、Manifold Learning[22]等方法。 本文对几种典型高维数据降维技术的性能进行了分析整理,如表1所示。这些算法应用广泛,主要集中在分类和聚类领域。由于各算法的应用领域不同,使得性能优缺点差异较大,研究者需要根据实际情况进行适当的选择,并针对算法不足进行性能改进。 表1 典型降维技术性能 根据式(1)降维得到式(2),T(n)为时间复杂度,S(n)为空间复杂度,i为迭代次数,k为Isomap近邻点个数,w与m为Auto-encoder的权值和网络大小。 随着科技的进步,出现了越来越多复杂的真实数据,呈现给研究者处理分析相关数据及问题的挑战也愈加巨大。现有降维技术的研究为快速有效地处理高维数据提供了一定的便利,已经取得了较大的成果,但还有很多研究问题的处理效率有待提升。 目前流形学习方法[22]难以在应用上进行推广,原因在于该类方法并未建立高维流形数据与映射后低维数据之间的映射关系,使得无法获得新输入的高维数据与低维结果数据之间的映射表示。 目前降维技术在处理不同领域的较低维度数据(维度<50)时效率很好,但是在较高维度(维度>50)的处理效果仍有待提高。 目前降维技术对动态变化的数据集难以实现快速高效的降维,由于真实环境中数据的复杂性(非线性数据)与受噪声影响较大等原因,如何提高算法的鲁棒性,降低噪声和奇异值对数据的影响,提高降维算法的自适应性与降维结果的有效性是今后研究的重点。 本文围绕降维技术将高维数据中的降维问题分为线性降维和非线性降维,进行分类描述,介绍了近年来降维技术的研究成果,为更好的推广使用这些技术,对经典降维技术进行了性能分析,指出其优缺点。根据降维技术当前仍然存在的问题,展望了未来研究的方向。尽管降维技术原本是伴随着多媒体数据处理和数据挖掘中数据预处理这一领域出现的,但降维技术独特的理念给研究者在处理解决各类问题都提供了一个新的思路和方法,所以未来将产生更多的降维技术研究成果。 [1] Rosten E,Drummond T.Machine learning for high-speed corner detection[M].Berlin:Computer Vision-ECCV,Springer Heidelberg,2006. [2] Stommel M,Herzog O.SIFT-based object recognition with fast alphabet creation and reduced curse of dimensionality[C]. New Zealand: International Conference on Image and Vision Computing,2009. [3] Qin H,Tang S.A solution to dimensionality curse of BP network in pattern recognition based on RS theory[C].Sanya:International Joint Conference on Computational Sciences and Optimization,2009. [4] Gao M T,Wang Z O.A new algorithm for text clustering based on projection pursuit[C].Beijing:International Conference on Machine Learning and Cybernetics,IEEE,2007. [5] Erchtold S,B?hm C,Kriegal H P.The pyramid-technique: towards breaking the curse of dimensionality[J].ACM SIGMOD Record,1998,27(2):142-153. [6] Zhu X,Zhang S,Jin Z,et al.Missing value estimation for mixed-attribute data sets[J].IEEE Transactions on Knowledge & Data Engineering,2011,23(1):110-121. [7] Alavi A H,Gandomi A H.A robust data mining approach for formulation of eotechnical engineering systems[J]. Engineering Computations,2011,28(3):242-274. [8] 黄华盛,杨阿庆.基于PCA算法的人脸识别[J].电子科技,2015,28(8):98-101. [9] Rachev B,Smrikarov A.Proceedings of the 9th international conference on computer systems and technologies and workshop for PhD students in computing[C].Russia:International Conference on Computer Systems and Technologies and Workshop for Phd Students in Computing,ACM,2008. [10] Li B, Zhang Y. Supervised locally linear embedding projection (SLLEP) for machinery fault diagnosis[J].Mechanical Systems & Signal Processing,2011,25(8):3125-3134. [11] Wang J.Geometric structure of high-dimensional data and dimensionality reduction[M].Berlin:Springer Heidelberg,2012. [12] Jeng Y N,Lin S Y,Lee Z S. Smoothing of the multiple one-dimensional adaptive grid procedure[J].Aiaa Journal,2015, 38(38):2353-2355. [13] Ramdas A, Reddi S J, Poczos B, et al. Adaptivity and computation-statistics tradeoffs for kernel and distance based high dimensional two sample testing[J]. Statistical Applications in Genetics & Molecular Biology,2015,12(6):1-12. [14] Zheng W. Dimensionality reduction by combining category information and latent semantic index for text categorization[J].Journal of Information & Computational Science,2013, 10(8):2463-2469. [15] Schimek M G.Projection pursuit regression[M].NewYork:John Wiley & Sons,Inc.,2012. [16] Cady B, Sedgwick C E, Meissner W A,et al.Risk factor analysis in differentiated thyroid cancer[J].Cancer, 2015,43(43):810-820. [17] Lacerda G,Spirtes P L,Ramsey J,et al. Discovering cyclic causal models by independent components analysis[C].Grace:Uncertainty in Artificial Intelligence,2012. [18] Alzate C,Suykens J A K.Multiway spectral clustering with out-of-sample extensions through weighted kernel PCA[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2010,32(2):335-347. [19] Zhang N,Tian X M.Nonlinear dynamic fault detection method based on isometric mapping[J].Journal of Shanghai Jiaotong University,2011,45(8):1202-1206. [20] Zhang Z,Chow T W S,Zhao M. Trace ratio optimization-based semi-supervised nonlinear dimensionality reduction for marginal manifold visualization[J].IEEE Transactions on Knowledge & Data Engineering,2013,25(5):1148-1161. [21] Hong Huang,Jianwei Li,Hailiang Feng. Subspaces versus submanifolds:a comparative study in small sample size problem[J].International Journal of Pattern Recognition & Artificial Intelligence,2011,23(3):463-490. [22] Saini S,Rambli D R B A,Sulaiman S B,et al.Markerless multi-view human motion tracking using manifold model learning by charting[J].Procedia Engineering,2012(41):664-670.1.1 常见降维技术
1.2 线性降维技术
1.3 非线性降维技术
1.4 近年推出的降维技术
2 性能分析

3 未来研究方向
3.1 流形学习降维
3.2 超高维数据降维
3.3 自适应能力
4 结束语
