毛细管内气-液Taylor流动换热特性数值模拟

周乃香, 张井志, 林金品, 李 蔚

(1. 山东省城乡规划设计研究院,山东 济南 250013; 2. 浙江大学 能源工程学院,浙江 杭州 310027)



毛细管内气-液Taylor流动换热特性数值模拟

周乃香1, 张井志2, 林金品2, 李 蔚2

(1. 山东省城乡规划设计研究院,山东 济南 250013; 2. 浙江大学 能源工程学院,浙江 杭州 310027)

采用动网格技术,对恒壁温边界下,竖直上升毛细管(管径为1 mm)内充分发展状态的气-液Taylor流动进行数值研究,分析入口雷诺数、气泡体积分数对Taylor流动的换热阻力特性的影响.模拟结果表明,由于Taylor气泡的存在,液柱区域的摩擦阻力因子高于单相流动,模拟结果与经验公式吻合较好.液柱表观努赛尔特数随气泡体积分数的增大而增大,基本不随入口雷诺数的变化而改变.在恒壁温边界下,Taylor气泡及液膜区域对整体传热的贡献较小.液柱区域内循环可以提高加强核心区域与近壁面区域的热量交换,加快换热过程,提高Taylor流动的传热效果.内循环对换热的强化作用随着液柱长度的增大而降低.

Taylor流动；毛细管；压降；传热

Taylor流动是一种典型的无相变两相流动,特征如下：Taylor气泡长度大于通道管径；气泡与壁面之间存在一层很薄的液膜；两个连续的气泡内为连续相的液柱.由于Taylor气泡的存在,液柱区域会产生由通道中心到壁面的内循环,该内循环的存在可以强化Taylor流动的传热传质特性.相对相变流动如沸腾、蒸发等,无相变的Taylor流动更加稳定、可控,可以应用于微反应器、微电子器件散热等领域.

对于Taylor流动的实验研究,主要集中于气泡形态[1]、气泡速度[2]、液膜厚度[3]以及压降损失[4]等,对传热特性的研究相对较少.Leung等[5]研究2 mm圆管内的氮气-水Taylor流动换热特性,指出液柱区域Nu主要与无量纲的液柱长度有关,并提出Nu的关联式.Walsh等[6]利用红外热像技术分析恒热流边界下Taylor流动的温度场,结果表明,相对于单相流动,Taylor流动可以大幅提高对流换热系数.Lim等[7]研究恒热流条件下微小通道内气-液Taylor流动的换热阻力特性,指出当气泡直径与通道直径相当时,换热系数可以提高178%,而压降仅提高27%.

相对实验研究,数值模拟可以较好地获得Taylor流动的速度、温度场,分析Taylor流动的换热阻力特性.Gupta等[8]研究0.5 mm微通道内的Taylor流动,结果表明,Nu随气相分数的增大而降低,基本不随Re的增大而改变.Zhang等[9]分析了圆管内Taylor流动换热情况,结果显示,壁面局部换热系数在液柱区域沿流动方向逐渐增大,在气泡区域沿流动方向逐渐降低.Mehdizadeh等[10]的模拟结果表明,液膜区域对Taylor流动换热阻力特性有重要的作用.Asadolahi等[11]利用动网格技术,研究充分发展状态下Taylor流动的换热特性,相对于固定计算域,该方法可以大幅降低计算时间.Talimi等[12]忽略气相的影响,研究方形通道的液柱区域的流动换热情况,采用该方法得到的换热系数高于实验值.Che等[13]研究恒热流条件下液柱区域的换热特性,指出Taylor流动可以提高换热系数、降低壁面温度.张井志等[14-15]对微小通道内Taylor流动的流动压降特性进行数值研究,结果表明,Taylor气泡的形状、液膜厚度和尾部波动区域基本不随含气率改变而变化.

微通道内的Taylor流动已有一定的实验模拟结果,但充分发展Taylor流动的流动换热特性分析有一定的不足.相对于固定计算域,移动计算域的方法可以节约计算资源,更容易获得充分发展的Taylor流动.本文采用Asadolahi等[11]的动网格技术研究竖直毛细管内(dh=1 mm)Taylor流动的换热阻力特性,并分析恒壁温边界下,Taylor流动动态换热过程.

1 数值计算模型

采用ANSYS Fluent 14.5 内置的VOF模型捕捉Taylor流动的气-液界面.VOF模型假设气-液两相无法互相渗透,在连续性、动量、能量方程的基础上,求解体积分数方程,获得计算域内的气-液分布.

1.1 数学模型

计算区域流体控制方程如下.

连续性方程为

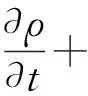
(1)

动量方程为

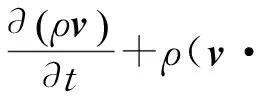
(2)

能量方程为

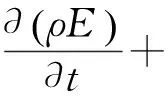
(3)

体积分数方程为

(4)

式中：ρ为混合相密度,

ρ=φlρl+φgρg;

(5)

μ为混合相黏性系数,

μ=φlμl+φgμg;

(6)

κ为导热系数,

κ=φlκl+φgκg;

(7)

φ为体积分数,下标l、g分别表示液相和气相,

φl+φg=0；

(8)

v为速度矢量；p为压力；g为重力加速度；F为体积力.

1.2 计算模型及边界条件

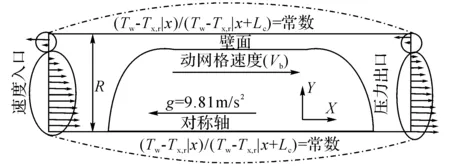
图1 计算域及边界条件Fig.1 Computational domain and boundary conditions

如图1所示,计算域采用二维轴对称模型,长度固定为10 mm,轴向方向为X轴方向.入口指定为速度入口边界,出口为压力出口边界,主流方向由速度入口指向压力出口.壁面采用无滑移的等温壁面,壁面温度为310 K,对称轴采用轴边界条件.在模拟过程中,液相为水,气相为空气,采用恒物性.在计算过程中,首先求解流动与体积分数方程,在获得稳定的速度场及气泡形状后,取消速度场与体积分数方程的求解,仅求解温度场.该方法广泛应用于单相充分发展状态下流动温度场的数值分析,相对耦合求解,可以节约计算时间.

计算域采用动网格模型,其中网格的移动速度为气泡的速度,以保证气泡一直处于计算域中间位置.在初始时刻,将整个计算域设定为圆管管内充分发展的轴向速度.利用用户自定义函数(UDF)将压力出口处的速度分量赋予速度入口.当气泡速度与进出口压差不随计算迭代而变化时,认为Taylor流动的流动场稳定.在获得稳定的流动场以后,初始化计算域的温度为300 K, 取消连续性方程、动量方程及体积分数方程的求解.通过UDF将出口温度分量赋予入口,进出口的温度分量关系如下所示：

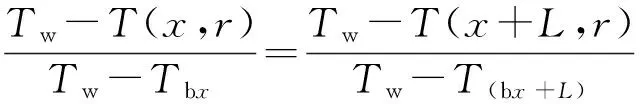
(9)

1.3 网格划分及无关性验证

计算域采用结构网格进行划分,对壁面附近进行加密以捕捉壁面与Taylor气泡之间的液膜,Gupta等[8]指出在液膜区域至少需要布置5层网格才可以精确捕捉液膜厚度.如图2所示为网格的无关性检测.可知,在3种网格数目下,Taylor气泡的形状基本一致.当网格数目较小时,Taylor气泡长度相对较长而液膜区域相应变厚.考虑计算时间,最终选择的网格尺寸为95×1 540(径向数目×轴向数目).

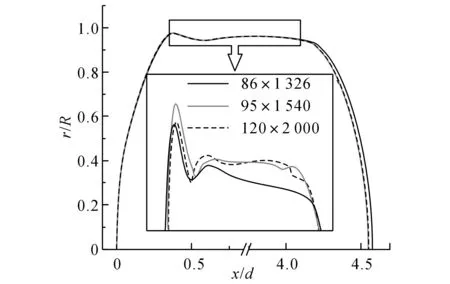
图2 3种网格尺寸下的Taylor气泡形状Fig.2 Shapes of Taylor bubble obtained from three meshes

2 模拟结果及数据分析

为了研究恒壁温边界下Taylor流动的压降、换热变化规律,分析竖直毛细管(dh=1 mm)内气泡体积分数φb=0.4时、入口Re=200～600和Re=400、φb=0.3～0.55情况下,Taylor流动的流动换热特性,其中Re、φb的定义为

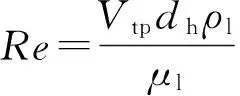
(10)

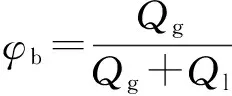
(11)

式中：Re为入口雷诺数,Vtp为入口两相速度,Q为体积.

2.1 壁面压力分布

如图3所示为壁面压力沿轴向的分布情况,其中阴影部分代表Taylor气泡区域.由图3可得,在液柱区域,壁面压力沿轴向线性下降,压力分布特性与充分发展的管内流动类似.在气泡尾部区域,由于维持气泡稳定需要气-液两相间存在压力梯度,压力有一定的波动.在液膜区域,壁面压力保持稳定,基本不随x/d的变化而改变.在靠近气泡头部位置,在气-液两相表面压力差的作用下,会有一定的压力下降,相对于气泡尾部区域,该部分区域的压力波动更小.

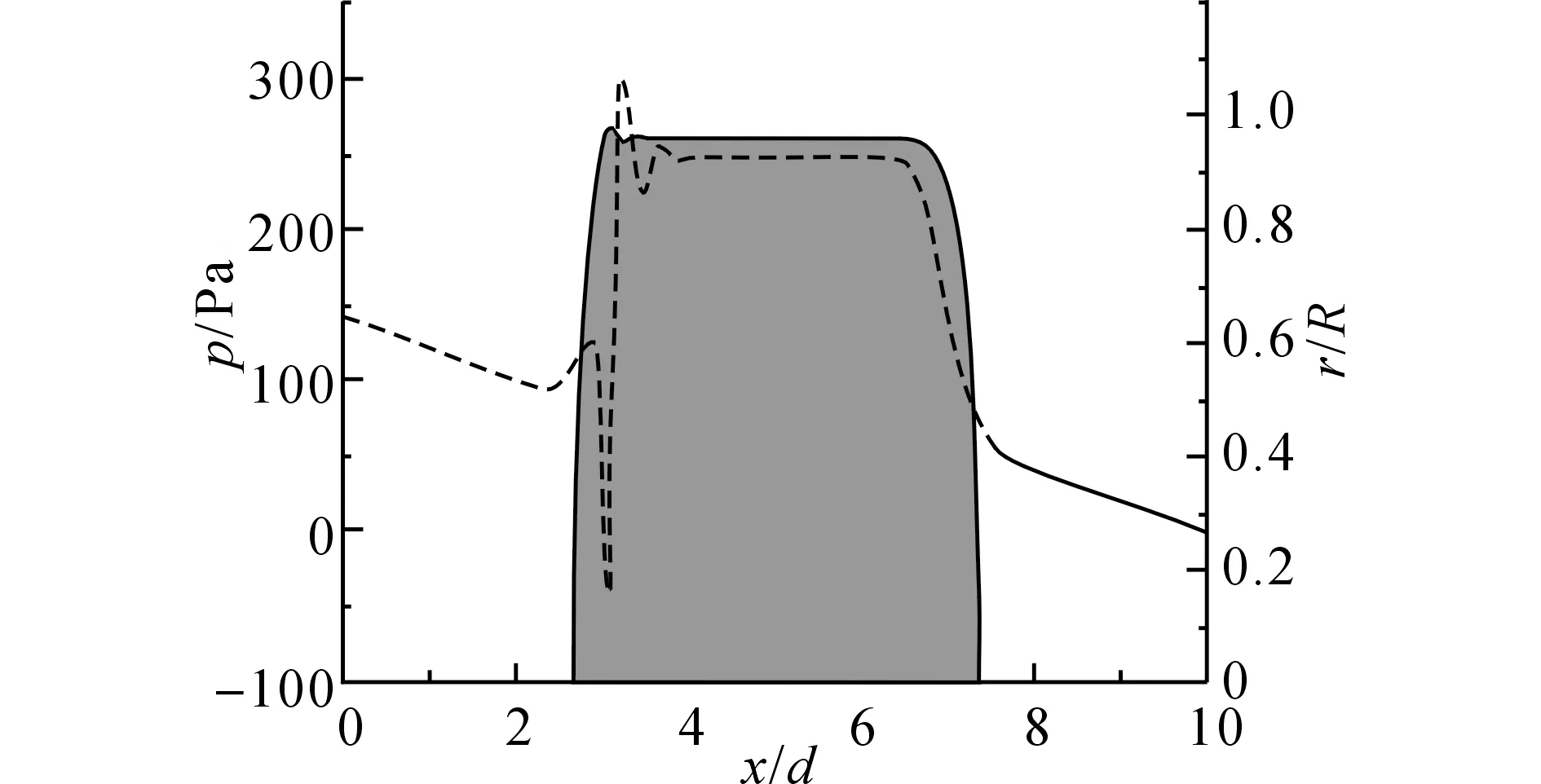
图3 壁面压力沿轴向的分布Fig.3 Distribution of pressure at tube wall along axialdirection

2.2 摩擦阻力因子

Kreutzer等[4]讨论了惯性力和表面张力对Taylor流动的影响,得到液柱区域摩擦阻力因子的表达式：

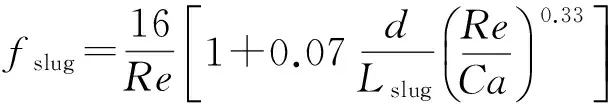
(12)

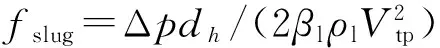
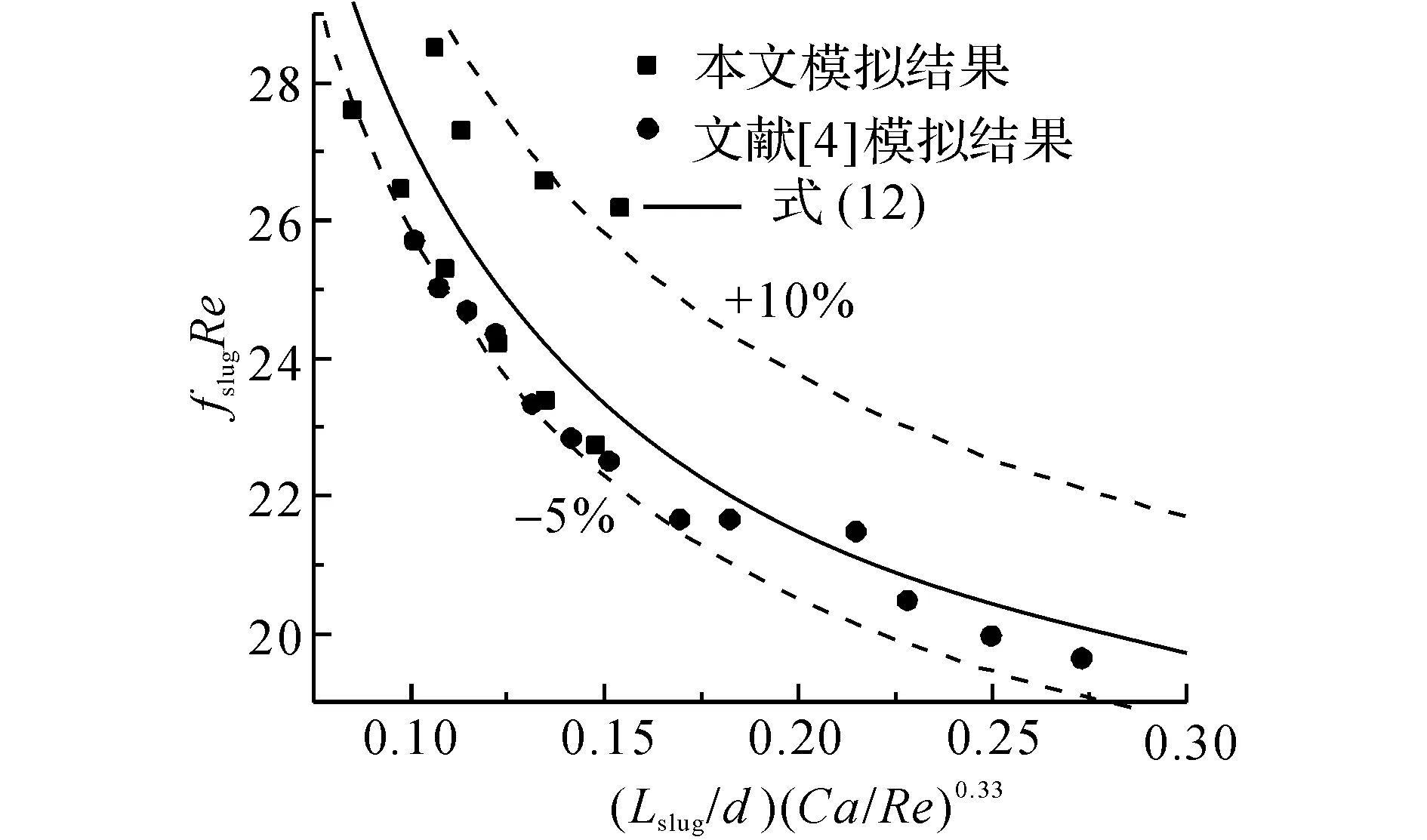
图4 fslugRe随(Lslug/d)(Ca/Re)0.33的变化规律Fig.4 fslugRe as function of (Lslug/d) (Ca/Re)0.33

如式(12)所示,当液柱长度趋于无穷大时,Taylor气泡的影响可以忽略,摩擦阻力与圆管内单相层流的充分发展表达式一致.如图4所示为式(12)预测值与文献[4]及本文模拟结果的对比.由图4可得,fslugRe随无量纲液柱长度的增长而降低.利用式(12)可以较好地预测本文模拟结果的趋势,模拟结果与预测值的相对误差小于10%.

2.3 换热特性

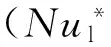
图随Re、φb及时间的变化规律Fig.

(13)

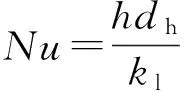
(14)

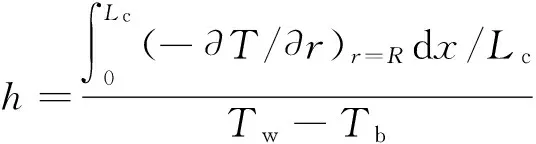
(15)

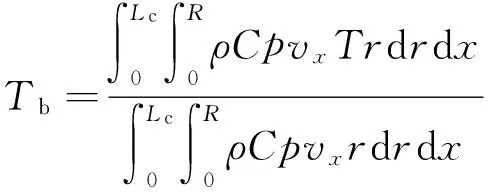
(16)

式中：Nu为计算域平均努塞尔特数,h为计算域平均换热系数,Lc为计算域长度,Ll为液柱长度,Tb为流体平均温度,r、x为径向、轴向坐标.

图6 局部Nu沿轴向的分布Fig.6 Distribution of local Nu along axial direction

如图6所示为Re=400、φb=0.4时Taylor流动局部Nu随时间的变化规律,其中16、70 ms对应于第一、第二极小值点,30 ms对应于第一个极大值点.由图6可得,气泡区域对整个计算域的换热贡献较小,主要由于气体的密度与比热容的乘积较小,更容易被加热,导致壁面附近的温度梯度基本为0,从而该部分区域的换热量较小.由式(15)可得,此处的换热系数较低.在液柱区域,Nu沿轴向逐渐上升,气泡前部液柱区域的Nu高于Taylor气泡尾部后的液柱区域.在30 ms以后,两者之差逐渐降低,Nu逐渐趋于稳定,换热达到充分发展.

图7 η随Re、φb及时间的变化规律Fig.7 Effects of Re, φb and time on heat transfer index η

如图7所示为传热指数η随时间的变化规律,其中传热指数的定义为由起始时刻到t时刻壁面导入的热量与流体温度与壁面温度相同时的最大传热量之比.η的定义如下：

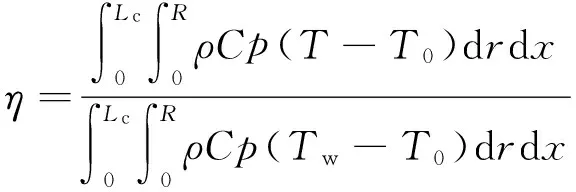
(17)

式中：T0为计算域初始温度,本文设定为300 K.

由图7(a)可得,η随t的增大而逐渐上升,最终趋于1.0.η随t的变化斜率随着Re的增大而逐渐降低,在低Re数下,流体可以更快地被加热至接近壁温状态,更容易充分发展.由图7(a)可得,相对于Re,φb对η的影响较小,η随t的变化斜率随φb的增大而降低.

2.4 温度云图与径向温度分布

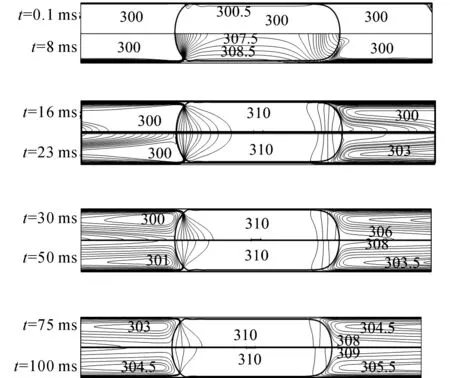
图8 Taylor 流动内温度云图随时间的变化Fig.8 Temperature contour in Taylor flow

如图8所示为8个时刻计算域内的温度分布情况.由图8可得,在加热初始阶段,气泡与液柱区域会产生很薄的温度边界层,壁面温度梯度最大,换热量最高.随着时间的增长,由于气相热容较小,更容易吸收热量,气泡区域首先升高温度,接近壁面温度,导致液膜区域温度梯度降低,换热系数减小,如t=0.1 ms所示.随着时间的推进,液柱区域的温度边界层逐渐变厚,传热量降低.如t=16 ms和t=23 ms可得,在靠近气泡头部区域附近的液柱区域,心轴附近的液体首先被加热,而后靠近气泡尾部区域液柱核心区域的温度逐渐上升.当t=100 ms时,气泡区域温度基本为壁面温度,液柱区域轴线与壁面附近温度较高,靠近径向中心位置,温度相对较低.

为了更好地解释温度的变化情况,将计算域的流线与温度云图结合起来分析,如图9所示.由图9(a)可得,在气泡头部附近的区域,相对流线由壁面指向核心区域,气泡尾部附近的区域为由核心区域指向壁面.在传热过程中,靠近壁面的热流体会首先被带入核心区域,然后在液柱区域的内循环中逐渐加热核心区域的流体,到达下一个气泡尾部区域,受到气泡的阻挡,流向壁面区域.整个液柱区域的内循环可以提高传热速率,减小系统到达热稳定所需的时间,同时内循环可以提高加强核心区域与近壁面区域的热量交换,提高Taylor流动的传热效果.在模拟过程中,仅考虑气-液Taylor流动,由于两相比热容之差太大,气泡区域的内循环对整个换热过程的影响较小；对于液-液两相流情况,离散相的Taylor液滴内的循环会对整个传热过程产生一定的影响.

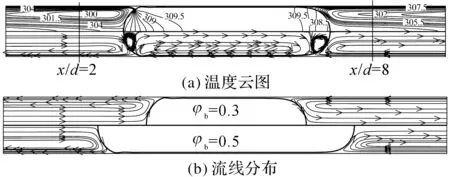
图9 Taylor流动内温度云图及流线分布Fig.9 Distribution of temperature contours and stream traces in Taylor flow

液柱区域靠近Taylor气泡附近的径向流动对整个换热的贡献较大,由场协同理论[16]可知,沿径向的流动速度可以减小速度矢量与温度梯度的夹角,进而强化传热过程.如图9(b)可得,随着φb的增大,液柱区域的长度逐渐降低,内循环中平行于通道轴向的区域所占的比例逐渐降低,而沿径向流动区域的比例增大,进而增大液柱表观Nusselt数.内循环对液柱区域换热的强化随着液柱长度的增大而降低,对于长度趋于无穷大时,液柱区域的换热效果基本与单相层流充分发展一致.对于恒壁温边界条件,气泡区域对换热的贡献较小,导致平均Nusselt数随φb的增大而降低.

如图10所示为8个时刻,x/d=2和x/d=8径向的温度分布情况.由图10可得,在r/R接近0.7的位置,流体温度较低,x/d=8位置的温度高于x/d=2区域.近壁面区域的温度梯度随着时间的增大而逐渐降低,x/d=2区域的温度梯度更高,换热系数更高.当t=30 ms时,在气泡尾部区域附近的液柱内,流体的温度边界层发展较慢,其值与16 ms时一致,导致t=30 ms时,平均Nu得到极大值.随着时间的增大,x/d=2与x/d=8核心区域的流体温度之差逐渐缩小,流体平均温度逐渐上升.由于壁面温度梯度的降低,平均Nu趋于定值.

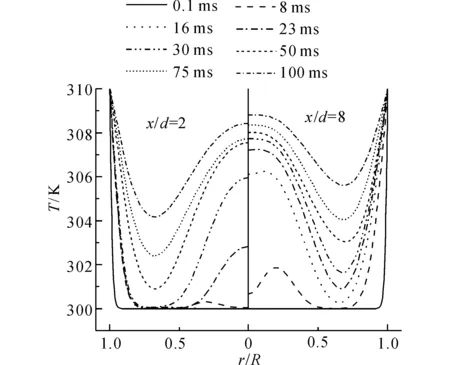
图10 径向温度分布随时间的变化Fig.10 Distribution of radial temperature at varying time

3 结 论

(1)壁面压力沿着轴向逐渐降低,Taylor流动液柱区域的压力分布与充分发展的单相层流流动对应的压力分布类似.

(2)由于Taylor气泡的存在,液柱区域的摩擦阻力因子高于单相情况,fslugRe主要与(Lslug/d)×(Ca/Re)0.33相关.Kreutzer等[4]的经验公式可以较好地预测本文的模拟结果.

(3)液柱表观Nu数随φb的增大而增大,在稳定时基本不随Re的变化而改变.传热指数η随t的变化斜率随着Re与φb的增大而降低,在低Re数下,换热过程更容易充分发展.

(4)液柱区域的内循环可以提高加强核心区域与近壁面区域的热量交换,提高Taylor流动的传热效果,内循环对换热强化的作用随着液柱长度的增大而逐渐降低.

[1] ZHAO T S, BI Q C. Co-current air-water two-phase flow patterns in vertical triangular microchannels [J]. International Journal of Multiphase Flow, 2001, 27(5): 765-782．

[2] LIU H, VANDU C O, KRISHNA R. Hydrodynamics of Taylor flow in vertical capillaries: flow regimes, bubble rise velocity, liquid slug length, and pressure drop [J]. Industrial and Engineering Chemistry Research, 2005, 44(14): 4884-4897．

[3] HAN Y, SHIKAZONO N. Measurement of the liquid film thickness in micro tube slug flow [J]. International Journal of Heat and Fluid Flow, 2009, 30(5): 842-853．

[4] KREUTZER M T, KAPTEIJN F, MOULIJN J A, et al. Inertial and interfacial effects on pressure drop of Taylor flow in capillaries [J]. AIChE Journal, 2005,51(9): 2428-2440．

[5] LEUNG S Y, LIU Y, FLETCHER D F, et al. Heat transfer in well-characterised Taylor flow [J]. Chemical Engineering Science, 2010, 65(24): 6379-6388．

[6] WALSH P A, WALSH E J, MUZYCHKA Y S. Heat transfer model for gas-liquid slug flows under constant flux [J]. International Journal of Heat and Mass Transfer, 2010, 53(15/16): 3193-3201．

[7] LIM Y S, YU S M, NGUYEN N T. Flow visualization and heat transfer characteristics of gas-liquid two-phase flow in microtube under constant heat flux at wall [J]. International Journal of Heat and Mass Transfer, 2013, 56(1/2): 350-359．

[8] GUPTA R, FLETCHER D F, HAYNES B S. CFD modelling of flow and heat transfer in the Taylor flow regime [J]. Chemical Engineering Science, 2010,65(6): 2094-2107．

[9] ZHANG J, LI W. Investigation of hydrodynamic and heat transfer characteristics of gas-liquid Taylor flow in vertical capillaries [J]. International Communications in Heat and Mass Transfer, 2016, 74: 1-10．[10] MEHDIZADEH A, SHERIF S A, LEAR W E.Numerical simulation of thermofluid characteristics of two-phase slug flow in microchannels [J]. International Journal of Heat and Mass Transfer, 2011, 54(15/16): 3457-3465．

[11] ASADOLAHI A N, GUPTA R, LEUNG S Y, et al. Validation of a CFD model of Taylor flow hydrodynamics and heat transfer [J]. Chemical Engineering Science, 2012, 69(1): 541-552．

[12] TALIMI V, MUZYCHKA Y S, KOCABIYIK S. Slug flow heat transfer in square microchannels [J]. International Journal of Heat and Mass Transfer, 2013, 62: 752-760．

[13] CHE Z, WONG T N, NGUYEN N T. Heat transfer in plug flow in cylindrical microcapillaries with constant surface heat flux [J]. International Journal of Thermal Sciences, 2013, 64: 204-212．

[14] 张井志,李蔚.微小管径圆管气-液Taylor流动数值模拟[J].浙江大学学报：工学版, 2015, 49(8): 1572-1577．

ZHANG Jing-zhi, LI Wei. Numerical simulation of gas-liquid Taylor flow in mini/micro tubes [J], Journal of Zhejiang University: Engineering Science, 2015,49(8): 1572-1577．

[15] 张井志,李蔚.毛细管内气液Taylor流动的气泡及阻力特性[J].化工学报, 2015, 66(3): 942-948．

ZHANG Jing-zhi, LI Wei. Bubble and frictional characteristics of gas-liquid Taylor flow in capillary tube [J]. CIESC Journal, 2015, 66(3): 942-948．

[16] 过增元.换热器中的场协同原则及其应用[J].机械工程学报,2003, 39(12): 1-9．

GUO Zeng-yuan. Principle of field coordination in heat exchangers and its applications [J]. Chinese Journal of Mechanical Engineering, 2003, 39(12): 1-9．

Numerical investigation on heat transfer and hydrodynamic characteristics of gas-liquid Taylor flow in capillaries

ZHOU Nai-xiang1, ZHANG Jing-zhi2, LIN Jin-pin2, LI Wei2

(1,ShandongUrbanandRuralPlanningandDesignInstitute,Jinan250013,China;2.CollegeofEnergyEngineering,ZhejiangUniversity,Hangzhou310027,China)

Numerical work of fully developed gas-liquid Taylor flow in vertical upward capillaries with inner diameter of 1 mm under isothermal wall boundary condition was performed with the dynamic mesh model. The effects of inlet Reynolds number and gas void fraction on thermal and flow characteristics of Taylor flow were discussed. Results indicate that the friction factor in the liquid slug is higher than that of single-phase flow, and the empirical correlation can predict the numerical data well. The apparent liquid slug Nusselt number increasing with increasing gas void fraction and remains nearly constant with increasing inlet Reynolds number. The Taylor bubble and the thin liquid film region have insignificant contribution to the overall heat transfer coefficients in Taylor flow under isothermal wall boundary condition. The inner recirculation in the liquid slug region can improve the heat transfer between the tube wall and the core region, accelerate the heat transfer process, and enhance the heat transfer performance in Taylor flow. The effect of inner recirculation on heat transfer enhancement decreases with increasing liquid slug length．

Taylor flow; capillaries; pressure drop; heat transfer

2015-09-09.

国家自然科学基金重大国际合作项目(51210011)；浙江省自然科学基金资助项目(LZ13E060001).

周乃香(1987— ),女,硕士,工程师,从事强化传热与节能技术研究.ORCID: 0000-0003-3061-230X.

E-mail: queenznx@163.com

李蔚,男，教授.ORCID: 0000-0002-2295-2542.E-mail: weili96@zju.edu.cn

10.3785/j.issn.1008-973X.2016.10.004

TK 124

A

1008-973X(2016)10-1859-06

浙江大学学报(工学版)网址： www.zjujournals.com/eng