组合同伦法求一般非线性规划问题

黄青群

（河池学院数学与统计学院，广西 宜州 546300）

组合同伦法求一般非线性规划问题

黄青群

（河池学院数学与统计学院，广西 宜州 546300）

文章把含有等式约束和不等式约束的一般非线性规划问题转化为只有不等式约束的非线性规划问题，然后构造一个新的同伦方程，与牛顿法结合得到一个新的同伦算法，在变形锥条件下，证明了算法的全局线性收敛性。

组合同伦；一般凸规划；全局收敛性；牛顿法

1 引言

同伦算法是大范围的收敛算法，它是求解非线性方程组的一种新途径。由于非线性方程组的复杂性，导致很难直接求得其相应的解，此时可以构造一个相对容易求解的方程组，从求解后者的解出发，通过路径跟踪从而求得前者的解。这就是同伦算法的基本思路。同伦算法已经应用到了不同的非线性规划问题，如线性互补问题[1]、多目标优化问题[2]、均衡规划问题[3]等等。本文把含有等式约束和不等式约束的一般非线性规划问题转化为只有不等式约束的非线性规划问题，然后构造一个新的同伦方程，与牛顿法结合得到一个新的同伦算法，在变形锥条件下，证明了算法的全局线性收敛性。

考虑一般非线性规划问题(GNLP)：

充分光滑的凸函数。由文献[4]知可将问题(1)转化为问题(2)进行求解：

问题(2)的KKT系统为：

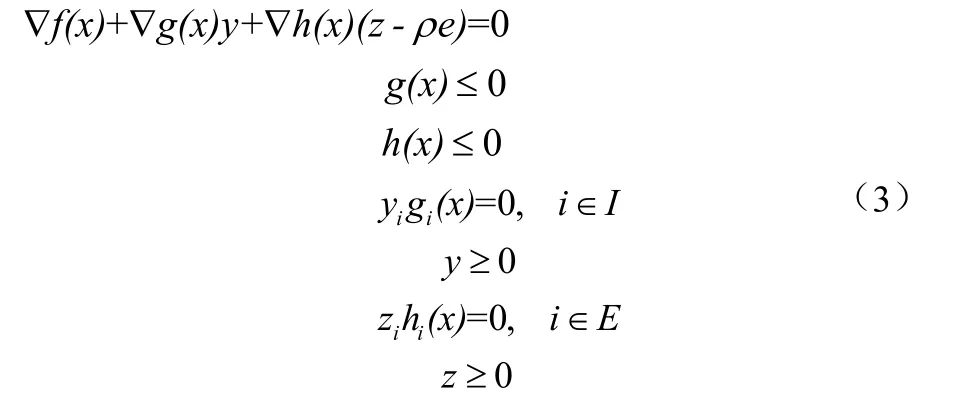
目前为止，很多文献在“法锥条件”、“弱法锥条件”、“拟法锥条件”或“伪法锥条件”下证明了同伦路径的存在性以及收敛性。本文在变形锥条件下证明同伦路径的存在性以及收敛性，该条件比“法锥条件”、“弱法锥条件”、“拟法锥条件”及“伪法锥条件”更容易满足。

为了求解问题(2)，构造同伦方程：

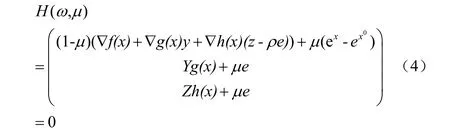
作如下的假设：

(A1)Ω0非空有界；

(A2)∀ x ∈Ω，矩阵{∇ g i(x):i∈ B(x);∇hi(x):i∈E}列满秩；

(A3)(变形锥条件【5】) 设 T(x,x0):Rn→ Rn是二次连续可微的，满足：

（1）对任意的 x0,T = 0当且仅当 x = x0；

（2） ∀y∈ Rm,x ∈∂Ω，若 T(x,x0) ≠ 0，则

其中I(x) ={i ∈{m + 1,6 ,m + r}:hi(x ) =0}。

（3）对任意的 x0，矩阵是列满秩的。

本文结构如下，第2节给出了β-锥邻域的定义以及算法的基本框架，第3节给出了算法的全局线性收敛性证明。

2 算法

同伦方法主要是在 β-锥邻域内通过追踪同伦路径从而得到原方程的解，所以首先给出β-锥邻域的定义：

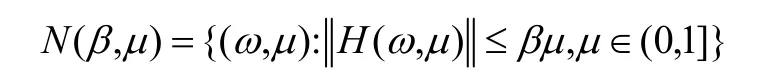
称 N (β ,μ)为β-锥邻域，β＞0称为为邻域半径。下面引理说明β-锥邻域在可行域内部。

引理1[4]设 y＞ 0,z＞o,β ∈ (0,1)则有

下面给出本文算法。

算法:

步0.(初始化)

令

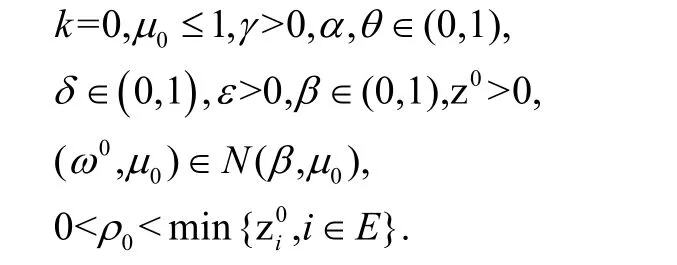
步1.(终止条件)

若μ ＜ε，则算法停止,ωk=(xk,yk,zk)T即为问题(4)的

k解。

步2.(更新参数 ρk)

计算

取

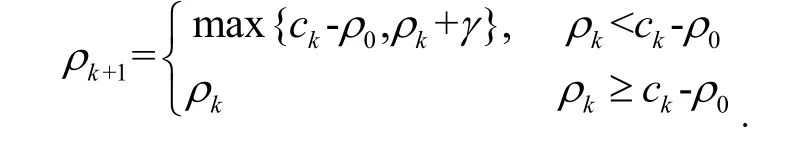
步3.(计算牛顿方向)

固定 μk，求解线性方程组

得

步4.(线性搜索)

取 λk为 1, δ, δ2,6中的最大值，使之满足

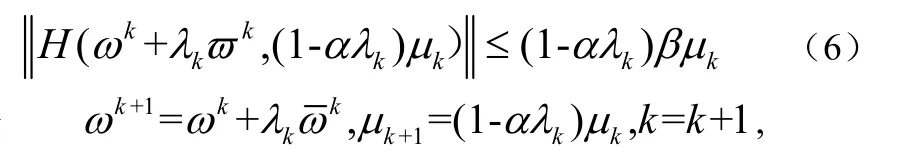
令

返回步1。

引理2 如果 f(x),gi(x),i∈ I,hi(x),i∈ E 是充分光滑的凸函数，初始点 ω0∈Ω0× R+m

+

× R+

r+，那么对于任意μ∈ (0,1],(ω,μ) ∈ N(β,μ) ,H'(ω,μ)是非奇异矩阵。

ω

证 通过计算整理，有

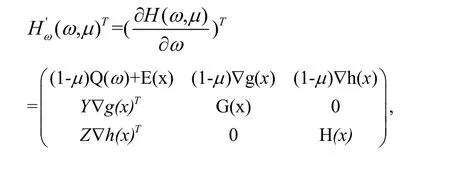
其中

有

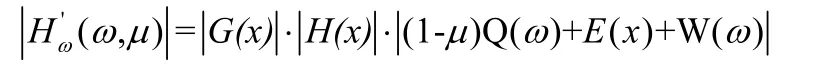
由于 f(x),g(x),i∈ I,hi(x),i∈ E 是充分光滑的凸函数，所以∇2f(x), ∇2gi(x), ∇2hi(x)是半正定矩阵，又从算法可得yi＞0,i ∈I,zi-ρ＞0,i∈ E ，于是 Q(ω)为半正定矩阵，因为Y,Z,E(x)是正对角矩阵，通过计算知 W (ω)也是半正定矩阵，故对任意 μ∈ (0,1],(ω,μ) ∈ N(β,μ)，有(1-μ)Q( ω)+ E(x)+W(ω)为正定矩阵，G(x),H(x)为非奇异矩阵。所以亦即为非奇异矩阵。

定理1 算法是良定的。

证 由引理2及算法中的(5)知 Hω'(ω,μ)是非奇异的,于是方程组(5)有唯一解，所以算法的步3良定。由文献[4]知，存在整数c1,c2,c3，当时(6)成立，于是算法的步4良定。综上可得整个算法是良定的。

3 算法的全局收敛性

为证明算法全局线性收敛性给出以下假设：

H3.1 由算法产生的序列{ωk}有界，且其聚点满足严格互补条件。

引理5说明了问题(1)与问题(2)之间的关系。

引理5[4]设ρ为给定值，若x是问题(2)的KKT点，则x是问题(1)的KKT点。

引理 6[4]存在正整数 k0，使得对所有 k≥k0，有ρk≡ ρk0≡ ρ,k∈K 。

下面证明算法的全局线性收敛性。

定理2 设算法产生的无穷序列为{(ωk,μk)}，那么下列结论成立

（1）对于 k= 0,1,2,···

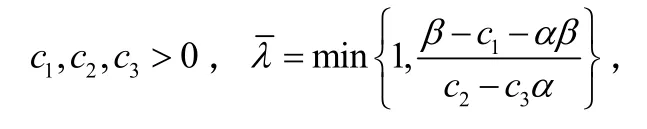
故{μk}全局收敛于0。

（4）序列{ωk}线性收敛到问题(4)的解，即{xk}线性收敛到问题(2)的解，从而得到问题(1)的解。

证

（1）对k进行数学归纳法证明。当k=0时，由算法的步0可知结论成立.假设对任意的k＞0结论都成立，那么对于k+1，根据β-锥邻域的定义及算法的步骤4有而而且

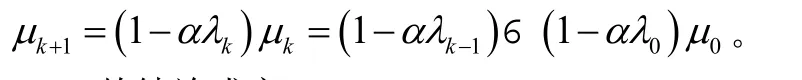
故结论成立。

（2）根据定理1中对步骤4良定性的证明过程可知，对任意k≥0，有其中于是

所以{μk}全局收敛于0。

（3）根据同伦方程(4)可知，存在常数 c4＞ 0，使得因此有

（4）根据由算法可得

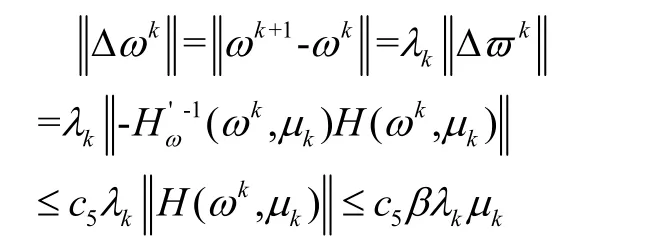
这说明{ωk}是一个Cauchy序列而且收敛到一点ω*，因为(ωk,μk)∈N (β,μk)所以ω*为(4)的一个解，亦即 x*为问题(2)的解，从而也就是问题(1)的解。

[1] 杨丹丹,韩海山,李园.基于不动点迭代法解线性互补问题[J].内蒙古民族大学学报(自然科学版),2014,29(4):388-389.

[2] 贺莉,谭佳伟,陈嘉,等.混合约束多目标优化问题的凝聚同伦内点方法[J].吉林大学学报(理学版),2014,52(2):212-218.

[3] 何非,商玉凤,梁心,等.半内点同伦方法解均衡规划问题[J].吉林大学学报(理学版),2014,52(3):470-474.

[4] Q. Huang, Zh.Zhu,X.Wang.A predictor-corrector algorithm combined conjugate gradient with homotopy interior point for general nonlinear programming[J].Applied Mathematics and Computation,2013(219):4379-4386.

[5] 张珊.非线性规划的同伦内点方法[D].长春:吉林大学, 2008.

Combined homotopy method for general nonlinear programming problem

This paper transfers the general nonlinear programming with equality constraints and inequality constraints problem into a nonlinear programming problem with inequality constraints only, and then constructs a new homotopy equation, finally combines with Newton's method to get a new homotopy algorithm. Under the condition of deformation cone, it proves the global linear convergence of the algorithm.

Combined homotopy; general convex programming; global convergence; Newton’s method

O232

A

1008-1151(2016)07-0132-03

2016-06-11

广西高校科研项目（2013LX120）；河池学院教改课题（2014EB019）；河南省高校重点科研项目（17A110032）。

黄青群（1980－），女，广西梧州人，河池学院数学与统计学院讲师，硕士，研究方向为优化理论与算法。