并行分布式遗传算法的研究
2016-12-02何文静
何文静
(广西大学计算机与电子信息学院,广西 南宁 530004)
并行分布式遗传算法的研究
何文静
(广西大学计算机与电子信息学院,广西 南宁 530004)
传统遗传算法在面对一些搜索空间巨大的复杂问题时,其表现往往难以令人满意。作者针对传统遗传算法解决高维多峰值问题时可能会出现的困难进行了分析,然后根据困难出现的原因,基于 PVM 设计了并行分布式遗传算法,并对适应度评估、交叉、变异算子做了一些改进,旨在加强算法的全局搜索能力,提高算法的收敛速度。为了验证算法多项措施的有效性,对一多峰函数在高维条件下进行多方面的测试,实验结果表明这几项措施是有效的。
并行;分布式;多峰;遗传算法
1 引言
并行计算理论的研究始于20世纪70年代,经过40多年的发展,其技术日趋成熟。在生活中有大量的实际应用,比如天气预报、地震数据处理、飞行器数值模拟等等,这些领域的事务处理往往需要几十万亿甚至几百万亿次的浮点运算,并行计算[1]是适合这类事务处理的一种技术。近年来云计算的兴起,使得分布式计算技术也逐渐趋于成熟,并得到了广泛的应用,它把网络上分散于各处的计算机资源汇聚起来完成各种大规模的计算和数据处理任务。
遗传算法(genetic algorithm,GA)基于达尔文自然选择定律以及孟德尔遗传理论,它模拟自然生物遗传和选择的过程将适应度相对高的个体保留,适应度相对低的个体逐渐淘汰,循环重复这一过程,直到满足停止条件,因此它是一种迭代搜索算法。遗传算法的全局搜索比较容易实现与加强,目前在许多领域有广泛的应用,比如建筑的结构性优化、化工领域的资源分配、计算机自动控制等等。但在高维、超高维多模态问题中,传统遗传算法仍会表现出一些不足,全局搜索能力不足,易限于局部极优,收敛速度以及精度有待提高。
文章针对传统遗传算法用于高维、超高维多模态问题时存在的不足,提出了基于PVM的并行分布式遗传算法(PVMIMGA)。PVM-IMGA算法基于PVM平台,采用了一种比较好的适应度评估方法,并对交叉算子、变异算子做了一些改进,使其具有自适应加速特性。为了验证改进工作的有效性,文章最后对一高维多峰值函数进行了实验测试,实验结果表明 PVM-IMGA算法克服了传统遗传算法易限于局部极优的问题,全局搜索能力、收敛能力都有了比较明显的提高。
2 问题分析
高维、超高维问题的一个特点是其搜索空间巨大,要在巨大的范围内搜索到合适精度的目标可行解,耗时往往较长,有时甚至无法找到。多个极值是多峰值问题的特点,多峰值问题较一般的单一峰值问题,寻优难度要更大,算法易陷于局部极值,对遗传算法的全局搜索能力会有更高的要求。
3 优化目标
在多峰值问题中,一般是寻找单类型的所有极值,即在有限定义域、可接受的时间范围内要么寻找所有极大值,要么是极小值。本文实验测试所用的多峰函数寻找的是极小值。
4 设计方案
4.1 适应度评估
多峰值问题中,各极值点的函数值往往大小不一。在传统遗传算法中,适应度的评估与位置点对应的函数值通常有比较大的关系,如果是寻找极大值,那么函数值大的,适应度值可能就比较大,而函数值小的,适应度值相对就小。这类评估方法有一定的局限性,比如当寻优目标是寻找极小值时,有些位置点的函数值较另一位置点的要大,但是它距离所在局部区域的极小值点却可能更近,因此以函数值作为参考标准的适应度评估方案显然不合适。文献[2]提出了一种基于梯度算子与聚类算子的适应度评估方法,这种适应度评估方法能够有效区分峰、谷、坡以及平原,但是它的峰、谷、坡以及平原位置点之间适应度值差距较大,坡点与谷、峰之间的接近程度难以体现,同时不利于本文的交叉变异策略,因此对它做一些改进:

由于是高维问题,因此采用浮点数编码。 表示的是位置点的偏导数,有而是用于放大临近极值点位置间差异的因子,那么的值介于0与1之间,由计算式我们知道,越是临近极值点,那么偏导数的值越是接近于0,则有反之如果是平原位置,那么的值为0,其余位置均是2,而峰、谷对应的适应度值是3,坡位置点的适应度介于2与3之间,平原位置点的适应度是 1。所以主要用于识别位置点是否处在平原。则表示m维目标问题的总适应度值。
4.2 交叉算子
在遗传算法中,交叉率体现着个体间、个体内基因交叉重组的几率。基因的交叉重组是算法实现全局搜索的重要方式,因此交叉算子的设计非常重要。文献[3]中提出了一种比较好的自适应的交叉算子,能够保证种群稳步提升,但它的选择保留策略需要不少的计算量,对于串行单机执行的遗传算法来讲,算法的搜索效率会受到一定影响。本文汲取它的一些思想并做了一些改进:个体间执行基因重组的时候,如果父亲的某个基因位点相比母亲的对应基因位点的值差异方向与该位置的偏导数符号相一致的话,那么该基因位点可以执行交叉重组。比如父亲的某个基因位置点的偏导数为正,而母亲的基因值相比父亲的要大,那么可以执行,反之不执行。执行该段基因的交叉重组之后,如果个体得到改良,则替换相应父母,继续对下一段基因做相同尝试。如果没有得到改进,采用两种策略:一种是还原该基因段,还原之后对下一段基因做相同尝试;另一种是保留这次的基因重组,继续对下一段基因做类似尝试,当父母个体全部完成基因的重组之后,得到的子代个体如果比父母要好,则做相应替换,否则不替换。这两种策略在种群进化过程中交替执行。
4.3 变异算子
遗传算法中,变异运算一般用于产生与父母性状差异小的个体,是算法执行局部搜索的主要方式。文献[3]提出的自适应变异算子同样存在计算量较多的问题,它的保留策略由于是更优则保留,否则还原,算法可能会无法进入某些区域进行搜索。为了适应PVM-IMGA算法的适应度评估方法,对变异算子进行如下设计:
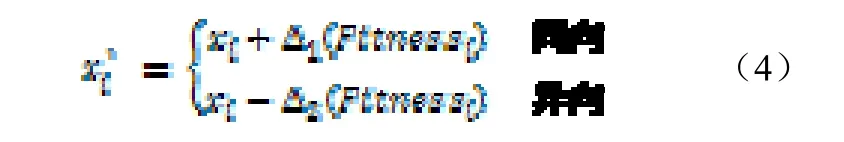
4.4 优化辅助策略
在遗传算法中,初始种群的特征也是影响算法搜索效率的一个因素。在多峰值问题中,许多极值点往往是分布在不同的空间区域,所以一般来讲,应该让初始种群中的个体尽量分散,这样更有利于算法将个体收敛到它附近的极值。
种群规模过大或者过小,都不利于算法的执行。当算法将个体收敛到指定精度后,我们可以迁徙该个体,并将一些距离该个体一定欧氏距离之外个体补充到进化的种群中,保持种群的多样性,避免算法陷于局部极优区域。
如果目标问题具有约束处理条件,那么问题的寻优难度会增大。文献[3]中提出了一种比较好的约束处理方法,为了更好的利用伪可行解的进化信息,PVM-IMGA算法也采用类似的约束处理策略。
4.5 并行分布式计算方案
PVM-IMGA算法基于消息传递类并行软件开发环境PVM[4],采用的是Master-Slave模式(MPMD),这种模式的程序是由运行于一台PVM主机上的Master PVM程序和运行于若干计算节点的Slave PVM程序组成的。Master主机负责计算任务的管理调度以及数据收集分配,Slave计算节点负责算法的计算搜索任务。
网络上的数据通信开销是比较大的,因此应尽量减少网络通信,缩短算法运行时间。为了做到这一点,坚持本地化数据处理,即从主机下发给计算节点Slave的是搜索空间的范围,计算节点再根据规则本地化生成个体对象,每个计算节点完成搜索任务后,反馈回主机的也是决策变量的值,主机再根据决策变量得出相关信息。
PVM-IMGA算法的一个完整的执行过程是这样的:Master主机将待处理的大数据划分为很多数据块,在算法中,我们按照一定规则划分决策变量的范围,使搜索空间成为细块。主机将一个个的数据块下发到网络上的可用计算节点,然后等待节点返回搜索结果,收集完成后继续分配未处理的数据块,直到所有数据块完成分配和搜索计算,汇总所有的计算结果作为最终结果。
5 算法流程
PVM-IMGA算法的执行流程如下:
(1)参数设置:包括并行分布式环境的建立,数据块划分数目,计算节点上种群的规模,算法迭代停止条件等等。
(2)任务分配:Master主机给Slave计算节点下发搜索空间数据以及其他信息,比如算法迭代次数、小生境半径等等。
(3)计算节点环境初始化:计算节点根据从主机发送来的参数信息,初始化进化种群。
(4)基因的交叉重组、变异:每一个计算节点独立完成各自的搜索任务。当算法达到迭代停止条件时,将搜索到的有用信息传回Master主机。
(5)数据的收集以及任务再分配:Master主机负责从计算节点收集信息,如果仍有数据搜索任务未分配,则将任务下发给该可用计算节点,然后等待其他节点的数据。
(6)判断:如果主机之上仍有未分配的搜索任务或者计算节点上有未传回的信息,那么重复第 5步骤,否则停止整个算法的运行,汇总所有搜索到的有用信息。
6 实验测试
Keane’s Bump 函数

这是一个国际上广泛用于测试算法稳定性、收敛性能的多峰值函数,在超高维的条件下,它具有超非线性、超多峰的特征,函数维度越高,搜索难度越大。
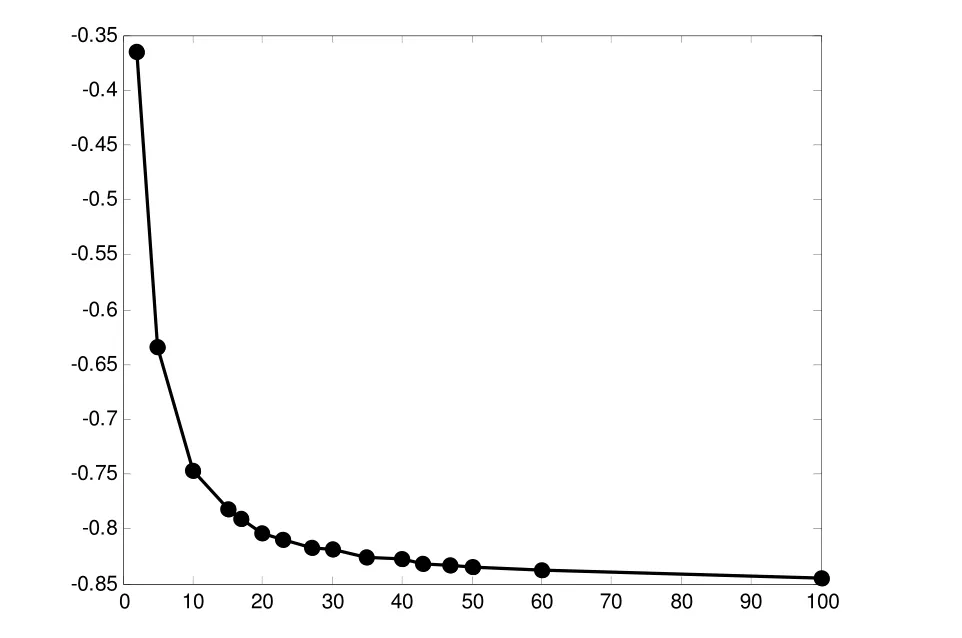
图1 Keane’s Bump 函数的最小值与维度的关系
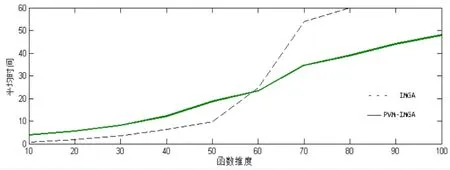
图2 不同维度下PVM-IMGA与IMGA的平均搜索时间
为了检验论文提出的并行分布计算方式的有效性,笔者将论文改进后的遗传算法分别在 PVM并行环境以及单机环境对Keane’s Bump 函数进行实验测试20次,然后求它们的平均时间。两种算法的实验条件相同,例如相同的种群规模、迭代次数等等。图2是在不同维度下,使用PVM-IMGA算法以及单机环境下的IMGA算法的平均搜索时间变化趋势图。从图我们可以看到,在较低维度的条件下,单机环境下的IMGA算法的搜索时间要比并行环境下的PVM-IMGA算法的执行时间要短,但是当维度逐渐增高之后,它们的搜索时间的差距有了一些变化,当维度高到一定程度时,PVM-IMGA算法的执行效率要比单机环境的IMGA算法要高。另外,当维度达到一定高度后,IMGA算法无法在指定的迭代次数内找到所有极值,当增加种群规模以及迭代次数时,其搜索结果会有一点变化,但是仍然是无法达到多峰值问题的寻优要求。之所以出现这样的结果,究其原因,当维度比较低,问题的搜索空间不是很大时,IMGA具有较好的求解能力,可以比较快速的找到可行解,PVM-IMGA算法虽然也具有求解能力,但是因为网络传输需要比较长的时间,所以PVM-IMGA算法的耗时比IMGA算法要长。但是当维度较高,搜索空间比较巨大时,IMGA算法的局限性就暴露出来了。而PVM-IMGA算法因为能将搜索空间分块细化,并交由不同的计算节点来执行,执行效率开始变得更高。当问题维度增大到一定程度时,笔者可以通过调整数据块大小以及增加计算节点来提高算法的搜索效率。

表1 50维条件下的测试对比
为进一步验证PVM-IMGA算法的稳定性以及收敛能力,笔者对算法能收敛到的最小极值进行统计,并与文献[5]的DE、ABC、HABC算法,文献[3]的IMBF-GA算法进行比较。从表1的 4项实验数据可见,在收敛能力和稳定性方面,PVM-IMGA算法皆优于DE、ABC、HABC、IMBF-GA算法,说明PVM-IMGA算法在高维条件下,对多峰函数具有较好的收敛能力,文章针对多模态问题,对传统遗传算法进行的多项修改是有效的。
文献[3]中提到IMBF-GA算法在一定维度下,搜索到所有极值的概率是比较高的,但是当维度增加时,成功率会下降。对于本文的 PVM-IMGA算法,如果去除并行分布式计算形式,仅使用单机运行,其运行效果与IMBF-GA算法大致类似,增大种群规模以及迭代搜索次数尽管能在一定程度上提高成功率,但是当函数维度达到一定程度后,算法执行效率、收敛效果仍然难以让人满意。并行分布式计算方式是解决超大规模计算的有效手段,这也是当今云计算与分布式系统流行的一个重要原因。
[1] Kai Hwang.云计算与分布式系统:从并行处理到物联网[M].北京:机械工业出版社,2013.
[2] 刘洪杰,王秀峰.峰搜索的自适应遗传算法[J].控制理论与应用,2004,4(21): 303-310.
[3] 黄春.改进遗传算法的函数优化及应用[D].南宁:广西大学, 2015.
[4] Adam.Parallel Virtual Machine:A Users' Guide and Tutorial for Networked Parallel Computing[M].The MIT Press,1994.
[5] 林志毅,王玲玲.求解高维函数优化问题的混合蜂群算法[J].计算机科学,2013,3(40): 279-281.
The research of parallel and distributed genetic algorithm
In the face of complex problems with a large number of search spaces, traditional genetic algorithm’s performance is often difficult to satisfactory. The author analyzes those possible difficulties for solving high-dimensional multimodal problems by traditional genetic algorithm. Then according to the cause that difficulties occur, we design parallel and distributed genetic algorithm based on PVM, and make some improvements to the evaluation method of fitness, the crossover and mutation operator. These improvements aim at strengthening the global search ability and improving the rate of convergence of the algorithm. In order to verify the measures’ effectiveness of the algorithm, we take a test to a multi-modal functions in many aspects under the condition of high dimension. The experimental results show that the several measures are effective.
Parallel; distributed; multi-modal; GA
TP302
A
1008-1151(2016)07-0013-03
2016-06-11
何文静(1987-),女,广西大学计算机与电子信息学院硕士生,研究方向为并行分布式计算和优化算法。
