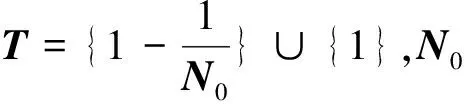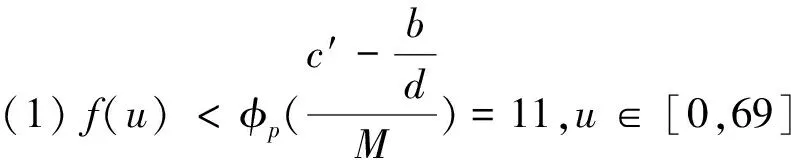时间尺度上三阶非线性p-Laplacian边值问题三个正解的存在性
2016-12-02王颖
王 颖
(安徽科技学院 信息与网络工程学院 数学系,安徽 滁州 233100)
时间尺度上三阶非线性p-Laplacian边值问题三个正解的存在性
王 颖
(安徽科技学院 信息与网络工程学院 数学系,安徽 滁州 233100)
研究了时标上一个新的三阶非线性p-Laplacian 三点边值问题,利用广义Leggett-Williams不动点定理得出该边值问题至少有三个正解存在的结论,并给出相应的例子,其结果推广了已有的研究.
时间尺度;p-Laplacian;边值问题;不动点定理
1900年Stefan Hilger 发表了时间标度分析[1],这一理论在连续与离散之间建立了一座桥梁,使人们可以同时处理连续系统和离散系统,并且有重要的应用价值.这一新兴课题引起数学家们的广泛关注,许多学者都投入到时标上微分方程的研究特别是边值问题正解的研究中来,如文献[2-8]及其参考文献.随着时标理论自身的迅速发展和不断完善,如何利用非线性泛函分析中先进的分析工具来研究时标上含p-Laplacian的边值问题解的存在性引起许多数学工作者的浓厚兴趣,见[9-15]及其参考文献.其中大部分研究的都是二阶含p-Laplacian的边值问题,三阶及以上的方程研究的少一些,因此还有许多问题可以深入研究.
在[14]中何智敏等人研究了时标上二阶p-Laplacian边值问题
[φp(u△(t))]▽+g(t)f(u(t))=0,t∈(0,T),
u(0)-B0(u△(0))=0,u△(0)=0或u△(0)=0,u(T)+B1(u△(T))=0,
得出至少有三个正解存在的准则.
[15]中,Hu等人研究了时标上三阶三点边值问题
[u△△(t)]▽+ω(t)f(t,u(t))=0,t∈[a,b],
u(ρ(a))-βu△(ρ(a))=αu(η),γ(u(η))=u(b),u△△(ρ(a))=0.
该文利用锥压缩拉伸不动点定理得到上述边值问题正解的存在性的若干判定准则.
受上述研究的启发,本文研究了时标上三阶非线性p-Laplacian三点边值问题
[φp(a(t)u△▽(t))]▽+ω(t),f(t,u(t))=0,t∈(0,T)∈T,
(1)
βu(0)-γu△(0)=b,u△(T)=αu(η),u△▽(0)=0,
(2)

假设以下条件在文中始终成立:
(H1) f(t,u(t)):[0,T]×R→R+是连续的;
(H2) a(t)∈C([0,T],(0,+∞))为单调递增函数;
(H3) ω(t):[0,T]→[0,+∞)是ld-连续的,且ω(t)在[0,T]上的任意子集上不恒为零.
1 预备知识
关于时间尺度的一些基本定义和定理可见Atici,Guseinov[16]及Bohner,Peterson[17],本节只给出主要结论要用到的常见引理和不动点定理.
引理1 如d≠0,h(t)∈Cld(T,R)则动力方程边值问题
[φp(a(t)u△▽(t))]▽+h(t)=0,t∈(0,T),
(3)
βu(0)-γu△(0)=b,u△(T)=αu(η),u△▽(0)=0,
(4)
有唯一解


(5)

(6)

(7)
令t=T,η代入式(6)(7)有

(8)

(9)
将(8),(9)式代入(4)式,有


将上式代入式(7)可得式(5).证毕.







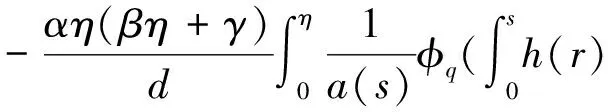
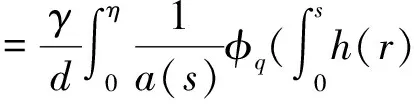


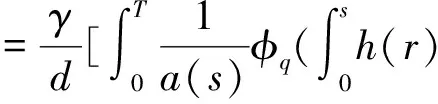

证毕.

P={u∈E|u在[0,T]中是凹的,递增且非负}.
设γ是定义在实Banach空间中的锥P的非负连续函数,对任一的c>0,集合
P(γ,c)={u∈P|γ(u) γ(x)≤β(x)≤α(x)且‖x‖≤Mγ(x). 假设存在全连续算子T:P(γ,c)→P及正数a,b,0 (i)γ(Tx) (iii)P(α,a)≠⟩,α(Tx) 0≤α(x1) 定义算子A:P→E使 (10) 易知边值问题(1)(2)有解u(t)当且仅当u是算子方程(10)的不动点. 给定一内点l∈T,且η 则边值问题(1)(2)至少有三个正解u1(t),u2(t),u3(t)满足 0<φ(u1) 引理4中的条件(i)成立. 接着证明引理4中的条件(ii)成立.选取u∈∂P(θ,b′),则 由(H5),当t∈[η,T]有 从而引理4中的条件(ii)成立. 最后验证引理4中的条件(iii)成立.当t∈[0,T]时,有 据条件(H6)可得,当t∈[0,T]时有 则引理4的条件(iii)成立. 0≤φ(u1) 即边值问题(1)(2)至少存在三个正解.证毕. [φp(a(t)u△▽(t)]▽+ω(t)f(t,u(t))=0,t∈(0,1), (11) βu(0)-γu△(0)=b,u△(T)=αu(η),u△▽(0)=0, (12) 据定理1,边值问题(11),(12)至少存在三个正解u1(t),u2(t),u3(t)满足 [1] HILGER S. Analysis on measure chains-a unified approach to continuous and discrete calculus[J]. Results Math, 1990,(18):18-56. [2] KAUFMANN E R. Positive solutions of a three-point boundary value problem on a time scale[J]. Electron J Differ Eqs, 2003,2003:1-11. [3] ANDERSON D R, AVERY R I. An even order three-point boundary value problem on time scales[J]. J Math Anal Appl, 2004,291:514-525. [4] SUN H R, LI W T. Positive solutions for nonlinear three-point boundary value problems on time scales[J]. J Math Anal Appl, 2004,299:508-524. [5] FENG M, ZHANG X, GE W. Positive solutions for a class of boundary value problems on time scales[J]. Comput and Math with Appl, 2007,54:467-475. [6] ANDERSON D R. Solutions to second order three-point problems on time scales[J]. J Diff Eqs and Applications, 2002,8:673-688. [7] LI W T, SUN H R. Multiple positive solutions for nonlinear dynamical systems on a measure chain[J]. J Comput Appl Math, 2004,162:421-430. [8] AGARWAL R P, REGAN D. Existence of positive solutions to time scales equation using time scales inequalities[J]. J Differ Equation Appl, 2001,7:829-836. [9] SONG C, WENG P. Multiple positive solutions for p-Laplacian functional dynamic equations on time scales[J]. Nonlinear Analysis: Theory, Methods & Applications, 2008,68(1):208-215. [10] SUN H R, LI W T. Existence theory for positive solutions to one-dimensional p-Laplacian boundary value problems on time scales[J]. J Differ Eqs, 2007,240(2):217-248. [11] HE Z, JIANG X. Triple solutions of boundary value problems for p-Laplacian dynamic equation on time scales[J]. J Math Analysis an Appl, 2006,321(2):911-920. [12] ZHOU C, MA D. Existence and itetation of positive solutions for a generalized right-focal boundary value problems with p-Laplacian operator[J]. J Math Analysis an Appl, 2006,324(1):409-424. [13] XU F Y. Positive solutions for third-order nonlinear p-Laplacian m-point boundary value problems on time scales[J]. Discrete Dynamics in Nature and Society, 2008,2008:16 pages. [14] HE Z M, LI L. Multiple positive solutions for the one-dimensional p-Laplacian dynamic equation on time scales[J]. Math Comput Modelling, 2007,45(1-2):68-79. [15] HU L G. Positive solutions to singular third-order three-point boundary value problems on time scales[J]. Math Comput Modelling, 2010,51(5-6):606-615. [16] BOHNER M, PETERSON A. Dynamic equations on time scales: an introduction with applications[M]. MA: Birkhauser Boston,2001. [17] ATICI F M, GUSEINOV G S. On Green's functions and positive solutions for boundary value problems on time scales[J]. J Comput Appl Math, 2002,141:75-99. [18] HE Z M. Double positive solutions of three-point boundary value problems for p-Laplacian dynamic equation on time scales[J]. J Comput Appl Math, 2005,182:304-315. [19] REN J L, GE W G, LI C Z. A theorem of triple positive solutions for multi-point boundary value problems[J]. Ann of Diff Eqs, 2003,19(4):540-546. The Existence of Triple Positive Solutions for Third-Order Nonlinear p-Laplacian Boundary Value Problems on Time Scales WANG Ying (Department of Mathematics of College of Information and Network Engineering, University of Science and Technology, Chuzhou 233100, China) A new third-order nonlinear p-Laplacian three-point boundary value problem on time scales is studied. By the Generalized Leggett-Williams fixed point theorem in cones, a new result of at least three positive solutions of the boundary value problem is obtained. As an application, an example is given to demonstrate the main result. The result generalized the past research. time scales; p-Laplacian; boundary value problem; fixed point theorem 2015-09-23 安徽省高校自然科学研究重点项目(KJ2016A174);安徽科技学院自然科学研究一般项目(ZRC2014441). 王颖(1975-),女,江苏徐州人,副教授,硕士,研究方向为泛函微分方程. 10.14182/J.cnki.1001-2443.2016.05.002 O175.8 A 1001-2443(2016)05-0414-06

2 主要结果



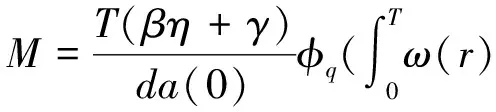




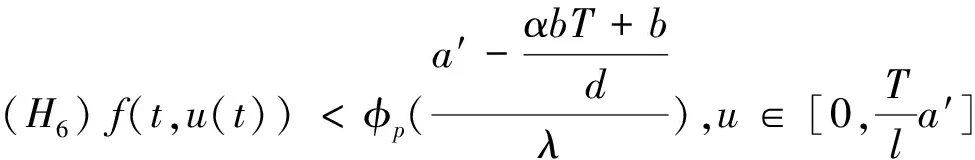
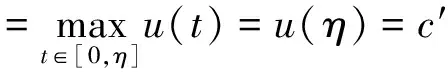


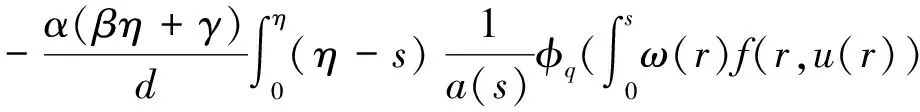

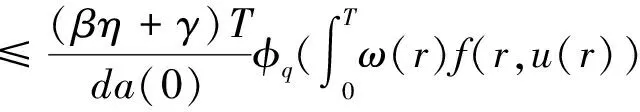


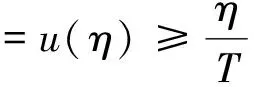




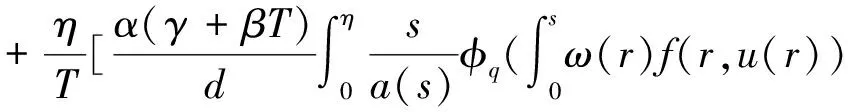



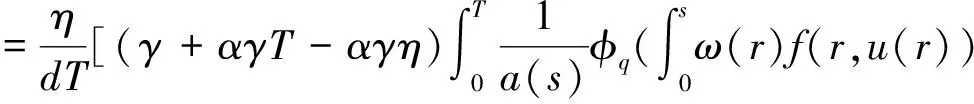
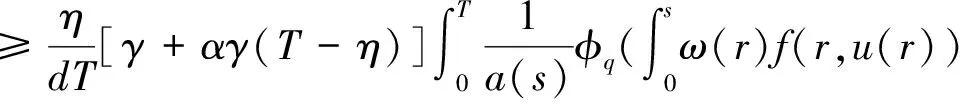
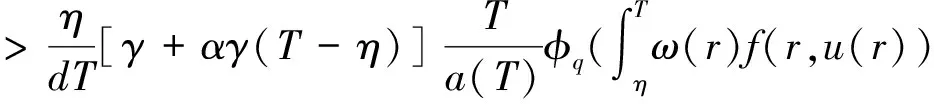



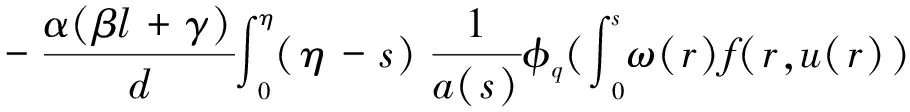


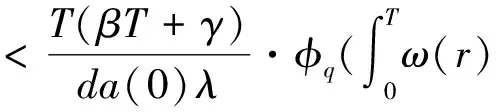
3 应用举例