基于点到曲面投影的飞机蒙皮波纹度计算方法

张 俐， 吴中林

(北京航空航天大学机械工程及自动化学院，北京 100191)

基于点到曲面投影的飞机蒙皮波纹度计算方法

张 俐， 吴中林

(北京航空航天大学机械工程及自动化学院，北京 100191)

为了精确检测飞机蒙皮表面的波纹度，提高检测效率，研究了一种改进的点到参数曲面投影算法，即使用椭圆环面片逼近蒙皮设计曲面的方法求解点到曲面的投影，采用该方法从曲面的测量点云中提取待测波纹度位置的测量点，并计算测量点与理论位置的偏差值。根据偏差值的大小变化趋势提取局部极值即波峰波谷值，并计算相应的波长，结合波纹度的定义完成波纹度计算。实验结果表明，该方法分析结果准确、效率高。

波纹度；点到曲面投影；局部极值；飞机蒙皮

飞机蒙皮表面的波纹度会对飞机气动特性和飞行性能造成较大影响[1]。在飞机的研制、试飞取证以及量产过程中都需要对飞机蒙皮表面的波纹度进行检测。因此，在飞机外形容差规范中，对波纹度有严格规定。

目前，由于用实物样条方法检验波纹度的精度和效率低等原因，各飞机制造商基本已经放弃该方法，但是尚未有其他规范成熟的测量工具来精确分析波纹度[1]。随着三维测量技术的发展，为通过软件来精确分析飞机表面波纹度提供了可能性。

1 波纹度分析方法的思路

波纹度是用来描述介于零件表面粗糙度和形状误差之间的物体表面轮廓不规则变化[2]。工程中常用波幅和斜率来定量表示波纹度，如图1所示。通常将相邻两波峰的距离称为波长，用L表示；波

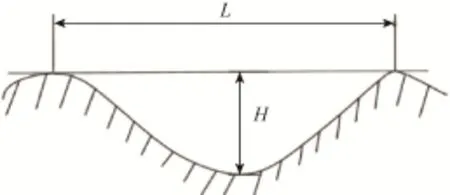
图1 波纹度的定义

传统的波纹度检测方法主要有3种：钢尺法、卡板法和特征样条法。随着三维数字化测量技术在航空工业领域的普及，波纹度的检测方法有了很大改进。马明等[2]提出应用小波滤波技术分析飞机蒙皮表面的波纹度。金鼎和吴剑[1]借助Max/Exa-scan测量系统采集飞机表面信息，结合 CATIA软件对三维数字采集数据进行分析，最终获得被测区域波纹度情况。于立明和李启明[3]利用最小二乘拟合方法获取曲面、曲线的波纹度数据。

本文波纹度计算是在传统的波纹度检测方法基础上，结合三维数字化测量技术，改进点到参数曲面的投影算法来提取测量点并使用新的方法计算波纹度。

1.1 基准曲线的确定

波纹度反映的是曲线波动情况，目前波纹度检验通常采用的是将被测外形面按横向或纵向划分百分线的模拟量测量方法。因此，以此为依据，在理论曲面上确定一条基准曲线，即百分线。并通过比较测量点与基准曲线的偏差波动来分析计算波纹度。

已知飞机蒙皮理论参数曲面表达式为 S(u,v)，其中 u，v为曲面的两个参数。基准曲线是按如下方法确定的：

(1) 若给定理论曲面纵向波纹度检测的百分比K，即在曲面两条横向边界曲线上确定两点P0、P1，使得P0、P1点到两条横向边界曲线开始位置的弧长分别占各自边界曲线总弧长的百分比为K。如图2所示，；若给定横向波纹度检测百分比，则位置点P0、P1位置也按照上述方法确定。

(2) 将连接P0、P1点的直线投影到理论曲面上，如图3所示，投影曲线Lp即为基准曲线。

图2 P0、P1为纵向百分比K确定的两个边界点

图3 Lp为基准曲线

1.2 实现流程

如图3所示，将曲面上连接点P0、P1点的直线离散化为等间距的有限个点，将这些点投影到理论曲面上求得投影点，根据投影点能够生成基准曲线Lp。已知基准曲线上的点，结合文献[4]中有关方法，提取测量点并计算测量点偏差值。最后根据偏差值计算波长及波峰波谷值，完成波纹度计算。整个算法的流程图如图4所示。

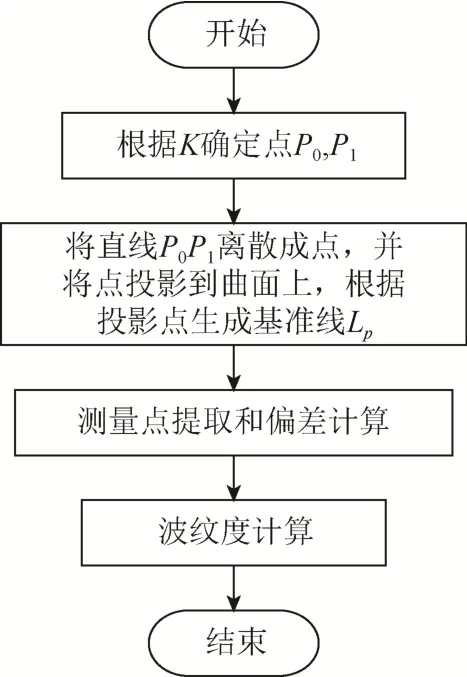
图4 波纹度计算流程

2 测量点的提取和偏差计算

根据直线P0P1参数方程，按一定的步长取直线上的点，其中，。再用分割逼近法[5]计算测量点 P0到理论曲面的最短距离的点 Q′(u′,v′)。以 Q′(u′,v′)为初始

在求得当前投影点T0和参数(u0,v0)以后，下一个投影点计算的初始值是当前投影点，以此类推计算点iP′在曲面上的投影点Ti和参数(ui,vi)，直到i=N。

2.1 点到曲面的投影计算

计算点到参数曲面投影的方法主要有两大类：迭代法和细分法。迭代法又分为代数求根法和几何迭代法。代数求根法的代表算法是Mortenson[6]提取的一种数值计算法以及Piegl和Tiller[7]提出的方法。几何迭代法有Hu和Wallner[8]提出一种二阶几何迭代法；Liu等[9]提出的圆环面片逼近法。Piegl和Tiller[10]、Ma和Hewitt[11]、Selimovic[12]都提出了细分曲面的无效曲面片排除准则。

代数求根法对初始迭代点要求高，而细分法计算复杂。在几何迭代法中Liu等[9]的方法计算效率相对较高，但是稳定性有待进一步提高。所以本文对Liu等[9]的方法进行改进，用椭圆环代替圆环逼近曲面，计算效率和稳定性都有提高。

2.1.1 椭圆环面片逼近法求投影点

如果将笛卡尔坐标原点放在椭圆环面中心，则椭圆环的方程式为

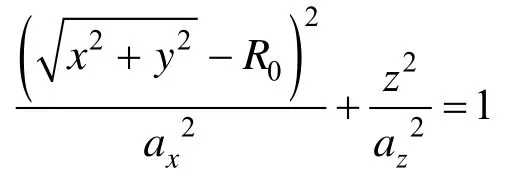
其中，R0为环的大半径；ax和az为椭圆环横截面椭圆的长、短半径，如图5所示。

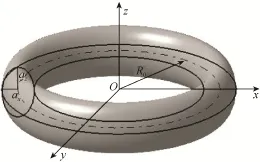
图5 坐标原点在椭圆环中心的示意图

已知参数曲面S(u,v)，给定其参数域内的一个参数(u0,v0)，计算该参数对应的点 Q=S(u0,v0)、曲面在该点的单位法向量n、两个主曲率k1，k2和对应的单位主方向e1，e2。

首先要对上述几何信息进行预处理，具体如下：

(2) 如果k1＞0，将n、k1和k2都乘以–1，改变其符号。这样的预处理保证和k1≤0。

然后构造这样的椭圆环面S′：中心在Q+n/k1，轴向为e2。椭圆的短轴，长轴。当k2＜0时，中心圆的半径为；当k2＞ 0时，中心圆的半径为。椭圆环面S′和原曲面S在点Q处有相同的法向、主曲率和主方向。根据前面所做的预处理，这个椭圆环面是唯一确定的。在本文的逼近方法中，采用椭圆环的局部面片来逼近曲面。

在构建原曲面的逼近椭圆环面以后，将测试点T投影到椭圆环面片上，求得投影点T′，然后求T′在原曲面上的参数。对于上述的椭圆环面片，求点到其投影可分为以下两步：

(1) 将测试点T投影到中心圆上，求得横截面椭圆的位置。

(2) 将测试点T投影到横截面椭圆上，求得投影点T′。

在上述第二步中，测试点和横截面椭圆在同一平面上。求点到平面椭圆的投影时，建立一个关于未知数为θ的一元四次方程。由于测试点和椭圆位于一个平面上，所以方程一定有实数解，而且有两个解，其中到测试点最近的点作为投影点T′。

分别用本文介绍的椭圆环逼近求点到曲面方法和文献[9]中的圆环逼近法测试文献[8]中的实例1，算法的收敛准则都采用Piegl和Tiller[7]的标准，即

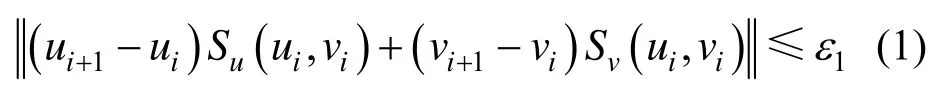
本文中当 ε1≤ 10-10时，迭代终止。表1列出了当测试点为(120, 10, 100)，初始参数值为(0.9, 0.6)时，每次迭代的参数增量Δu、Δv和迭代次数。表2中列出了初始参数值为(0.4, 0.1)时的情况。

表1 测试点(120, 10, 100)初始值(0.9, 0.6)的迭代次数和参数增量表

表2 测试点(120, 10, 100)初始值(0.4, 0.1)的迭代次数和参数增量表

由表1可以看出，本文采用的椭圆环逼近法只需要迭代 4次就能达到迭代终止条件，而文献[9]中使用的圆环面片逼近法则需要迭代5次。表2中，在初值参数值与真实参数值的差值较大情况下，本文的方法也能比文献[9]使用的方法少迭代1次，迭代效率分别提高25%和14%。

2.1.2 基准曲线上点的求取

将通过使用分割曲面法[5]求得的点Q0(u′,v′)作为初始迭代点，在该点构造椭圆环面片，并将起始点投影到椭圆环面片上，求得点，再用Newton迭代法求点在曲面S上对应的参数(u1,v1)和坐标值T1。算法框架如下：

(1) 计算曲面在初始迭代点处的几何信息，包括位置Q0，法向量n，两个主曲率k1，k2和相应的主方向e1，e2。

(2) 应用这些几何信息，在Q0处构造一个椭圆环面片ST。

(4) 用这个新的参数作为初值，重复步骤(1)～(3)，直到求得的参数满足必要的精度。图6是以Q0初始迭代点，点在椭圆环面上的投影点。

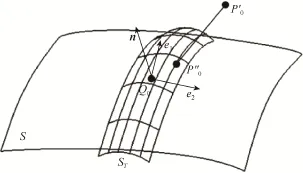
图6 点在椭圆环面上的投影

2.2 测量点的提取和偏差计算

根据求得的投影点Ti以及对应的曲面参数(ui,vi)，其中 i= 0,1,… ,N ，计算曲面S在点Ti处的法向量 ni(ui,vi)。在测量点云中搜索到法向量ni距离最近的测量点，并记最短距离为di，若di小于给定的阈值则提取该测量点并计算测量点到 Ti点的距离在法向的投影值Di，把该值作为了测量点到曲面的偏差；否则排除，如图7所示。

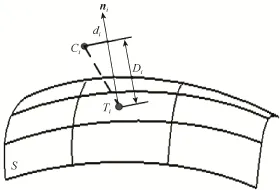
图7 根据曲面上点Ti提取测量点Ci并计算偏差Di

3 波纹度计算

由于文献[1-3]所述方法的不足，本文使用一种新的波纹度计算方法，即在完成测量点的提取以及每个测量点的偏差计算后，通过依次比较偏差值大小的方法来分析波纹度。

根据波纹度的定义，波峰、波谷为测量点到曲面距离的局部极值，即测量点偏差的局部极值；波长为相邻波峰(或波谷)对应基准曲线的弧长。

记得在纪录片也看到过这样的故事，冰岛国家破产，金融危机阶段，许多人去了邻国挪威找工作，然而过了些年，大家又回来，引起了冰岛当地媒体的好奇，接受采访，有人说是对冰岛经济又有了信心，克朗贬值，旅游业大力发展，也有一群人的答案整齐统一：为了暖气！挪威烧煤供暖，费用惊人，难怪家家户户有古老的壁炉，宁可烧木柴，缺点是只有客厅热，要是卧室睡觉，或厕所洗澡，冷得哭出声。

在计算波纹度之前，先对测量点的偏差Di进行如下预处理：

(1) 将测量点的偏差按照之前计算顺序依次进行前后比较，后者较大的值用1表示，否则以–1表示。将比较的结果存入数组COMP中。

(2) 依次统计数组COMP中每个1、–1的连续个数，结果保存到数组LinkNum中，并将每个连续的开始点在测量点中对应位置存在数组Index中。

波峰、波谷值提取方法流程图如图8所示。

已知测量点偏差值和基准曲线上的点 Ti是一一对应的关系，根据偏差值的极值就能确定极值在Ti中对应点。相邻波峰(或波谷)对应Ti中两点之间距离即为波长。

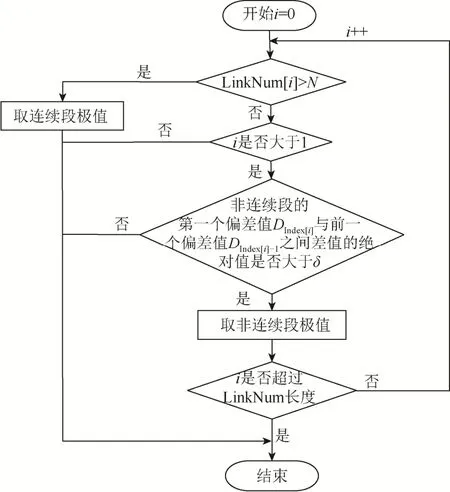
图8 波峰、波谷值提取方法流程图

4 实例验证

根据上述方法开发波纹度检测程序，用机翼上蒙皮进行波纹度检测验证。图9给出了翼面各百分比位置的波纹度检测实例。

理论曲面如图9(a)所示。对原始测量点云进行去噪、简化等预处理，并导入程序中，显示结果如图9(b)所示。然后对点云进行坐标变换，提取纵向62%位置的测量点，如图9(c)所示。测量点的偏差曲线如图9(d)所示，其中测量点横坐标为该点在基准曲线Lp的弧长位置，纵坐标为偏差值。计算的波纹度值如图9(e)，其中每一个矩形框代表一个波纹度值，矩形框的纵坐标为波纹度值，矩形框的长度为波长，矩形框在横坐标中的位置为波长在基准曲线弧长中的位置，检测波纹度的标准参考文献[13]。

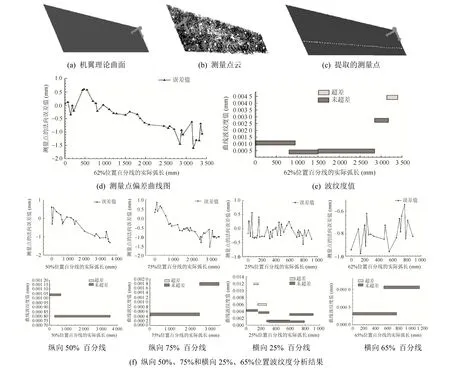
图9 实验过程

对比图9(d)和(e)，图9(e)中波纹度的分布情况符合其曲线波幅分布情况。在图9(f)中，分别对纵向50%、75%和横向25%、65%位置进行波纹度计算结果。通过图9的实验验证，本文能快速、有效地分析曲面的波纹度，分析效率高。

5 结束语

本文在总结传统波纹度检测经验基础上，结合先进的数字化检测设备，使用投影算法和波峰、波谷提取方法分析波纹度。该方法通过实验验证，并实际运用于飞机蒙皮波纹度检测。

从2.1节的实验数据可以看出，同一测试点，在迭代效率上，本文使用椭圆环面片逼近法求点到参数曲面的投影方法，比文献[9]圆环面片逼近法求投影的方法迭代效率分别提高25%和14%。

通过使用新的波纹度分析方法，能够实现波纹度的快速分析计算，不依赖测量仪器，也不需要人工提取波峰、波谷点。只需要给定整个曲面的测量点，就可以实现曲面各个位置波纹度的检测。本文的方法比金鼎使用的方法更自动化。

需要指出的是，由于测量点的疏密直接影响波纹度计算的结果，所以为保证波纹度分析的准确性，在保证计算速度的前提下应提高测量点的密度。

[1] 金 鼎, 吴 剑. 基于三维测量技术的飞机表面波纹度数字化分析方法[J]. 航空工程进展, 2013, 4(1): 85-89.

[2] 马 明, 曹喜锋, 李启明, 等. 基于小波滤波的民用飞机蒙皮表面波纹度分析方法[J]. 科学技术与工程, 2013, 13(35): 10750-10754.

[3] 于立明, 李启明. 基于最小二乘法的飞机蒙皮波纹度处理方法研究[J]. 科技信息, 2012, (28): 424-427.

[4] 刘子路, 张 俐, 郑国磊. 一种基于CAD的翼类曲面误差检测方法[J]. 图学学报, 2012, 33(6): 136-139.

[5] 廖 平. 基于遗传算法和分割逼近法精确计算复杂曲面轮廓度误差[J]. 机械工程学报, 2010, 46(10): 1-7.

[6] Mortenson M. Geometric modeling [M]. New York: John Wiley & Sons, 1985: 505-525.

[7] Piegl L, Tiller W. The NURBS book [M]. 2nd ed. New York: Springer, 1997: 232-234.

[8] Hu S M, Wallner J. A second order algorithm for orthogonal projection onto curves and surfaces [J]. Computer Aided Geometric Design, 2005, 22(3): 251-260.

[9] Liu X M, Yang L, Yong J H, et al. A torus patch approximation approach for point projection on surfaces [J]. Computer Aided Geometric Design, 2009, 26(5): 593-598.

[10] Piegl L A, Tiller W. Parametrization for surface fitting in reverse engineering [J]. Computer-Aided Design, 2001, 33(8): 593-603.

[11] Ma Y L, Hewitt W T. Point inversion and projection for NURBS curve and surface: control polygon approach [J]. Computer Aided Geometric Design, 2003, 20(2): 79-99.

[12] Selimovic I. Improved algorithms for the projection of points on NURBS curves and surfaces [J]. Computer Aided Geometric Design, 2006, 23(5): 439-445.

[13] 何文治. 航空制造工程手册:飞机装配[M]. 北京: 航空工业出版社, 2010: 14-15.

A Calculation Method of Aircraft Surface Waviness Based on the Method of Point Projection on Curved Surface

Zhang Li, Wu Zhonglin

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

To measure the waviness of aircraft surface accurately and efficiently, an improved algorithm for the projection of points on parameter-curved surface is proposed. The point projection on curved surfaces is calculated by adopting the approach of elliptical torus patch approximation. Firstly, by using this algorithm, points are extracted from the surface’s massive measuring points and the offset value between measuring points and their projection on the theoretical positions is calculated. Secondly, the local extremum is extracted at the peak and valley of waviness according to the variation trend of the offset value. Then its corresponding wavelength is calculated. Finally, the waviness is calculated based on its definition. Experiments show that this method is highly efficient, and generates accurate results.

waviness; point projection on surfaces; local extremum; aircraft surface

TP 391

10.11996/JG.j.2095-302X.2016050626

A

2095-302X(2016)05-0626-06

2015-12-23；定稿日期：2016-03-19

基于工艺驱动的全机全三维综合测量系统开发与集成技术项目(2013E11222)；飞机后段自动精准对合技术与成套设备项目(2014ZX04001-081-07)

张 俐(1961–)，女，北京人，高级工程师，学士。主要研究方向为飞机数字化装配检测技术。E-mail：gracejune@buaa.edu.cn