五轴后置处理转角选解优化及奇异区域处理方法的研究

余 丹， 闫光荣， 范庆香， 丁 涛， 徐翔宇

(北京航空航天大学机械工程及自动化学院，北京 100191)

五轴后置处理转角选解优化及奇异区域处理方法的研究

余 丹， 闫光荣， 范庆香， 丁 涛， 徐翔宇

(北京航空航天大学机械工程及自动化学院，北京 100191)

五轴后置处理是将CAM软件系统产生的刀位文件转换成数控机床加工程序的关键环节。基于五轴后置处理过程中转角选解、优化以及奇异区域加工数据处理的问题，提出了一种集合转角选解、优化及奇异区域处理的方法，解决了因后置处理中选解不当引起的碰撞、旋转轴在相邻刀位之间摆幅过大以及在奇异区域旋转轴产生急速转动、非线性误差过大等问题。该方法应用C++语言开发了相应的后置处理系统，通过读取CATIA刀位文件，生成可执行数控加工程序，经Vericut仿真验证该算法可行。

五轴数控加工；后置处理；选解优化；奇异区域处理

五轴联动数控加工对于航空航天、汽车以及模具领域复杂且具有高精度加工要求的零件加工的应用越来越广泛。五轴联动数控机床因其两个旋转轴的参与，手工编制数控加工程序费时费力，并且难以保证正确性，因而开发相应的后置处理器尤为重要。

后置处理是将 CAM系统生成的刀位文件转换成相应数控机床/数控系统的数控加工程序。五轴数控加工刀位文件在后置处理过程中，考虑到实际五轴数控加工中可能出现的问题，例如因后置处理中选解不当引起的碰撞、旋转轴在相邻刀位之间摆幅过大以及在奇异区域旋转轴产生急速转动、非线性误差过大等，需要对求解得到的坐标数据进行一系列的优化处理。

Affouard等[1]提出采用修正刀具轨迹的方法使刀具避开奇异区域，但是算法复杂，计算代价较大。Sørby[2]提出了一种在奇异点附近线性插值的算法，同时修改 C轴转角，避免加工通过奇异点时误差过大，但通过此方法获得插值会使得 C轴转动速度发生突变，给机床带来较大的冲击。杜娟等[3]针对复杂曲面环形刀五轴数控加工中的局部干涉问题，提出了一种基于曲率匹配及网格点的干涉处理技术。She等[4-6]提出了一种基于雅可比矩阵的奇异区域检测与处理算法，并针对奇异区域刀位点进行 C角优化，并对不满足非线性误差要求的插值刀位点进行递归线性插值处理，但对于非线性误差较大的奇异区域，其递归的层次较高，计算复杂。本文在相关研究的基础上，对五轴数控加工后置处理过程中转角选解及优化问题进行了系统的研究，提出了一种较为系统、简便的转角选解及奇异区域优化处理方法。

1 算法研究

1.1 机床运动学求解

以倾斜轴双转台五轴联动机床结构为例，建立双转台五轴机床相关坐标系，如图 1所示。工件坐标系为OwXwYwZw，机床坐标系为OMXMYMZM，刀具坐标系为OtXtYtZt，Pivot R以及Pivot C分别是两旋转轴的旋转中心点。设靠近机床的旋转轴为第一旋转轴，如图1中所示的R轴。依赖第一旋转轴的旋转轴为第二旋转轴，如图1所示中的C轴。设倾斜轴 R轴在机床坐标系中的矢量为VR=VRxi+Vryj+Vrzk。

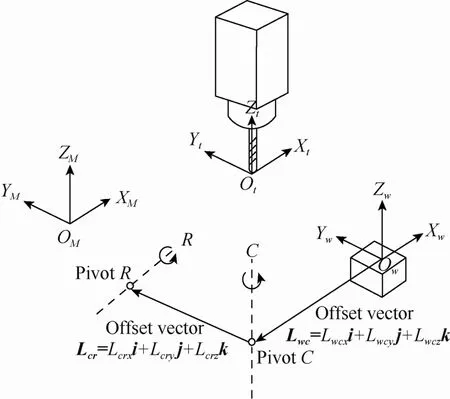
图1 双转台五轴机床坐标系

表示刀位文件中刀具矢量以及坐标点在工件坐标系中的矢量，并且刀位数据已知，则有[7]

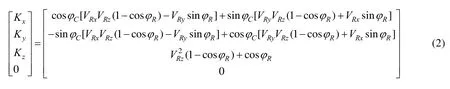
其中，式(1)、(2)在几何上都代表着切削刀具和机床之间相同的位置关系，而VR则代表着倾斜轴R轴在工件坐标系中的矢量，由上式中的第三项等式可得，R轴转角为

C轴转角为

1.2 转角优化选解

设 R轴的旋转行程范围为[θmin,θmax]，则第n(n=1,2,··)组刀位数据计算得出的 R轴旋转角 φRn的取值有以下几种情况：

(1) 若φRn在机床转角行程范围之外，即。在此情况下，无法对 R轴转角进行修正，此刀位数据无法进行加工，需修正或更换刀位文件及机床。

其中，

作为加工程序R轴旋转角度值。

(3) φRn在机床转角行程范围内，即此时取值则根据上一组刀位数据选取。计算，求得的解中对应的 φRn值为加工程序 R轴旋转角度值。根据以上所求的φRn，可以确定对应的C轴旋转角度为

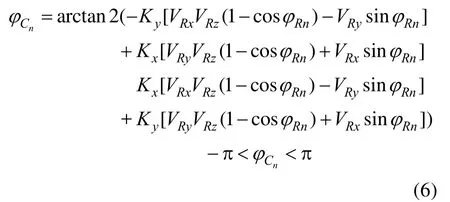
以旋转路径最短为原则，根据当前刀位数据的前后旋转角度 φCn-1及φCn+1，对C角度进行简单优化处理。取预设修正值φC′n=φCn±2π。φCn为正值时取负号，φCn为负值时取正号。

n

通过以上对转角选解的优化处理，避免了因选解不当引起的超程问题，并使得旋转轴旋转路径最短，路径平滑。

1.3 奇异区域的处理

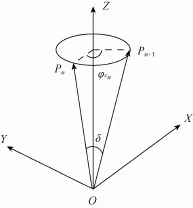
图2 奇异区域刀轴矢量与旋转角度关系

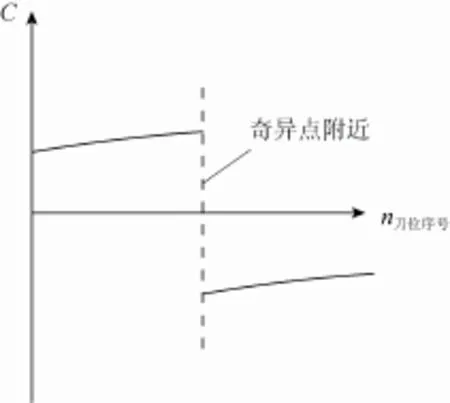
图3 奇异区域旋转角度变化

在奇异区域，较大的旋转步距会导致实际加工中较大的非线性误差，甚至可能会导致刀具与机床、刀具与工件的干涉与碰撞等问题，因此需要对求得的旋转角度进行修正优化处理。如果对其进行线性插值，则会引起 C轴旋转速度发生突变(图4中S1曲线部分)。本文采用三次样条曲线的方式进行插值，在奇异区域插入若干刀位点(图4中S2曲线部分)，使得C轴旋转角度接近奇异区域时，C轴旋转速度呈几何连续，转角能够平滑过渡，且转速不会发生突变，减小对机床的冲击。在插值点处计算相邻插值点的非线性误差，并对不满足非线性误差要求的刀位点进行线性插值，从而减小 C轴大步距转动带来的较大的非线性误差，如图4所示。

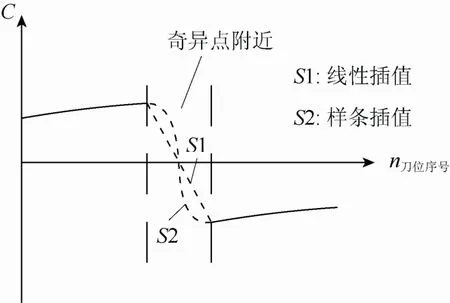
图4 奇异区域插值方式比较

算法描述如下：

(1) 计算插值的边界切矢条件。通过对奇异区域范围检测，设定奇异区域的初始刀位点为，经机床运动学转换后的NC加工数据位，结束刀位点为，经机床运动学转换后的加工数据。其中，Ps、Pe坐标与1.1节中的刀位数据一样，Xps、Yps、Zps以及Xpe、Ype、Zpe分别为刀尖的中心的位置的分量，is、js、ks以及ie、 je、ke刀具方向的分量，Ms、Me与Ps、Pe对应的机床数控代码加工数据位。R、C坐标即为转角φR、φC。因为5个轴同时从当前位置Ms移动到随后位置Ms+1，假定每个轴在指定点之间做线性移动。因此，在Δt的间隔时间下实际的弯曲路径中可计算出入奇异区域的各坐标变化切矢为

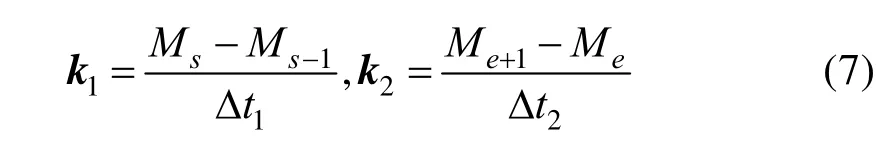
作为曲线插值的边界条件，其中，t为虚拟时间轴；Δt 间隔时间。

(2) 计算三次样条插值曲线。将k1、k2的值作为边界切矢条件， Ms -1，Ms，Me， Me+14个点作为曲线上的点，对Ms，Me进行三次样条插值，得到插值曲线s(t)。根据加工精度的要求以及机床产生颤振的条件，计算所需插值点的个数n，从而获得各个插值点数据Ms+1,Ms+2,… ,Mi,…,Me-1, Me。

(3) 对不满足非线性误差的点进行插值。计算相邻插值点的非线性误差[8-9]，若非线性误差超出允许范围，则需要对其进行再次插值。设不满足非线性误差的插值点为 Mi, Mi+1，对两点进行线性插值。取插值点Mi′，则有

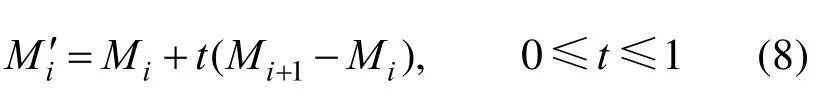
其中，t为虚拟时间轴。

重新计算Mi，′及′， Mi+1之间的非线性误差，若不满足要求，则根据以上所述方法在不满足非线性误差要求处继续进行插值。

需注意的是，在对 C轴旋转角度进行插值的过程中，由于 C角变换引起的干涉等并不能通过插值进行减小或消除，需要对NC加工数据进行刀具位置优化。根据上文所述，在奇异区域，刀具轴向矢量近似平行于C轴。给定安全距离值ΔA，将刀轴矢量沿刀轴方向平移到远离当前加工平面Δ A的距离，即

离开奇异区域后将当前插值获得的坐标转换为原来的NC线性轴坐标，即

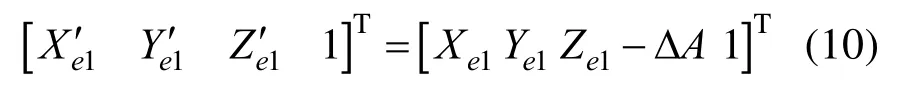
流程如图5所示。流程图中“根据R、C求解X、Y、Z坐标”的详细过程在文献[4]中已有详细说明：所期望的NC数据(表示为X，Y和Z)的可以通过考虑两个旋转矢量 R、C来获得，同时在、该文中给出了求解X、Y、Z坐标的表达式，这里不再赘述。

图5 算法流程

2 实例验证

本文以叶片加工作为实例进行验证。CATIA加工模型输出的部分加工刀位数据如表1所示。

表1 叶片模型加工部分刀位数据(mm)

以45°倾斜B轴DMG DMU50V五轴倾斜转台机床为例，其相应的数控系统为 Heidenhain iTNC 530。其旋转轴R的矢量为[0, 0.707107, 0.707107]T，为简便起见，设编程坐标系与工件坐标系重合。则经过机床运动求解得到相应的Heidenhain iTNC 350的加工数据如表2所示。

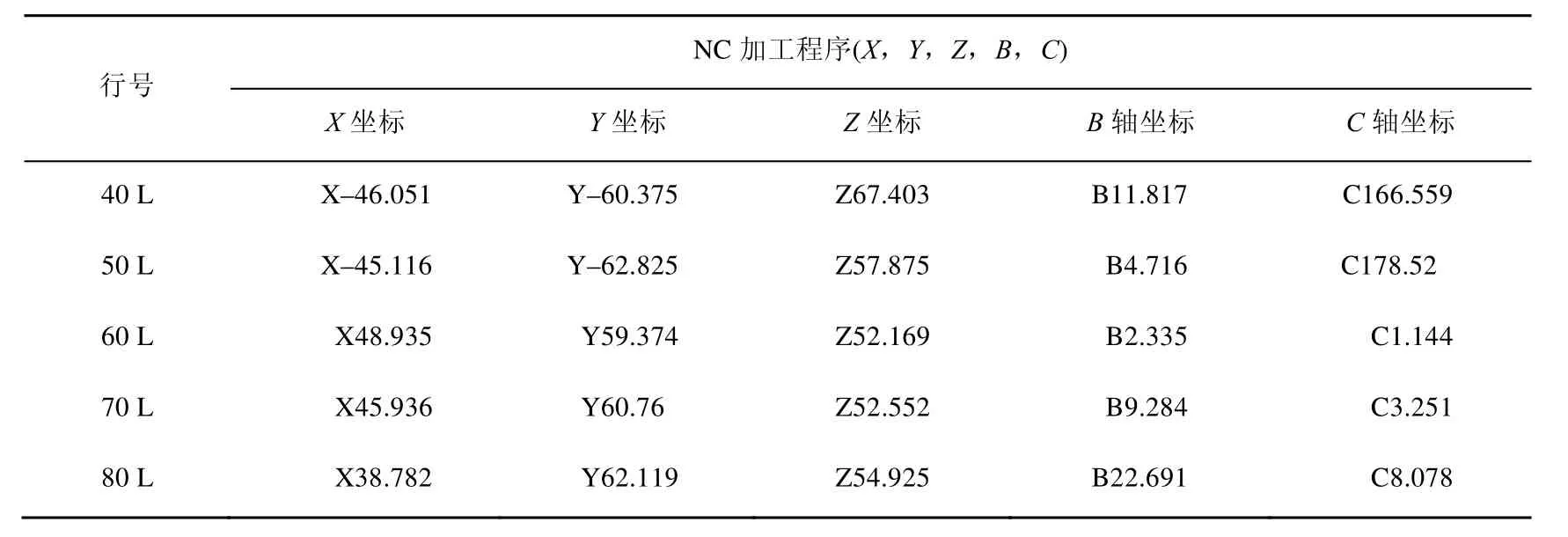
表2 奇异区域根据运动学求解得到的NC程序(mm)

根据前后计算结果，R轴选解均取正值。可以看出，第2、3组刀位数据点计算得出的C轴旋转角度与前后刀位数据对应的旋转角度相差很大，并且在修正2π角度也无法解决问题。

采用三次样条插值方法进行插值后，得到的各线性轴及旋转轴的插值曲线如图6所示。

图6 插值曲线

根据计算获得的插值曲线以及机床不发生颤振的条件，等距选取其中的 5个插值点，根据开发的后置处理系统，获得最终的Heidenhain iTNC 350数控系统的加工数据如表3所示。

表3 处理后得到的NC程序(mm)

表2、3中的“B”同前文中的“R”。采用该种方法获得的NC加工程序用来加工叶片，经Vericut仿真取得了较好的效果，如图7所示。

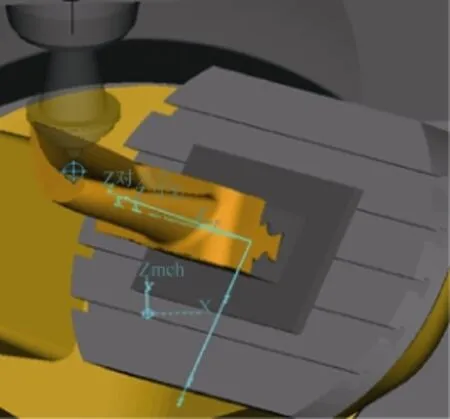
图7 Vericut叶片加工仿真

3 结 论

本文在对五轴机床旋转/摆动轴的求解进行优化选择，并对奇异区域的加工数据进行样条插值，对于相邻插值点处不满足非线性误差的加工数据进行线性插值，提高加工精度，解决了因后置处理中选解不当引起的碰撞、旋转轴在相邻刀位之间步距过大以及在奇异区域旋转轴产生急速转动、非线性误差过大等问题。经Vericut仿真验证效果良好。

[1] Affouard A, Duc E, Lartigue C, et al. Avoiding 5-axis singularities using tool path deformation [J]. International Journal of Machine Tools and Manufacture, 2004, 44(4): 415-425.

[2] Sørby K. Inverse kinematics of five-axis machines nearsingular configurations [J]. International Journal of Machine Tools and Manufacture, 2007, 47(2): 299-306.

[3] 杜 娟, 闫献国, 田锡天. 复杂曲面五轴加工局部干涉处理技术研究[J]. 图学学报, 2012, 33(1): 113-121.

[4] She C H. Huang Z T. Postprocessor development of a five-axis machine tool with nutating head and table configuration [J]. The International Journal of Advanced Manufacturing Technology, 2008, 38(7): 728-740.

[5] 王 峰, 林 浒, 郑飂默, 等. 五轴加工奇异区域的检测和处理[J]. 计算机集成制造系统, 2011, 17(7): 1435-1440.

[6] 郑飂默, 林 浒, 盖荣丽, 等. 五轴数控系统旋转轴快速平滑插补控制策略[J]. 机械工程学报, 2011, 47(9): 105-111.

[7] 王 峰, 林 浒, 刘 峰, 等. 五轴加工奇异区域内的刀具路径优化[J]. 机械工程学报, 2011, 47(19): 174-180.

[8] 王 丹, 陈志同, 陈五一. 五轴加工中非线性误差的检测和处理方法[J]. 北京航空航天大学学报, 2008, 34(9): 1003-1006, 1091.

[9] 杨旭静, 周元生, 陈泽忠, 等. 五轴数控加工中旋转轴运动引起的非线性误差分析及控制[J]. 机械工程学报, 2012, 48(3): 140-146.

Research on Optimization of Rotation Angle and Singular Area Handling in Five-Axis Post-Processing

Yu Dan, Yan Guangrong, Fan Qingxiang, Ding Tao, Xu Xiangyu

(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)

Post-processing is the key of the transformation from CL-Data of CAM system to NC program. Since the improper selection of rotation angle will leads to collision between cutter tool and work piece and dramatic change of rotary axis in adjacent cutter-location as well as rotary angle

five-axis NC manufacturing; post-processing; optimization of rotation angle; singular area handling

V 260.6

10.11996/JG.j.2095-302X.2016050614

A

2095-302X(2016)05-0614-06

2016-01-13；定稿日期：2016-04-28

科技重大专项支持项目–高档数控机床与基础制造装备(2013ZX04012021)

余 丹(1991–)，女，江西九江人，硕士研究生。主要研究方向为航空宇航制造工程。E-mail：yudanbuaa@126.com

闫光荣(1969–)，男，重庆人，副研究员，博士。主要研究方向为计算机辅助设计与制造、计算机图形学。E-mail：yangr@buaa.edu.cn

changes rapidly and non-linear error exceeds allowable limits in singular area. This paper proposed a method which integrates optimization of rotation angle and singular handling in five-axis post-processing. A post-processor was developed with C++ program language based on the method, which inputs the CL-Data of CATIA NC manufacturing module and outputs the NC program. The validity of the method is verified through Vericut simulation.