基于曲面精确表示的距离极值点的计算及在刀具干涉检测中的应用
2016-12-02田素凯陈志同
田素凯, 宁 涛, 陈志同
(北京航空航天大学机械工程及自动化学院,北京 100191)
基于曲面精确表示的距离极值点的计算及在刀具干涉检测中的应用
田素凯, 宁 涛, 陈志同
(北京航空航天大学机械工程及自动化学院,北京 100191)
针对基于曲面精确表示的刚体碰撞检测中裁剪曲面距离极值点的求解问题,提出了利用平面向量场估计初始曲面距离极值点的方法,避免了曲面过度细分,讨论了距离极值点满足的微分几何条件,给出了解析曲面/参数曲面、参数曲面/参数曲面、点/参数曲面和曲线/参数曲面的距离极值点迭代算法。实例验证分析了该算法的高效性和可靠性。
碰撞检测;平面向量场;距离极值点;迭代
碰撞检测(collision detection)是指判断多个刚体(零件、机械设备等)所占据的空间是否有重叠区域,一直是计算机仿真、干涉检查、数控加工、机器人控制和虚拟现实等学科的关键技术。现有文献中的碰撞检测算法分为基于图形[1]和基于图像[2]两大类检测算法。基于图形的碰撞检测包括模型分解(modal decomposition)和空间分解(space decomposition)两种,前者常用方法有 AABB(axis aligned bounding box)层次树[3]、包围球(bounding ball)层次树、OBB(oriented bounding box)层次树和K-DOPs法(discrete orientation polytopes)[4]等;后者利用GPU硬件的加速功能对多面体模型进行凸分解,进而提高碰撞检测的效率。这些算法都是基于模型离散或空间分解的方法,在精确性和实时性方面有一定的欠缺,无法解决最大过切、欠切位置计算等问题。近年来,针对曲面精确表示
的刚体碰撞检测算法的研究有一定的进展,Choi[5]给出了空间椭球体的碰撞条件;Odehnal[6]研究了两个圆环面的共线法矢;Lopes等[7]提出了二次曲面和超二次曲面的碰撞检测数学框架;Zeng等[8]给出了支持多种几何体的碰撞检测算法库。由于CAD系统支持的曲面有十多种之多,而以上方法仅适用于几种简单解析曲面,因此基于曲面精确表示的刚体碰撞检测算法尚待研究。
在曲面精确表示的刚体碰撞检测算法中,曲面之间的距离极值点对应最大干涉(过切、欠切)位置,相关计算是碰撞检测算法的关键。现有曲面间最小距离的求解主要有离散法和解析法,算法的实现效率及其精确度是两个重要的性能指标。Gilbert和Foo[9]的算法首先将曲面离散为三角片,然后再计算两三角片的最近距离,进而获取两曲面的近似距离。当精度要求比较高时,该算法的效率较低。Johnson和Cohen[10]提出了一种计算曲面间最小距离的框架,该框架以包围盒细分为基础,算法效率较低。Sohn等[11]提出了一种线性几何(line geometry)的方法求解曲面间距离的计算,该算法减少方程组和未知量的数量,提高了算法效率,尤其适用于求解二次曲面距离极值点。刘浩等[12]提出了一种计算双二次 NURBS曲面的最近距离点。文献[11-12]都没有给出一般曲面间距离求解的具体算法。陈丽萍等[13]从极值点的几何条件出发,利用赋范空间投影法迭代,求取自由曲线到曲面的极值距离,但该算法并没有给出初始点的计算方法。
本文结合平面向量场提出了一种求解裁剪曲面的初始距离极值点的算法[14-15],该算法利用裁剪曲面的三角剖分网格,依据平面向量场的Poincare公式,估算出单张三角片内部是否有距离极值点。分别针对解析曲面/参数曲面、参数曲面/参数曲面等情况,给出了距离极值点迭代求精算法。同时,还讨论了点到曲面距离、曲线到曲面距离的求解算法。
1 初始距离极值位置点的估计
在数控加工几何仿真等领域,需要计算平面、二次曲面及圆环面等代数曲面与参数曲面距离极值位置。如何利用裁剪曲面的三角网格、基于平面向量场技术估计初始距离极值点,需引入几个基本概念:
(1) 平面向量场[15]v是连续函数 v:D →R2,即对于平面区域D中的任何点p,v定义平面向量v(p)与之对应。向量场在自然界广泛存在,例如引力场、重力场、电磁场和流体的速度场等。在微分动力系统中,微分方程的稳定性用向量场刻划[16]。对于平面区域D中一点 p,若v(p)=0,则称p为平面向量场v的临界点(critical point)。假设p为平面向量场v的孤立临界点,N为p的领域,且在N及其边界∂N上没有其他临界点。对于边界∂N 上的每个点q,平面向量场v都定义非0向量v(q)与之对应。假设一个手持指南针的人,沿逆时针方向在边界上行走,指南针总保持与向量场同向。当回到出发点时,指南针亦回到初始位置。所以在此过程中,指南针相对于底盘必转动整数圈。逆时针转一圈记为1,顺时针转一圈记为–1。逆时针和顺时针所转圈数的代数和称为旋转数,如图 1所示。向量场的旋转数可以用 Poincare公式[16]计算:,其中C是平面区域中的封闭曲线,在 C上向量场▽φ = (φu,φv)非退化。有定理:设v是连续的平面向量场,C为 v上封闭简单光滑曲线,若旋转数W(v,C)不为0,则闭曲线C内至少有一个临界点。临界点和旋转数反映向量场v的拓扑结构。当向量场v发生微小变动时,其拓扑结构一般保持不变,所以向量场的拓扑结构被认为是一种稳定的结构,能反映向量场的内在性质。

图1 平面向量场的旋转数
Kriezis等[14]用有向距离函数定义平面向量场。如图2所示,假设点p是曲面 S1(u,v)上的任意一点,则q为曲面 S2(s,t)上距离点p最近的一点。当曲面 S1(u,v)上的点 p变动时,得到映射M(p )=q。对于曲面 S1(u,v)上任意一点p,S1(u,v)
有向距离函数定义为:φ(u,v) =(n2(M (p)), p -M(p) ),其中( , )表示内积n2,n2表示曲面S2(s,t)的单位法向量。有向距离函数 φ( u,v)的梯度定义了u、v参数域上的向量场,在 φ( u,v)的有效定义域内,有 ▽φ (u,v) =((n2,S1u),(n2,S1v))。所以对于 φ( u,v)的任何临界点(u, v),有 (n2,S1u) =0, (n2 ,S 1v)=0。

图2 有向距离函数的定义
(2) 讨论距离极值点的估算方法。在以上有向距离函数的定义中,假设 S1(u,v)、 S2(s,t)是裁剪参数曲面, Ω1=(V1,T1)、Ω2=(V2,T2)分别是两裁剪曲面的三角片集合,其中 Vi表示所有顶点集合,Ti表示所有三角片集合,i=1,2。利用 S2(s,t)的三角片集合,使用点/三角片最近距离算法计算出顶点集合 V1中每个顶点对应的 φ(u,v)。对于三角片集合T1中的任何三角形,假设v1,v2,v3是其3个顶点对应的平面向量场φ(u,v)的3个矢量,如果对某个i=1,2,3成立,则该三角形内可能存在距离极值点,否则计算v1和v2,v2和v3,及v3和v1的夹角之和α,若,则该三角形内可能存在距离极值点。这里“v1和 v2夹角”是指向量v1按逆时针转到另向量v2的夹角,如图3所示。
如果 S2(s,t)退化为一个三维点,则无须利用Ω2=(V2,T2),可直接计算出有向距离φ( u,v)在三角片网格 Ω1=(V1,T1)上的取值,进而得到对应的平面向量场;如果 S2(s,t)是二次曲面或圆环面,则由于 S1(u,v)上的任意点p到 S2(s,t)上最近点q容易计算,所以可以用解析方法得到▽φ(u,v) =((n2,S1u),(n2,S1v))。后续对距离极值点的估计同上给出的参数曲面到参数曲面距离极值点的算法。

图3 向量场中向量夹角的计算
2 距离极值点的迭代算法
以上提出了一种针对代数曲面和裁剪曲面的初始极值位置点的估计方法。表 1针对具体的代数曲面,构造对应的迭代公式,可实现初始极值位置点的迭代求精。
说明:
(1) 图示中S(u,v)代表参数曲面S(u,v),n(u,v)代表曲面上某点处的法向量,G(t)为参数曲线。
(2) 对于球面与参数曲面的情况,给定球心为O(x0,y0,z0),及参数曲面S(u,v),曲面上各点处单位法矢为 n( u,v)。曲面 S(u,v)的法矢方程为L(s) = S(u,v) +s ·n( u,v),要找到这样的u, v参数,使L(s)通过球心O。在L(s)上找一点距离O最近,由于

所以L(s)与球心O的最近距离为 (V,V )-(n,V )2,其中 V =S-O。基于以上分析令迭代目标函数为f(u,v) = (V,V ) -(n,V )2,求导得
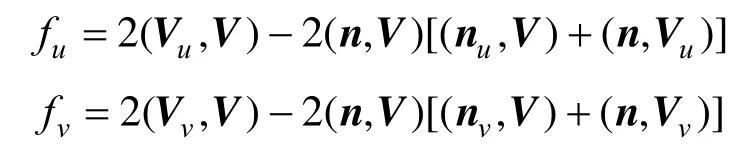

表1 迭代公式
(3) 对于圆柱面与参数曲面的情况,令给定的圆柱面轴线为 P(t)=P+tD,其中P是圆柱轴线上一点 (x0,y0,z0),D是圆柱轴线单位方向,给定参数曲面 S(u,v),曲面上各点处单位法矢为 n(u,v)。曲面 S(u,v)的法矢方程为 L(s) = S(u,v) +s ·n(u,v),要使L(s)也是圆柱面的法矢,则L(s)必须与圆柱面轴线P(t)交于一点,且满足(n(u,v),D) =0。考虑到两直线L(s)和P(t)上两点距离之平方,令

其中, V =S-P ,对g(s,t)求偏导得


所以两直线的最近距离点对满足

解此方程得

其中, Δ=1 -(D,n)2,将上式中的s, t代入g(s, t)得直线L(s)与P(t)的最近距离为

所以迭代目标函数定义为

f(u,v)为L(s)与P(t)最近距离的平方加上L(s) 与P(t)夹角余弦的平方。实际上,当(n,D )→0时,Δ→ 1,于是迭代目标函数 f(u,v)可简化为

对于 f(u,v)求偏导得

利用上面的导数构造迭代公式:
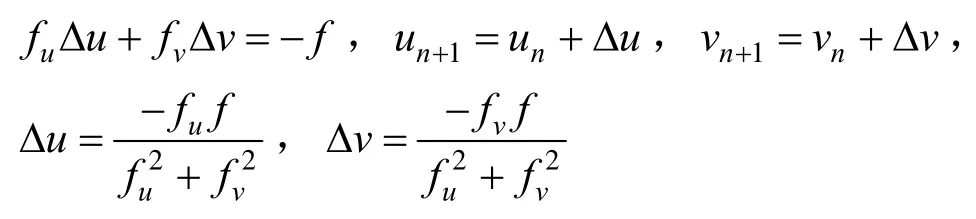
(4) 对于圆环面与参数曲面情况,令给定的圆环面中心圆方程为: Q (θ) =O+ rX cosθ + rY sinθ,给定参数曲面 S(u,v),曲面上各点处单位法矢为n( u,v)。由于圆环面与参数曲面的极值位置点对连线垂直于曲面一阶偏导数Su和Sv,且与中心圆的切矢垂直,所以定义目标函数为

3 距离极值点算法应用
在数控加工几何仿真领域,为计算过切量和确定过切位置,需要计算平面、二次曲面及圆环面等代数曲面与参数曲面极值位置。本文实现了平面、圆柱面、球面和圆环面对参数曲面的极值位置计算算法,并结合平面向量场技术和裁剪曲面剖分,实现了三坐标加工过切仿真功能。测试实例为:B样条曲面u, v参数的次数都是5次,控制顶点是 30×30个,x, y, z最小最大范围分别为[–134,134]×[–133,136]×[–172,77],单位为mm,如图4所示。以φ10球头刀为刀具采用变步长方法计算刀位轨迹,其逼近 B样条曲面等距面的精度为0.001,刀位点总计64 976个。裁剪曲面的三角片总计8 818个,三角片结点共4 458个。

图4 B样条曲面及其裁剪部分
在仿真算法中,两个相邻刀位点之间的刀具包络体分为球体和圆柱体两部分处理,如图 5所示。由于此算法中三角片和刀位点数据量很大,为提高搜索与两个相邻刀位点之间的刀具包络体邻近的三角片,在加工坐标系xoy坐标面上划分正方形网格单元(边长等于刀具半径),构建三角片相邻关系索引表。该方法大幅减少了三角片的查询计算量和时间。

图5 单条插补段的刀具运动包络体
仿真环境是Windows 7,处理器是Intel Core Duo P8600,主频是2.4 GHz,内存2 G。仿真结果如图6~7所示。最大过切量是0.000 86 mm,耗时
46.4 s,见表2,过切基本出现在参数曲面曲率大的位置,且为刀具包络的圆柱部分与零件曲面干涉,刀具包络的球面部分与零件无干涉。仿真结果表明本文实现的代数曲面/参数曲面极值位置计算算法稳定可靠,能够实现加工过切仿真等CAD/CAM功能。

图6 裁剪曲面及其刀位轨迹

图7 放大10 000倍的过切情况

表2 测试结果
4 结 论
现有成熟的碰撞检测算法都是基于模型离散或空间分解的算法,难以解决给出最大干涉量和干涉位置等问题,而基于曲面精确表示的碰撞检测则可以解决这样的问题,但相关算法更为复杂。本文研究了点、线、面到裁剪曲面的距离极值点求解问题,给出了一种通用算法思路。该算法基于裁剪曲面的三角片网格、利用平面向量场估算初始距离极值点,再通过Newton迭代精确的距离极值点。对于二次曲面及圆环面/参数曲面的情况,由于二次曲面及圆环面的几何特性,相关平面向量场以及Newton迭代的计算大为简化。后续研究内容主要包括二次曲面及圆环面之间的距离极值点的求解问题,以及基于曲面精确表示的碰撞检测系统的框架设计。
[1] Lin M C, Gottschalk S. Collision detection between geometric models: a survey [C]//Proceedings of IMA Conference on Mathematics of Surfaces, Cambridge: Andalucia En La Historia, 1998: 37-56.
[2] 范昭炜, 万华根, 高曙明. 基于图像的快速碰撞检测算法[J]. 计算机辅助设计与图形学学报, 2002, 14(9): 805-809.
[3] 陈 华. 确定任意形状物体最小包围盒的一种方法[J].图学学报, 2010, 31(2): 49-53.
[4] Klosowski J T, Held M, Mitchell J S B, et al. Efficient collision detection using bounding volume hierarchies of k-DOPs [J]. IEEE Transactions on Visualization & Computer Graphics, 1998, 4(1): 21-36.
[5] Choi Y K. Collision detection for ellipsoids and other quadrics [D]. Hong Kong: The University of Hong Kong, 2008.
[6] Odehnal B. Common normals of two tori [J]. Journal for Geometry & Graphics, 2005, (9): 51-65.
[7] Lopes D S, Silva M T, Ambrósio J A, et al. A mathematical framework for rigid contact detection between quadric and superquadric surfaces [J]. Multibody System Dynamics, 2010, 24(3): 255-280.
[8] Zeng L, Ning T, Xi P. Research and application of general collision detection simulation platform [M]//The 19th International Conference on Industrial Engineering and Engineering Management. Berlin: Springer Berlin Heidelberg, 2013: 1315-1323.
[9] Gilbert E G, Foo C P. Computing the distance between general convex objects in three-dimensional space [J]. IEEE Transactions on Robotics & Automation, 1990, 6(1): 53-61.
[10] Johnson D E, Cohen E. A framework for efficient minimum distance computations [C]//IEEE International Conference on Robotics & Automation. New York: IEEE Press, 1998: 3678-3684.
[11] Sohn K A, Juttler B, Kim M S, et al. Computing distances between surfaces using line geometry [C]// Computer Graphics and Applications, 2002. Proceedings. Pacific Conference on. New York: IEEE Press, 2002: 236-245.
[12] 刘 浩, 唐月红, 廖文和. 双二次NURBS曲面间的最短距离[J]. 计算机辅助设计与图形学学报, 2003, 15(10): 1298-1302.
[13] 陈丽萍, 陈 燕, 胡德金. 一种快速完备的自由曲线和曲面间最短距离求取算法[J]. 上海交通大学学报, 2003, 37(S1): 41-44.
[14] Kriezis G A, Patrikalakis N M, Wolter F E. Topological and differential-equation methods for surface intersection [J]. Computer-Aided Design, 1992, 24(1): 41-55.
[15] 宁 涛, 马德昌, 王亚平, 等. 平面向量场与曲率分析在曲面求交中的应用[J]. 计算机学报, 1997, 20(12): 1074-1080.
[16] 张锦炎, 钱 敏. 微分动力系统导引[M]. 北京: 北京大学出版社, 1991: 41-47.
On Computation of Distance Extremum Points Based on Exact Surface Representation and Its Application in Tool Interferance Detection
Tian Sukai, Ning Tao, Chen Zhitong
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)
Aiming at the problem of solving distance extreme points on trimmed surfaces in collision detection of rigid bodies which are represented by exact surface, a method is presented to obtain the initial distance extreme points using the plane vector field, which can avoid the excessive subdivision of the surface. The differential geometry conditions of the distance extreme points are discussed, and iterative formulas for obtaining distance extreme points of the analytic surface/parametric surface and parametric surface/parametric surface are given in this paper. The efficiency and reliability of the algorithm are verified by an example.
collision detection; plane vector field; distance extreme points; iteration
V 260.5;TP 391
10.11996/JG.j.2095-302X.2016050620
A
2095-302X(2016)05-0620-06
2016-03-24;定稿日期:2016-05-13
国家科技重大专项–高档数控机床与基础制造装备科技重大专项课题(2013ZX04011031)
田素凯(1989–),男,山东枣庄人,硕士研究生。主要研究方向为计算机辅助设计、CAD技术。E-mail:tskdqq@163.com
宁 涛(1966–),男,辽宁丹东人,副教授,博士。主要研究方向为计算机辅助设计、CAD/CAM技术。E-mail:ningtao@buaa.edu.cn
