二维点轮廓与矢量轮廓配准研究
2016-12-02陈志同沈云超
黄 方, 宁 涛, 陈志同, 沈云超
(北京航空航天大学机械工程及自动化学院,北京 100191)
二维点轮廓与矢量轮廓配准研究
黄 方, 宁 涛, 陈志同, 沈云超
(北京航空航天大学机械工程及自动化学院,北京 100191)
在平面类零件的光学测量中,二维点轮廓与矢量轮廓的配准是关键算法,配准精度直接影响测量精度。针对平面类零件的配准问题,提出了基于形状特征函数的粗配准算法和二维矢量最近点迭代(ICP)精配准算法。利用角度距离图法将矢量图形的几何信息转化为独立于坐标系的连续函数,进而实现粗配准算法。基于平面上点与曲线的最近距离算法计算配准目标函数,给出了不同于传统的ICP算法的直接求解目标函数的解析方法,有效提高了算法效率。利用实例验证分析了该算法的高效性和可靠性。
二维矢量图形;二维点云;粗配准;精配准;最近点迭代算法
平面类零件的制造过程中存在误差,如何快速测量零件的尺寸,并与加工的数据进行对比,得到加工误差,对判断加工的正确性以及提高加工效率至关重要。受测量工具和测量者的影响,传统的人工测量方法效率低,而且可能对零件造成损伤。三坐标测量仪的效率会随着测量点数的增加而下降,点数多的情况下耗时也多。使用光学测量的方式能够很快获取零件的轮廓图,进而实现快速的尺寸测量与对比。英国Inspect Vision公司的Planar视觉检测系统就使用了这种测量手段,
采用超高分辨率的成像系统,瞬间获取零件的测量数据,通过计算机处理,生成零件的实际点轮廓图,与零件的CAD图形进行对齐,显示各部位的尺寸偏差,从而获取零件的加工精度。在尺寸的测量和对比过程中,需要实现零件的点轮廓图和加工CAD图的对齐,这个处理叫做配准。配准是一个带有约束条件的最优化问题,是在平移和旋转组成的刚体变换的约束下达到最佳对齐。元素可以是曲面、点云以及二维矢量图形。配准分为粗配准和精配准两步。通过粗配准使得待配准元素近似对齐,为精配准提供一个良好的初始位置,精配准在粗配准基础上通过迭代,逐步逼近最佳对齐。
现阶段常用的粗配准方法有:三点对齐法、力矩主轴法、遗传算法、最小包围盒法以及标签法等。张学昌等[1]提出了三点对齐法进行粗配准,简单直观快速。力矩主轴法也被用来解决粗配准问题[2]。严庆光等[3]使用了遗传算法实现粗配准。刘斌等[4]使用了最小包围盒算法。标签法则是在测量时提前设置一些特征点,然后在配准时使用这些特征点[5]。
Besl和 Mckay[6]提出的最近点迭代(iterated closest point,ICP)算法被广泛应用于解决精配准问题。传统的 ICP算法有配准精度上的保证,但其效率不高,所以出现了很多改进的 ICP算法。改进的 ICP算法主要有以下几方面:点对的选取,距离度量的选取和搜索策略的选取[7]。传统的ICP算法每次迭代计算使用全部的点。为了减少每次迭代中用于计算的点,需要对配准元素进行采样,Turk和Levoy[8]使用了一致采样方法,Masuda等[9]使用的是随机采样方法。传统的 ICP算法把点到点的欧氏距离当作特征度量。Chen和 Medioni[10]利用的是测量点集中的点的法线与模型点集合的交点来确定对应点,得到对应点后,目标函数则采用的是点到面的距离。在对应点的选取,也就是构造各对应点的过程中,需要进行大量的搜索,时间复杂度为O(NcNx),其中Nc为测量点集中点数目,Nx为模型点集中点数目。这是传统ICP算法在配准效率上的瓶颈。Zhang[11]采用了多维二元搜索树(K-D Tree),使得时间复杂度降为O(NclogNx)。Jost和Hügli[12]提出了邻域搜索策略,时间复杂度为O(Nc)。蒋睿嵩等[13]根据配准模型中不同区域的重要性不同,引入权值约束,实现模型的高精度配准。王森等[14]通过引入稀疏度对模型进行配准优化,避免了局部对齐,提高了算法的稳定性和精确度。
已有算法是针对三维模型的配准,为了解决二维点轮廓与矢量轮廓的配准问题,本文提出一种二维粗配准算法以及一种二维快速 ICP算法。在粗配准阶段,根据点云和矢量图形内部相似的距离信息提出一种基于中心的角度距离图的粗配准算法,将几何形状映射为连续的周期函数,实现精度较高的粗配准。在精配准阶段,以点到曲线的距离为特征度量,以点与点到曲线的距离最近点为特征点对,以平移向量和旋转角度为目标,给出了一种解析求解方法,实现了二维ICP算法。其算法因为特征度量的选取以及目标参数的直接求解,在保证配准精度的基础上配准速度得到了极大提高。本文研究算法兼顾速度和精度,可应用在实际的平面零件检测中。
1 粗配准
针对二维配准的待配准元素做一些介绍,二维矢量图形是一个二维CAD图形,二维点云是根据二维矢量图形加工出来的平面零件经过成像以及轮廓提取之后得到的点轮廓。可称CAD图形的最外一环为二维矢量图形的外轮廓,其余部分称之为内轮廓,相应的点云中的最外一圈叫二维点云的外轮廓,其余部分称之为内轮廓。在粗配准时主要使用外轮廓的信息。
粗配准需要找二维点云和二维矢量图形的平移变换和旋转变换。先确定二维点云中心以及二维矢量图形中心的概念:以二维点云外轮廓所有点坐标的平均值为二维点云中心的坐标值;依据二维点云外轮廓点的数目对二维矢量图形外轮廓进行均匀离散处理,得到矢量图形外轮廓的点云,以矢量图形外轮廓的点云中所有点坐标的平均值为二维矢量图形中心的坐标值。对于平移变换,可以通过平移使得二维点云和二维矢量图形的中心重合来求取平移矢量。对于旋转变换,可以使用二维点云和二维矢量图形外轮廓的几何信息。二维矢量图形的旋转只与一个角度有关,因此可以考虑通过计算旋转角度来确定旋转矩阵。本文引入一个角度距离图的概念:对于一个图形,求得图形中心,计算图形外轮廓上任一点与方向向右的水平线的夹角,计算该点与点云中
心的距离,逆时针扫一周,以角度为自变量,以两点距离为因变量(如果同一个角度存在多个点,则取最远点计算距离),得到一个角度距离图。如图1、2所示。

图1 轮廓曲线1
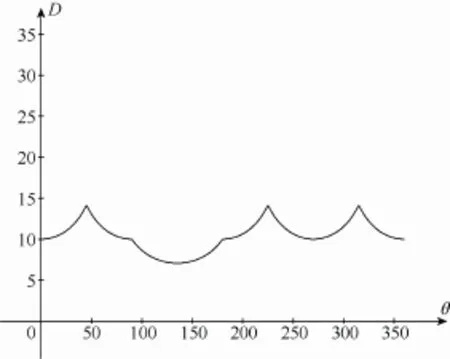
图2 角度距离图(一周)
对于两个只需做旋转变换的图形,旋转角度就是两个角度距离图的相位角。在外轮廓为非旋转对称图形时两个角度距离图曲线只相差一个相位角,而这个相位角就是旋转角度。在计算相位角时,采用最小二乘法,设置角度 θ,计算 θ在[0°,360°]变化时两个角度距离图对应角度的距离差的平方和。平方和最小的情况下,两个点云的角度距离图最佳对齐,得到的θ为所求得相位角。如图3~5所示。

图3 轮廓曲线2

图4 角度距离图(两周)

图5 相位角
在二维矢量图形的外轮廓为非旋转对称图形的情况下,称二维点云外轮廓部分为待配准点云,二维矢量图形外轮廓经过离散后得到的点云为模型点云。在实际求取角度距离图时的操作为:模型点云的角度计算范围是[0°,360°],待配准点云的角度计算范围是[0°,720°]。计算相位角时待配准点云与模型点云对应点的角度差为上文提及的θ。角度距离图法的流程图如图6所示。

图6 角度距离图法流程图
当二维矢量图形的外轮廓为非圆的旋转对称图形时,使用角度距离图法求得旋转角度之后旋转测量点云,外轮廓虽对齐,但内轮廓可能没有对齐,如图7所示。

图7 特殊情况
所以需要做进一步判断与处理。当二维矢量图形的外轮廓为非圆的旋转对称图形时,求出各旋转角,在使用角度距离图法粗配准的基础上,再比较以各旋转角做旋转变换的内部轮廓的对齐效果,选择最佳的旋转角度。
对齐效果的判断标准:称二维矢量图形外轮廓内部的封闭轮廓为矢量图形的内轮廓,称测量点云外轮廓内部的任一圈点云为测量点云的内轮廓,每一个内轮廓与外轮廓中心点的求法一致。求矢量图形每一个内轮廓中心点到所有测量点云内轮廓中心点中最近的中心点的距离,将所有距离加起来,得到一个距离值,距离值最小的情况即为最佳的对齐效果。
如果二维矢量图形的外轮廓为圆,内轮廓与外轮廓的对齐没有关系,所以角度距离图法失效。可以通过比较,0°~360°每一个角度逐步旋转时内部轮廓的对齐效果,选择最佳的旋转角度。
2 精配准
传统 ICP算法实现点云配准的基本思路是:假设两个点云P和M近似对齐,对于P中任一点,称M中的距离最近点为其对应点。在M中搜索P中任一点的对应点,得到点云X,计算P到X的刚体变换。进行迭代,直到满足要求或者达到最大迭代次数。假设P中点数目为Nc,pi为P中的点,mi为M中的点,所求的旋转变换为,所求平移变换为,则传统ICP算法的目标函数为

目标函数的求解主要有两种:①需要求解矩阵的特征值和特征向量,称之为为四元数方法;②需要进行矩阵奇异值分解,称之为SVD分解法。
本文的二维 ICP算法针对二维点云与二维矢量轮廓图。通过求取点到曲线的最近距离点来确定对应点对,本文处理二维的几何元素,在算法上做了一些简化,以平移矢量和旋转角度 3个变量为求解参数建立目标函数,可以使用解析方法直接求解方程。
二维ICP算法步骤如下:
步骤1. 设定参考数据集和目标数据集;
步骤2. 对目标数据集中的每个点,在参考数据集中寻找一个与之对应的最短距离的点;
步骤3. 建立匹配目标函数,对目标函数进行优化,求出目标函数最优解,得到新的目标数据集;
步骤4. 进行误差分析,若满足误差条件或达到最大迭代次数则转至步骤 5,否则,转至步骤2;
步骤5. 配准结束。
在求解变换这一步,先建立匹配目标函数,再对目标函数进行优化,求出目标函数最优解,从而得到新的目标数据集。以下是建立目标函数的过程:
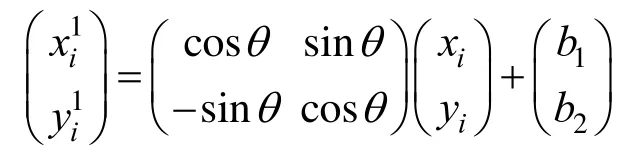
其中,θ、b1、b2为待定系数;为旋转矩阵;为平移向量。

求解待定系数θ、b1、b2,使得f最小。
下面为目标函数的求解过程
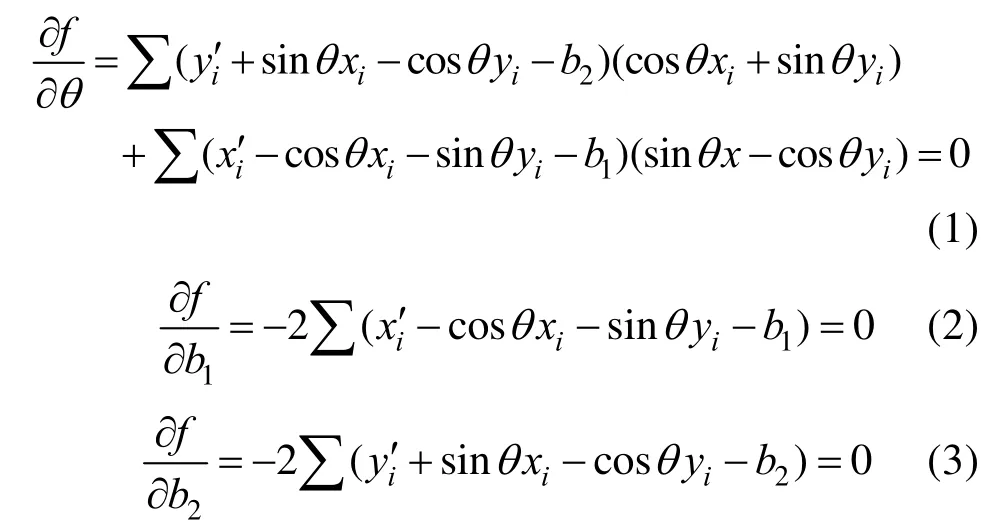
对这3个方程进行求解,由式(1)可得

由式(2)可得

由式(3)可得


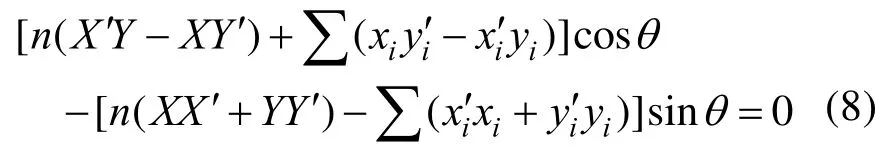
从而可得

将式(9)代入式(5)、式(6)可求b1、b2,得到θ、b1、b2的值,代入到方程

中可以得到新的目标数据点。
3 算法分析和实例验证
粗配准阶段的角度距离图法几何依据明确,主要使用外轮廓信息,对数据信息的部分缺失不敏感;计算简单直接,在保证配准的正确性的基础上耗时少,若测量点云数目为 Nc,则角度距离图法的时间复杂度为O(Nc);同时配准精度可以自主控制和调整,可以达到 1°甚至更精确。角度距离图法有两个缺点:①在矢量图形外轮廓为圆时失效;②在矢量图形外轮廓为旋转对称图形时,角度距离图法不能给出最终的结果,还要做后续的比较才能得到最终的结果。
精配准阶段的二维快速 ICP算法在寻找最近点这一步,采用求取点到曲线段的最近距离点来确定对应点对的策略,可以大大降低搜索最近点的时间复杂度,提高效率。测量点云数目为 Nc,矢量图形曲线段数目为N,时间复杂度为O(Nc)。对于测量点云数目为Nc,模型点云数目为Nx的情况,传统的 ICP算法搜索最近点的时间复杂度为O(NcNx)。同时原始的ICP算法,不能直接求取旋转矩阵和平移矩阵,需要使用四元数来表示旋转矩阵,再根据旋转矩阵求平移矩阵。目标函数的求解需要本文二维 ICP算法直接以旋转角度和平移分量为参数建立目标函数,原理清晰,形式简单,可以使用解析方法求解参数。二维快速 ICP算法适用于处理二维点云与二维矢量图形的配准,无法处理三维的配准,也不适合二维点云与二维点云的配准。
下面给出验证实例,其中根据矢量图形的外轮廓对称情况分为3类:外轮廓不对称、外轮廓为旋转对称图形和外轮廓为圆。配准误差是指配准后点
轮廓上点到矢量轮廓上对应点的距离的平均值。
所用计算机配置:处理器为 Inter Core i3-3240,CPU为3.40 GHz,内存4 GB。例子中黑色部分图形为平面零件的矢量图形,红色部分图形为点轮廓图。
实例1. 图形内轮廓一样,外轮廓不一样。根据外轮廓分为5种情况。
情况1. 图形外轮廓不对称之一(图8)。

图8 外轮廓不对称之一
情况2. 图形外轮廓不对称之二(图9)。

图9 外轮廓不对称之二
情况3. 图形外轮廓为旋转对称之一(图10)。

图10 外轮廓旋转对称之一
情况 4. 图形外轮廓为旋转对称之二(图11)。

图11 外轮廓旋转对称之二
情况5. 图形外轮廓为圆(图12)。

图12 外轮廓为圆
以上5种配准情况的配准信息如表1所示。

表1 实例1配准信息
由表1数据可知,当外轮廓为非圆的图形时,粗配准耗时很少,各情况下相差也极小,外轮廓为圆时,粗配准耗时增加,与之前的情况有接近10倍的差别,由此可确认角度距离图法的有效性。
实例2. 图形外轮廓一样,内轮廓不一样。根据内轮廓数目,分为3种情况。
情况1. 内轮廓数目为8(图13)。
情况2. 内轮廓数目为16(图14)。
情况3. 内轮廓数目为25(图15)。
以上3种配准情况的配准信息如表2所示。

图13 内轮廓数目为8

图15 内轮廓数目为25

表2 实例2配准信息
由表2数据可知,相对于传统ICP算法配准点集耗时较多,二维 ICP算法可称为快速精配准方法。在实验结果中精配准时间与点云中点数目的变化情况基本呈现线性的趋势,验证点云数目为Nc时,二维ICP算法的时间复杂度为O(Nc)。
4 结 论
(1) 针对二维点云图形与矢量图形的配准问题,论文提出了粗配准和精配准方法。在粗配准阶段,本文提出的角度距离图法将矢量图形的几何信息转化为连续的形状特征函数,此特征函数不依赖于坐标系,为粗配准提供了明确的配准依据。该方法计算量小、精度较高,易于用算法实现,但不足之处是无法解决外轮廓为圆的粗配准。
(2) 在精配准阶段,提出了针对点轮廓与矢量轮廓的二维快速ICP算法。该方法基于点/曲线的最近距离算法,极大提高了最近点的搜索效率,用解析方法直接求解本算法的目标函数,无需复杂的矩阵分解算法,即可得到最佳配准。
现有 ICP算法都是基于一种能量法,没有考虑到配准对象的局部几何形状。由于一般平面类零件中大量存在直角、圆等几何特征,在后续研究中将围绕点轮廓中的几何特征提取,以及几何特征的模糊匹配与配准展开。
[1] 张学昌, 习俊通, 严隽琪. 基于扩展高斯球的点云数据与CAD模型配准[J]. 机械工程学报, 2007, 43(6): 142-148.
[2] 黄镜荣, 李熙莹. 加快寻优的医学图像互信息配准算法的研究[J]. 中山大学学报: 自然科学版, 2005, 44(S2): 174-177.
[3] 严庆光, 李明哲, 李东成. 多点成形件检测中三维数据配准方法的研究[J]. 中国机械工程, 2003, 14(19): 34-37.
[4] 刘 斌, 华顺刚, 欧宗瑛, 等. 基于断骨模型自动配准的完全性骨折钢板预弯[J]. 光电子·激光, 2009, 20(7): 977-982.
[5] 罗先波, 钟约先, 李仁举. 三维扫描系统中的数据配准技术[J]. 清华大学学报: 自然科学版, 2004, 44(8): 1104-1106.
[6] Besl P J, Mckay H D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.
[7] Rusinkiewicz S, Levoy M. Efficient variants of the ICP algorithm [C]//Proceedings of the Third International Conference on 3D Digital Imaging and Modeling. New York: IEEE Press, 2001: 145-152.
[8] Turk G, Levoy M. Zippered polygon meshes from range images [C]//Conference on Computer Graphics and Interactive Techniques, SIGGRAPH. New York: ACM Press, 1994: 311-318.
[9] Masuda T, Sakaue K, Yokoya N. Registration and integration of multiple range images for 3-D model construction [C]//Proceedings of the 13th International Conference on Pattern Recognition. New York: IEEE Press,1996: 879-883.
[10] Chen Y, Medioni G. Object modeling by registration of multiple range images [C]//Proceedings of IEEE Conference on Robotics and Automations. New York: IEEE Press, 1991: 2724-2729.
[11] Zhang Z Y. Iterative point matching for registration of free-form curves and surfaces [J]. International Journal of Computer Vision, 1994, 13(2): 119-152.
[12] Jost T, Hügli H. Fast ICP algorithms for shape registration [M]. Berlin: Springer, 2002: 91-99.
[13] 蒋睿嵩, 魏发远, 冯大勇, 等. 一种权值约束的精确配准算法[J]. 图学学报, 2014, 35(2): 167-172.
[14] 王 森, 王 璐, 洪靖惠, 等. 基于Sparse ICP的三维点云耳廓识别[J]. 图学学报, 2015, 36(6): 862-867.
Registration of Planar Point Cloud and Vector Graphics
Huang Fang, Ning Tao, Chen Zhitong, Shen Yunchao
(School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)
In the optical measuring of planar parts, the registration of 2D point contour and planar vector contour is the key algorithm, the speed and precision of registration has a major impact on the speed and precision of measure result. In order to solve the problem of registration of 2D point cloud, a coarse registration algorithm based on shape feature function and a 2D iterated closest point (ICP) fine registration algorithm are researched. Through the angle-distance graph, geometry information of point contour and planar vector contour is translated to continuous function that is independent of coordinate system. The objective function of registration is calculated on account of nearest distance algorithm on planar point and curve, and analytic method of solving the objective function directly is given, which is different from traditional ICP algorithm. The efficiency of algorithm is improved significantly. Examples are exhibited to analysis the efficiency and reliability of the algorithm.
planar vector graphics; 2D point cloud; coarse registration; fine registration; iterated closest point algorithm
V 260.5; TP 391
10.11996/JG.j.2095-302X.2016050598
A
2095-302X(2016)05-0598-09
2016-03-10;定稿日期:2016-05-03
国家科技重大专项–高档数控机床与基础制造装备科技重大专项课题(2013ZX04011031)
黄 方(1991–),男,湖南娄底人,硕士研究生。主要研究方向为计算机辅助设计、CAD技术。E-mail:hf501x@163.com
宁 涛(1967–),男,辽宁丹东人,副教授,博士。主要研究方向为计算机辅助设计、CAD/CAM技术。E-mail:dr.nt@163.com
