基于离散元法的长短轴之比对散粒材料抗剪强度影响分析

龚 健， 刘 君

( 大连理工大学 水利工程学院, 辽宁 大连 116024 )



基于离散元法的长短轴之比对散粒材料抗剪强度影响分析

龚 健， 刘 君*

( 大连理工大学 水利工程学院, 辽宁 大连 116024 )

杆状颗粒由于其形状与砾石、药品和谷物等真实颗粒的形状接近而受到研究者们的关注，其形状特征常用长短轴之比进行表征．以往许多学者曾通过离散元法研究过在相同孔隙率下杆状颗粒长短轴之比对其抗剪强度的影响，但在相同相对密度下的研究并不多见．通过控制颗粒摩擦因数形成具有相同相对密度的试样，研究了0%、35%、65%及100%相对密度下颗粒的长短轴之比对试样抗剪强度的影响规律．另外，还进行了相同孔隙率下的试验以进行结果对比．研究结果表明，相同相对密度下，峰值状态和临界状态时试样剪应力随长短轴之比增大而增大，与相同孔隙率下的结果一致，但峰值剪应力增大幅值要比相同孔隙率下的小．另外，对不同长短轴之比下试样内摩擦角进行分析，发现临界状态时内摩擦角随长短轴之比增大而增大，而峰值状态时内摩擦角受长短轴之比的影响相对较小．最后从试样剪胀性方面进行了分析，阐述了以上现象发生的机理．

杆状颗粒；长短轴之比；相对密度；直剪试验；离散元法；剪胀性

0 引 言

自然界和现代工业中经常遇到各种形状的颗粒，例如生物材料和药品生产中常见的杆状和扁平状颗粒、岩土工程中常见的表面被风化腐蚀且带棱角的角砾、烧结工业中常见的非凸面体颗粒．研究表明颗粒形状是影响散粒材料力学行为的重要因素[1-3]．常规试验方法和测试手段只能从宏观层面定性研究颗粒形状对散粒材料力学行为的影响，无法探明散粒材料在颗粒层面上的细观力学本质．近年来离散元法的发展，使通过数值分析方法从细观层面分析颗粒形状对散粒材料宏观力学行为的影响成为可能．在离散元中几种典型的非球形颗粒包括多边形颗粒、椭圆形颗粒、杆状颗粒以及基于CT扫描而生成的非规则颗粒．

杆状颗粒几何形式简单，不会出现多边形颗粒构成时可能出现的奇异点，而且较基于CT扫描生成的非规则颗粒所需的计算量小．杆状颗粒本身其形状接近许多真实颗粒的形状(例如砾石、药片以及谷物等)，其形状特征主要用长短轴之比来进行表征，许多学者利用离散元法研究了长短轴之比对其力学行为的影响[4-8]．在以前的离散元数值模拟中存在两种比较方式，一种是通过控制试样处于相同孔隙率下进行对比，另一种是通过控制试样处于相同密度下进行对比，此处的密度即工程中经常使用的相对密度的概念．两种比较方式的结果可能不同，例如Ng[9]研究了相同孔隙率下椭球的长短轴之比对散粒材料宏观力学行为的影响，发现随着长短轴之比的增大，试样的峰值强度有逐渐减小的趋势；而在相同相对密度下，Rothenburg等[10]通过双轴试验发现试样的峰值强度随着长短轴之比增大而呈现单峰特性(即先增大后减小)．针对长短轴之比对杆状颗粒材料宏观力学的影响，有学者[5,8]研究表明相同孔隙率下，试样的峰值剪应力随长短轴之比的增大而增大，而相同相对密度下长短轴之比对杆状颗粒材料宏观力学行为影响的研究并不多见．

在离散元数值模拟中，密度的概念很少提及，主要是由于自然界中的真实颗粒形状以及级配曲线很难在数值试验中模拟．针对这一情况，Deluzarche 等[11]建议在离散元数值模拟中，以摩擦因数fc为标准来获取试样的最大、最小孔隙率，认为当fc=0时，试样的孔隙率最小．Abbireddy等[12]通过堆积试验，也得到了相同的结论．试样的实际摩擦因数对应的孔隙率为最大孔隙率，实际摩擦因数需要通过数值模拟与室内试验结果进行对比标定．以往在相同相对密度下的研究，都是在最密实状态下进行的，而在其他相对密度下的研究尚未见发表．

本文采用离散元计算程序(PFC3D)，利用clump模拟具有不同长短轴之比的杆状颗粒，尝试在数值直剪试验中使长短轴之比不同的杆状颗粒试样处于相同相对密度下，进而研究长短轴之比对杆状颗粒材料宏观力学行为的影响．主要分析峰值状态和临界状态时试样的抗剪强度受长短轴之比影响的变化趋势，通过分析试样的剪胀性进而阐明这种影响的机制．

1 数值模型

1.1 模型说明

尽管离散元法从细观层面揭示散粒材料的宏观物理力学行为有其独特优势，但受计算效率的制约，它很难在较大规模的计算中得到应用．在过去的研究中，针对准静态剪切问题，有学者通过不同的方法来增大临界时间步长来提高计算效率．经常采用的3种提高计算效率的方法有：(1)保持模型尺寸不变，增大颗粒的密度[13]；(2)减小颗粒间的接触刚度[14]；(3)保持颗粒的密度不变，增大颗粒的尺寸[15]．为了提高计算效率，本文采用了第3种方法，即增大颗粒的尺寸进行数值计算．

为了消除边界效应的影响，当颗粒尺寸增大时，模型箱的尺寸也相应增大．文中模型箱的长、宽、高分别为10、4和5 m，如图1所示．图1中两侧翼墙的作用是防止剪切过程中发生颗粒泄漏．Feng等[16]的研究表明采用颗粒和试样尺寸扩大法得到的计算结果也适用于小尺寸下的应力特性．施加于直剪盒顶部的竖向应力是通过顶部墙体施加的，同时利用伺服控制保证在剪切过程中竖向应力不变．在剪切过程中，给定下部墙体5 mm/s 的速度来模拟直剪过程．监测发现，系统的平均不平衡力与平均接触力之比为10-5量级，说明此剪切速度满足准静态剪切的标准[17]．在剪切过程中，通过记录下部墙体的水平位移与试样的初始高度之比得到剪切应变．剪切应力根据下部剪切盒左右墙体的沿水平方向合力与试样的横截面计算，其表达式如式(1)所示[18]：

(1)

式中：Fs为下部剪切盒墙体沿水平方向的合力，W为直剪盒宽度，L为直剪盒长度，v为剪切速率，t为已剪切时间．

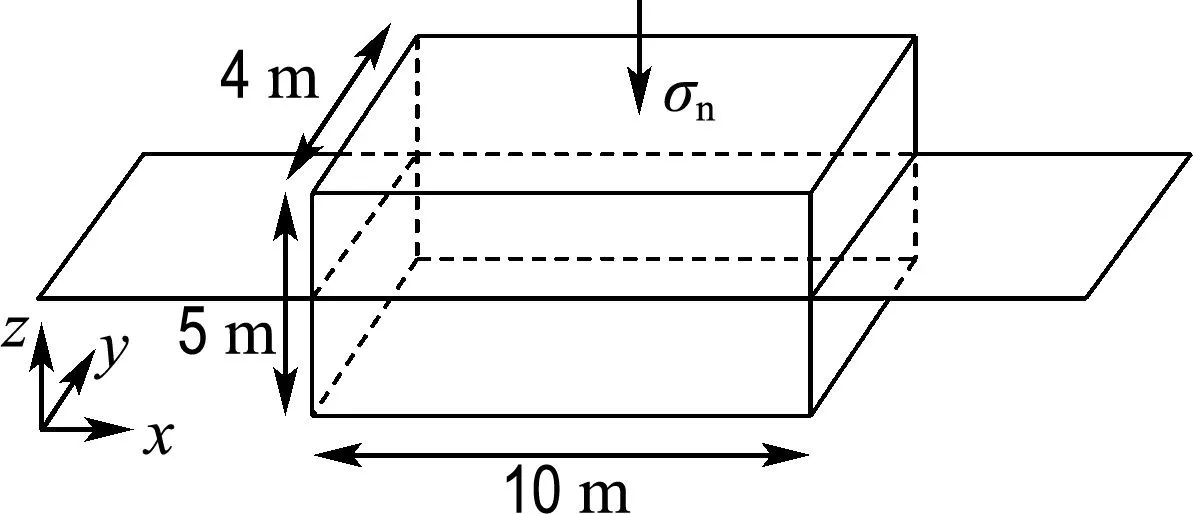
图1 直剪盒示意图

1.2 模型建立

针对杆状颗粒，一般采用长短轴之比R来对颗粒形状进行描述(R=a/b，其中a、b分别代表颗粒的长轴和短轴)．以往的数值模拟中，采用的R集中在1～2，这与常见的颗粒的长短轴之比集中在这个范围内相关，例如Stahl等[19]测量一种天然砾石土，发现其长短轴之比小于2的颗粒约占90%．本文采用的杆状颗粒的R均在1～2，图2为本文采用的5种不同的杆状颗粒，R分别为1.00、1.25、1.50、1.75和2.00．为了消除颗粒级配对宏观力学行为的影响，本文颗粒级配采用均一粒径．

图2 不同形状的颗粒

试样通过落雨法生成．首先在位于模型箱顶部4 m高处生成特定形状的颗粒．在颗粒开始下落前，给定颗粒不同的摩擦因数，然后让其在重力作用下自由堆积．当试样达到平衡后，测定各试样的孔隙率．图3给出了孔隙率与摩擦因数之间的关系．从图中可以看出，当摩擦因数小于0.5时，相同摩擦因数对应的不同形状颗粒组成试样的孔隙率往往不同，R=1.25与R=1.50试样对应的孔隙率大小接近，并较其他试样的孔隙率小，这与Guises等[20]测定的R=1.50椭球对应孔隙率最小趋势一致．当摩擦因数大于0.5时，孔隙率随摩擦因数的增大而基本保持不变．

图3 不同形状颗粒组成试样孔隙率与摩擦因数的对应关系

Fig.3 The relationship between porosity of assembly composed of different particle shapes and their friction factor

为了合理判定散粒材料的密度状态，工程中经常使用相对密度Dr的概念．Dr的表达式为[21]

(2)

其中nmin、nmax、n分别表示试样的最小、最大以及当前的孔隙率．Deluzarche等[11]建议在离散元数值模拟中，以颗粒的摩擦因数fc为标准来获取试样的最大、最小孔隙率．当fc=0时，试样处于最密实状态(此时孔隙率为nmin)，试样的实际摩擦因数对应的孔隙率为最大孔隙率(此时孔隙率为nmax)．许多学者通过数值试验[11,21]表明通过上述方法获得的相对密度与真实散粒材料的相对密度具有相似的受力变形特点．本文假定试样的实际摩擦因数为0.5，因此认为fc=0.5对应的孔隙率为最大孔隙率．通过控制试样堆积过程中的摩擦因数，使不同长短轴之比的试样处于相同相对密度下，进而研究长短轴之比对杆状颗粒材料剪切行为的影响，共研究了0%、35%、65%及100% 4种情况．基于式(2)，在离散元模型中通过控制颗粒摩擦因数的方法获得不同相对密度的试样是合理的，而在实际的室内试验中往往是通过控制试样体积，击实试样的方法来达到预定相对密度．当Dr、nmin、nmax已知时，根据式(2)可以求出对应的孔隙率n．对于某一特定长短轴之比的试样，当已知孔隙率n时，结合图3中n-fc的对应关系，可得到生成该孔隙率对应的颗粒摩擦因数fc．表1给出了5种颗粒形状试样在4种不同相对密度下的孔隙率及形成该孔隙率对应的摩擦因数fc．另外，为了与相同孔隙率下长短轴之比对杆状颗粒材料抗剪强度的影响结果进行对比，还进行了相同孔隙率下(n=0.42)的剪切试验．对于R=1.00、1.25、1.50、1.75及2.00，当n=0.42时，根据式(2)，其Dr分别为31%、0%、18%、36%及100%．

表1 不同相对密度试样的孔隙率及生成该试样的摩擦因数

Tab.1 The porosity of assembly with different relative densities and friction factor to form the corresponding assembly

RDr=0%Dr=35%Dr=65%Dr=100%nmaxfcnfcnfcnminfc1.000.440.50.420.190.390.100.3701.250.420.50.380.170.350.070.3001.500.440.50.400.250.360.100.3101.750.460.50.420.240.390.090.3402.000.530.50.500.240.470.080.420

由于采用颗粒尺寸扩大法，相较于室内直剪试验，施加于直剪盒顶部的竖向应力也应相应增大．为了使施加于数值试验与室内试验直剪盒顶部的竖向应力具有可比性，Cui等[22]建议利用一个量纲一的参数σn/(Ws/r2)来进行分析，其中σn为竖向应力(如图1所示)，Ws为单个颗粒的平均重力，r为颗粒的半径．在室内试验中，一般建议施加的竖向应力满足σn/(Ws/r2)在100～1 000．本文采用10 MPa作为施加于直剪盒顶部的竖向应力，对应的σn/(Ws/r2)=450，位于室内试验所建议的范围之内．

数值试验中采用的参数如表2所示．采用线性接触模型来模拟颗粒之间及颗粒与墙体之间的相互作用，颗粒的法向刚度kn采用式(3)确定：

kn=2Ecd

(3)

式中：d为相接触颗粒直径的较小值，Ec为弹性模量．切向刚度ks取与kn相同值．表2中参数主要借鉴Gu等[23]数值试验的取值．数值试验中墙体与颗粒间的摩擦往往会影响试样的抗剪强度，为了忽略这种影响，将墙体的摩擦因数设置为0．另外文中主要研究对象为散粒材料，因此颗粒间的黏聚力为0，且颗粒间的滑动满足库仑摩擦定律．

表2 数值试验中采用的参数

2 数值模拟结果

2.1 相同孔隙率下的模拟结果

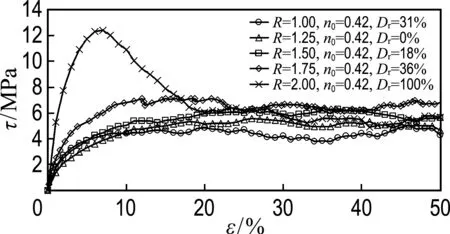
图4给出了5种不同长短轴之比试样在相同初始孔隙率(n0=0.42)下数值模拟结果，包括图4(a)中的剪应力-剪应变及图4(b)中的孔隙率-剪应变关系曲线．从图中可以看出，相同初始孔隙率下试样的剪应力-剪应变及孔隙率-剪应变呈现出不同的特点．对于R=1.00、1.25、1.50和1.75试样，由于处于相对疏松状态，应力应变呈现出硬化特点，对应孔隙率随剪应变增大逐渐减小直至临界状态．对于R=2.00试样，由于Dr=100%，试样处于最密实状态，剪应力在达到峰值后呈现出应变软化特点，R=2.00试样对应的孔隙率随剪应变增大而逐渐增大直到临界状态．

(a) 剪应力与剪应变关系曲线

(b) 孔隙率与剪应变关系曲线

图4 相同初始孔隙率、不同长短轴之比试样的剪应力、孔隙率与剪应变的关系曲线

Fig.4 The curves of shear stress and porosity against shear strain of assemblies with different aspect ratios and same initial porosity

从图4(a)中可以看出，在相同孔隙率下，试样的峰值剪应力随长短轴之比增大而增大，这一趋势与Ting等[1]和Yan[5,8]数值模拟的结果一致．根据库仑摩擦定律，散粒材料(黏聚力c=0)在直剪试验中的库仑摩擦角可表示为

tanφc=τs/σn

(4)

图4(a)的结果显示R=1.00试样在达到临界状态(剪应变大于20%)时剪应力达到峰值，而R=2.00试样在剪应变约为7%时达到峰值．根据式(4)，R=1.00和R=2.00试样达到峰值时的φc分别为23.8°和51.4°，增幅为27.6°．Taylor[24]认为试样的抗剪强度由颗粒间的摩擦和咬合作用提供，文中颗粒间的摩擦因数相同，随着相对密度的增大，颗粒间的咬合作用逐渐增大，因此试样的峰值强度逐渐增大．

2.2 相同相对密度下的模拟结果

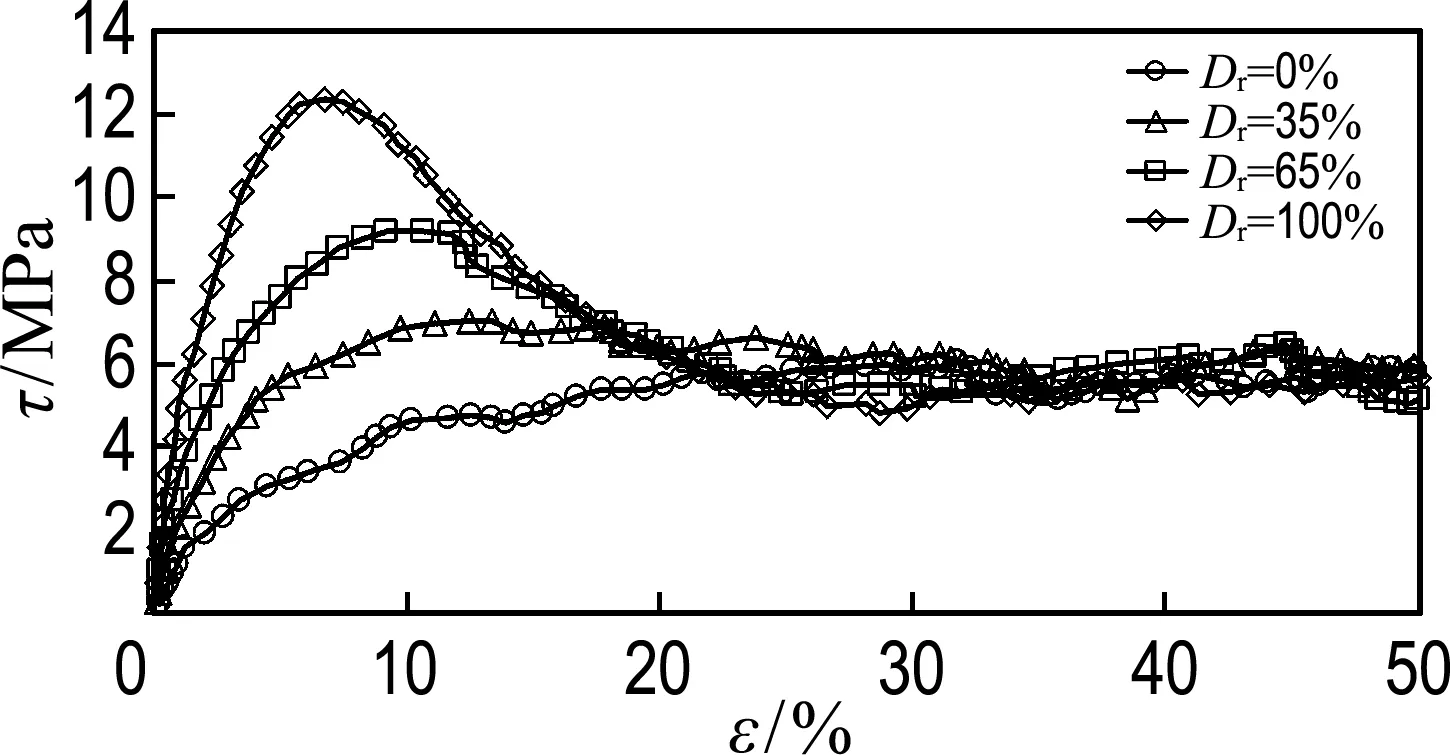
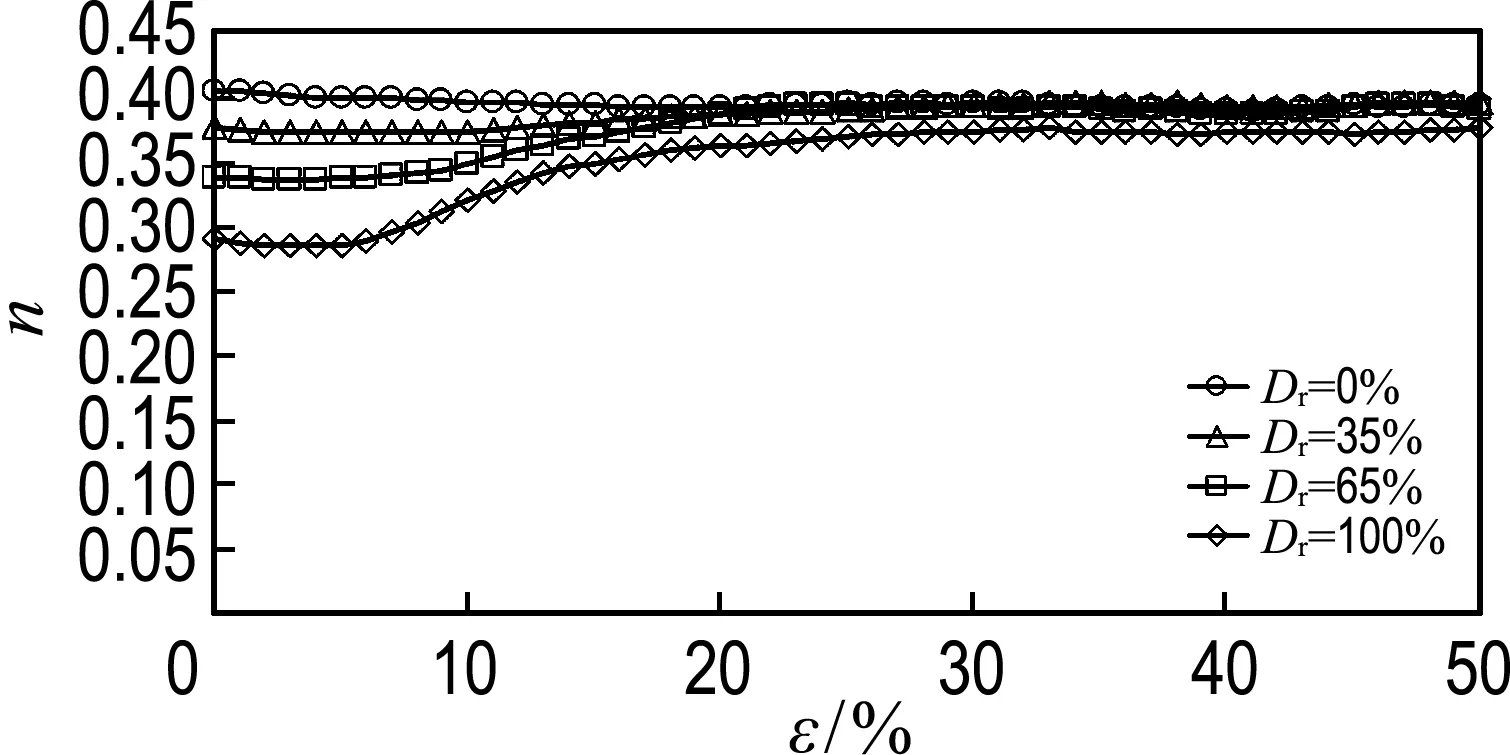
以R=1.50为例，图5给出了其在不同相对密度下的剪应力-剪应变和孔隙率-剪应变的关系曲线．从图中可以看出，R=1.50试样在不同相对密度下表现出不同的剪切特性．在较低相对密度(Dr为0%和35%)下，图5(a)显示试样的剪应力随剪应变逐渐增大呈现应变硬化，对应图5(b)中的孔隙率随剪应变增大而逐渐减小直到临界孔隙率．当相对密度较高(Dr为65%和100%)时，图5(a) 显示试样峰值后剪应力随剪应变增大而降低，呈现应变软化特点，对应图5(b)中的孔隙率随剪应变增大而增大直到临界孔隙率．随相对密度的增大，试样的峰值剪应力逐渐增大，残余强度和孔隙率在剪应变达到20%时逐渐趋于一致．以上关系曲线与典型的砂土室内直剪试验结果[25]一致，说明在离散元数值模拟中利用相对密度的概念能正确重现散粒材料在真实物理模型中的剪切行为特征．

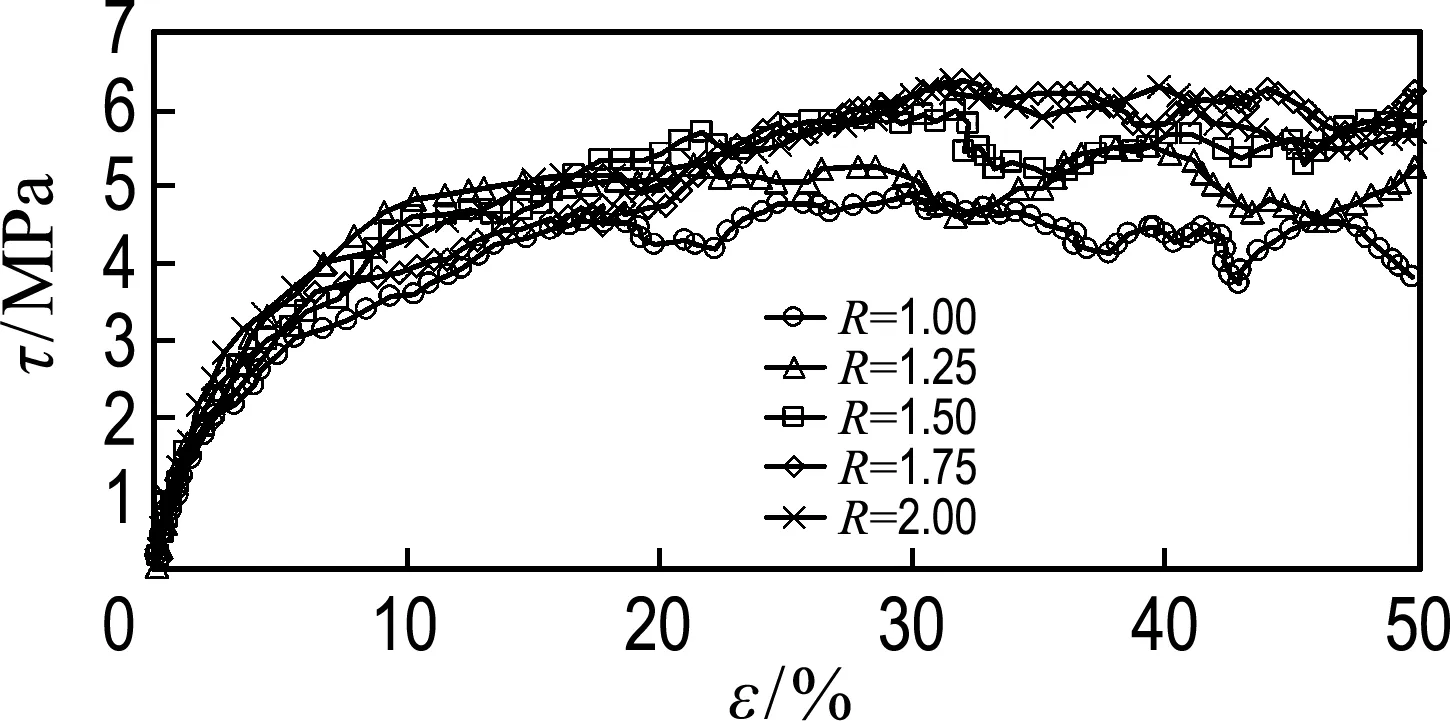
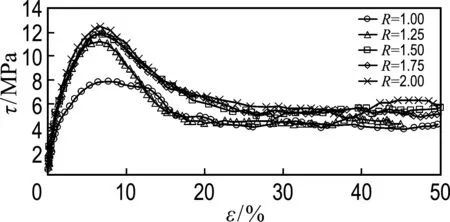
图6给出了Dr为0%和100%下各试样的剪应力-剪应变关系曲线，Dr=35%和Dr=65%曲线趋势与Dr=100%相似．图5(a)显示当试样处于临界状态时，其剪切强度与初始状态无关，以往研究长短轴之比对试样抗剪强度的影响常在临界状态时进行对比分析．从图6(a)和(b)中可以看出，各相对密度下的试样达到临界状态后，试样的残余强度随长短轴之比增大而增大，与文献[4,7]的趋势一致．根据式(4)，图7中给出了不同相对密度下非球形颗粒的峰值状态与临界状态时对应的tanφc与R的关系，其中实心符号表示峰值状态时的tanφc，空心符号表示临界状态时的tanφc．当试样达到临界状态时，R=1.00试样对应φc为20.8°，R=2.00试样对应φc为26.2°，增幅为5.4°．

(a) 剪应力与剪应变关系曲线

(b) 孔隙率与剪应变关系曲线

图5R=1.50、不同相对密度下的剪应力、孔隙率与剪应变的关系曲线

Fig.5 The curves of shear stress and porosity against shear strain for R=1.50 with different relative densities

试样的峰值强度能反映材料的极限承载能力，因此是工程上重点关注的参数之一．由于本文中球形颗粒并未考虑滚动摩擦作用，图6(b)中球形颗粒试样的峰值强度小于非球形颗粒的峰值强度．对于非球形颗粒，从图7中可以看出，随长短轴之比增大，峰值库仑摩擦角有较小幅值的增大．Dr=100%时，当试样剪应力达到峰值时，R=1.25 试样对应φc为48.2°，R=2.00试样对应φc为51.4°，增幅为3.2°．对比相同孔隙率下的结果可以发现，相同相对密度下，随着长短轴之比增大，峰值强度和残余强度也逐渐增大，但增幅明显小于相同孔隙率下的结果．

(a) Dr=0%

(b)Dr=100%

图6 相同相对密度下剪应力与剪应变关系曲线

Fig.6 The curves of shear stress against shear strain with constant relative density

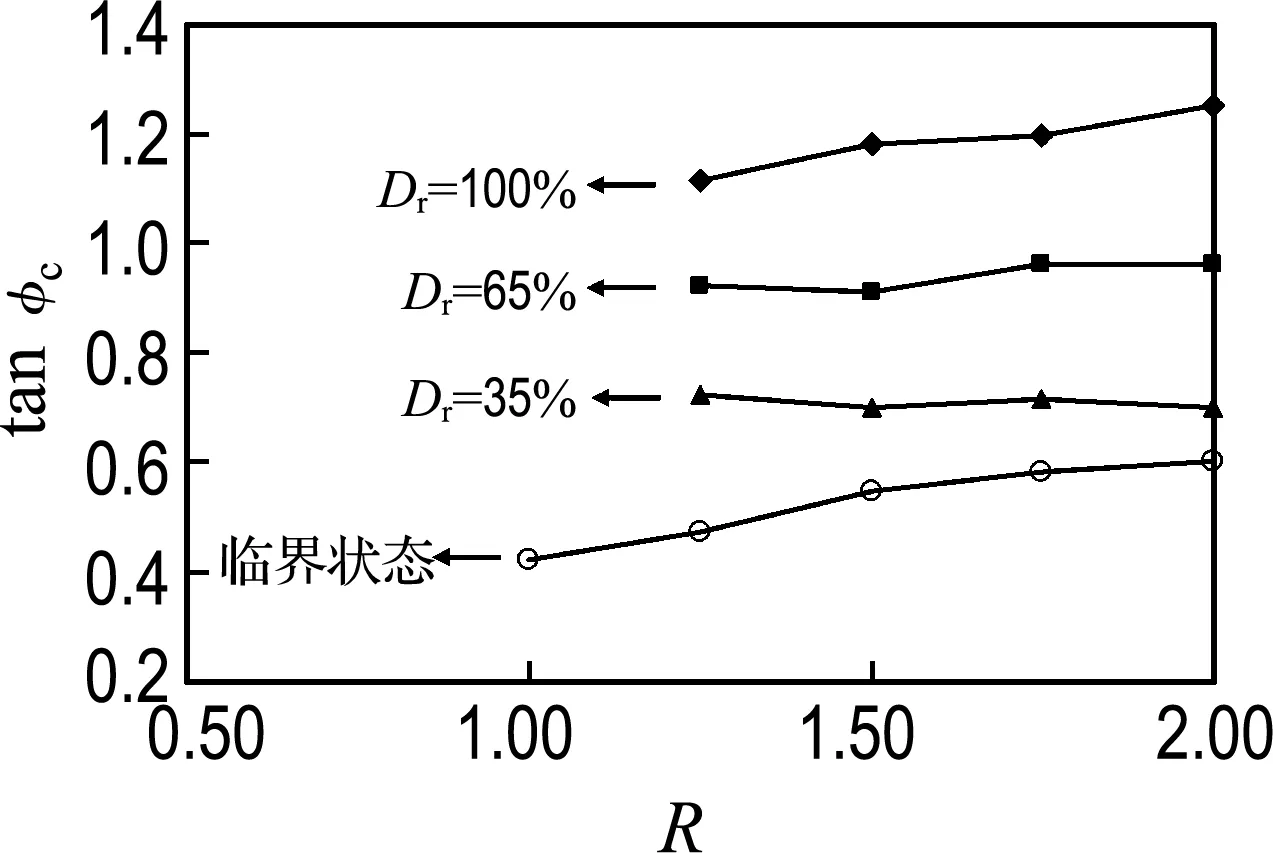
图7 不同相对密度下试样在剪应力达到峰值和临界状态时的tanφc与长短轴之比的关系

Fig.7 The relationship between tan φc(at peak state and critical state) and aspect ratio with different relative densities

2.3 相同相对密度下的内摩擦角

直剪试验中当剪应力达到峰值时，Oda等[26]认为此时主应力方向与主应变增量方向同轴．根据同轴假定，此时直剪盒内的应力状态可以用摩尔圆来表示，如图8所示[27]．

根据摩尔-库仑破坏准则，材料的内摩擦角可表示为

(5)

其中φm为根据摩尔-库仑破坏准则得到的内摩擦角，σ1、σ3为试样的最大、最小主应力，σn为直剪盒顶部的竖向应力．直剪试验中，由于破坏面为固定面，不能真实反映材料的强度，数值试验中也常采用φm来评价散粒材料的剪切强度．实际上，根据图8中的几何关系，剪应力达到峰值时tanφc和sinφm有如下关系：

(6)

式中：ψ为试样的剪胀角；φc为假定剪切面为一平面，通过受力分析而得到的库仑摩擦角(式(4))；φm为根据试样内部的主应力而计算得到的内摩擦角(式(5))．在离散元中，可根据下式[28]计算试样各方向的应力值：

(7)

式中：Nc为试样内所有clump的实际接触数目，c0为某个特定的接触，fi为对应接触c0在i方向的接触力，dj为两接触clump的形心连线在j方向的长度，V为试样的总体积．求得各方向的应力值后，主应力与σij间有如下关系：

(8)

其中I1、I2、I3分别为第一、第二、第三应力不变量．以R=1.25为例，图9给出了σ1/σn和σ3/σn与剪应变的关系曲线，其他颗粒形状试样的变化趋势与图9相似．从图中可以看出，σ1/σn的峰值随着相对密度的增大而增大，当剪应变趋近20%时，σ1/σn逐渐达到临界状态．随着剪应变增大，σ3/σn先减小后增大，当σ1/σn达到峰值时，σ3/σn同时达到最小值，且σ3/σn的最小值随相对密度的增大而减小．

图8 直剪试验中试样的应力摩尔圆[27]

对比图5和9结果可以发现当剪应力达到峰值和临界状态时，试样最大、最小主应力也刚好达到峰值和临界状态．将图9中主应力达到峰值和临界状态时的值代入式(5)可求得对应的sinφm．

图9R=1.25、不同相对密度下的σ1/σn和σ3/σn与剪应变的关系曲线(实心符号表示σ1/σn，空心符号表示σ3/σn)

Fig.9 The curves of σ1/σnand σ3/σnagainst shear strain for R= 1.25 with different relative densities (the solid mark indicates σ1/σn, the hollow mark indicates σ3/σn)

当试样处于最密实状态时，Azéma等[7]利用数值双轴试验研究了长短轴之比对杆状颗粒试样抗剪强度的影响．为了与其结果进行对比，图10中给出了不同相对密度下试样在峰值与临界状态时的sinφm与R的关系，其中实心符号表示峰值状态对应的sinφm，空心符号表示本文以及文献[7]在临界状态对应的sinφm．

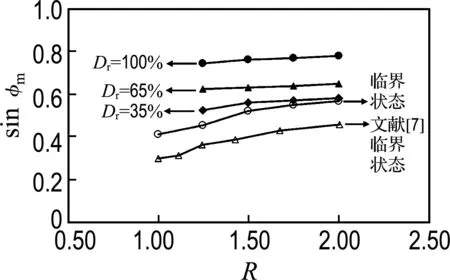
图10 不同相对密度下试样在峰值和临界状态时的sinφm与长短轴之比的关系

Fig.10 The relationship between sin φm(at peak state and critical state) and aspect ratio with different relative densities

由于临界状态时剪胀角为0，根据式(6)有tanφc=sinφm，因此图10中的sinφm实际等于图7中各试样达到临界状态时的tanφc．从图10中可以看出，试样达到临界状态时的sinφm随R增大而增大，其趋势与文献[7]的趋势相同．当R分别为1.00和2.00，试样达到临界状态时的φm分别约为22.3°和29.5°，其增幅为7.2°，略小于文献[7]中对应增幅(约为9.8°)，大于前文得到的临界状态时对应φc的增幅(5.4°)．另外，从图10中也可以看出，对比临界状态时sinφm与R的关系可以发现，试样剪应力达到峰值时对应的sinφm随R的增大而增大，但其增大幅值比临界状态时的小，Nouguier-Lehon[6]通过数值双轴试验也观察到了类似现象．

3 数值模拟结果分析

Bolton[29]基于大量砂土直剪试验，提出了以下经验公式：

φp=φcrit+0.8ψp

(9)

其中φp和φcrit分别为试样剪应力达到峰值和临界状态时对应的内摩擦角，ψp为试样剪应力峰值时对应的剪胀角．Guo等[30]、戴北冰等[31]考虑砂土颗粒破碎、级配以及颗粒尺寸的大小，提出了更一般的公式：

φp=φcrit+kψp

(10)

其中k为考虑以上因素时的状态参数．三维直剪试验中剪胀角可根据下式求得[32]：

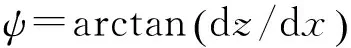
(11)

其中dz和dx分别为试样在z方向、x方向的增量位移，坐标轴方向如图1所示．直剪试验过程中，剪应变每增大0.05%时记录一次顶部墙体的竖向位移和底部直剪盒的水平位移，将记录的数值依据式(11)求得特定剪应变下的剪胀角[33]．

以R=1.25为例，根据式(11)，图11给出了不同相对密度下的剪胀角随剪应变的关系曲线，其他试样的剪胀角随剪应变的变化趋势与图11中相似．从图中可以看出，随着相对密度的增大，剪胀角逐渐增大．当剪应变达到20%时，不同相

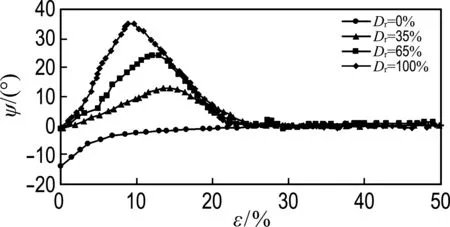
图11R=1.25、不同相对密度下的剪胀角与剪应变的关系曲线

Fig.11 The curves of the angle of dilatancy against shear strain for R=1.25 with different relative densities

对密度的试样逐渐达到临界状态，此时剪胀角为零．值得注意的是，一般密实砂土的剪胀角小于20°,而图11中试样在Dr=100%时剪胀角达到34.5°，这主要与本文采用颗粒扩大法有关．当颗粒尺寸增大时，试样的剪胀性随之增大，图12给出了其原理示意图．

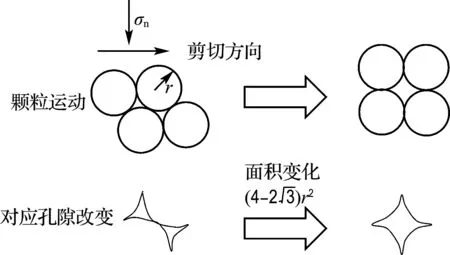
图12 颗粒大小对剪胀性的影响[26]

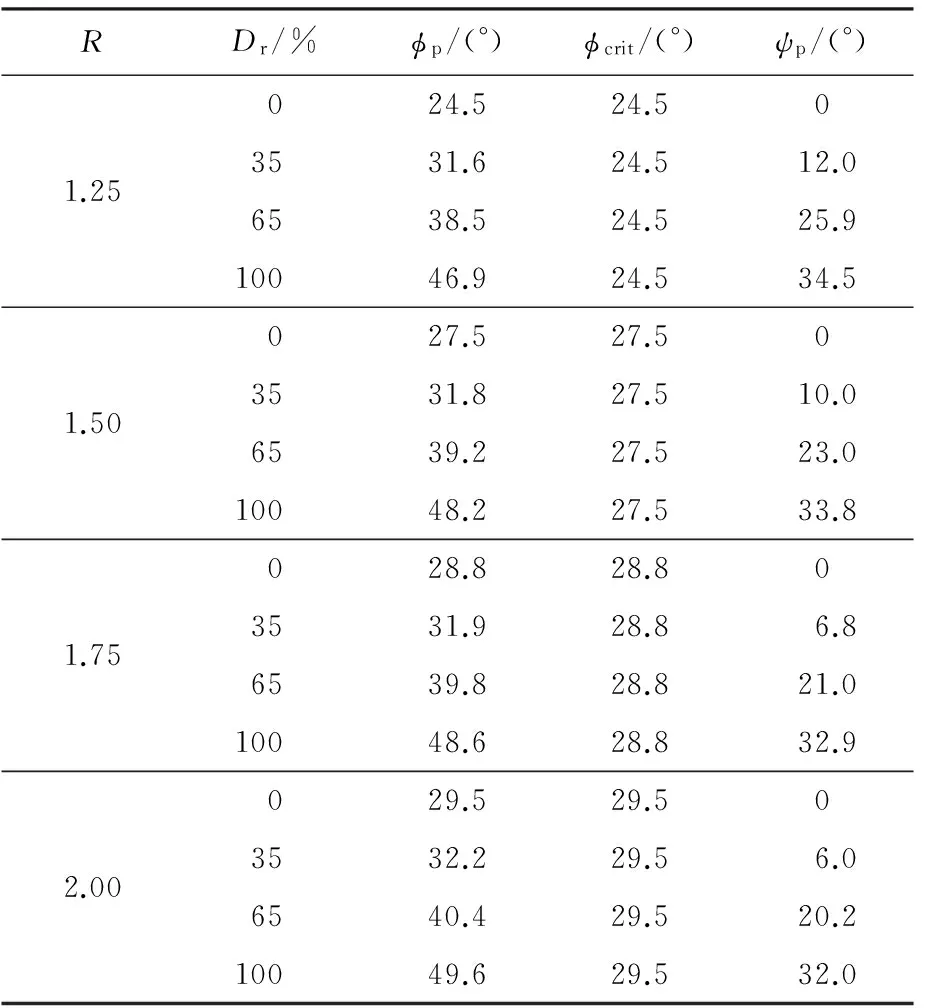
室内试验和数值模拟中经常会采用颗粒级配替代法，即用较大尺寸的颗粒来替代较小尺寸的颗粒以方便试验．本文的研究表明，这样处理会对试样的剪胀性和剪切强度造成一定影响．限于篇幅，不在此对颗粒级配替代法做深入探讨．表3给出了非球形颗粒试样在不同相对密度下的φp、φcrit和ψp．

表3 非球形颗粒试样在不同相对密度下的φp、φcrit和ψp

Tab.3 The φp,φcritand ψpof assembly with non-spherical particles at different relative densities

RDr/%ϕp/(°)ϕcrit/(°)ψp/(°)1.25024.524.503531.624.512.06538.524.525.910046.924.534.51.50027.527.503531.827.510.06539.227.523.010048.227.533.81.75028.828.803531.928.86.86539.828.821.010048.628.832.92.00029.529.503532.229.56.06540.429.520.210049.629.532.0

基于表3的数据，图13给出了不同相对密度下φp-φcrit与ψp间的关系，从图中可以看出，两者间符合较好的线性关系：

φp-φcrit=0.589ψp

(12)

以上关系说明，对于本文的杆状颗粒，不同相对密度下试样的状态参数k可以用相同值表示．注意由于本文采用clump模拟颗粒形状，没有考虑颗粒破碎的影响，Guo等[30]研究发现不同形状颗粒考虑破碎情况时，状态参数一般会发生改变．本文基于杆状颗粒得到的状态参数为0.589，与Guo等[30]研究得到的表面圆滑的砂颗粒的状态参数(k=0.63)相近,说明杆状颗粒的剪应力-剪胀行为相似于表面圆滑的砂．另外，从表3中可知，相同Dr下，ψp随R增大而减小．根据式(10)，由于φcrit和ψp随R增大的变化趋势相反，而状态参数k对不同长短轴之比的试样可视为常数(k=0.589)，因此试样剪应力达到峰值时，φp受R的影响相对较小．

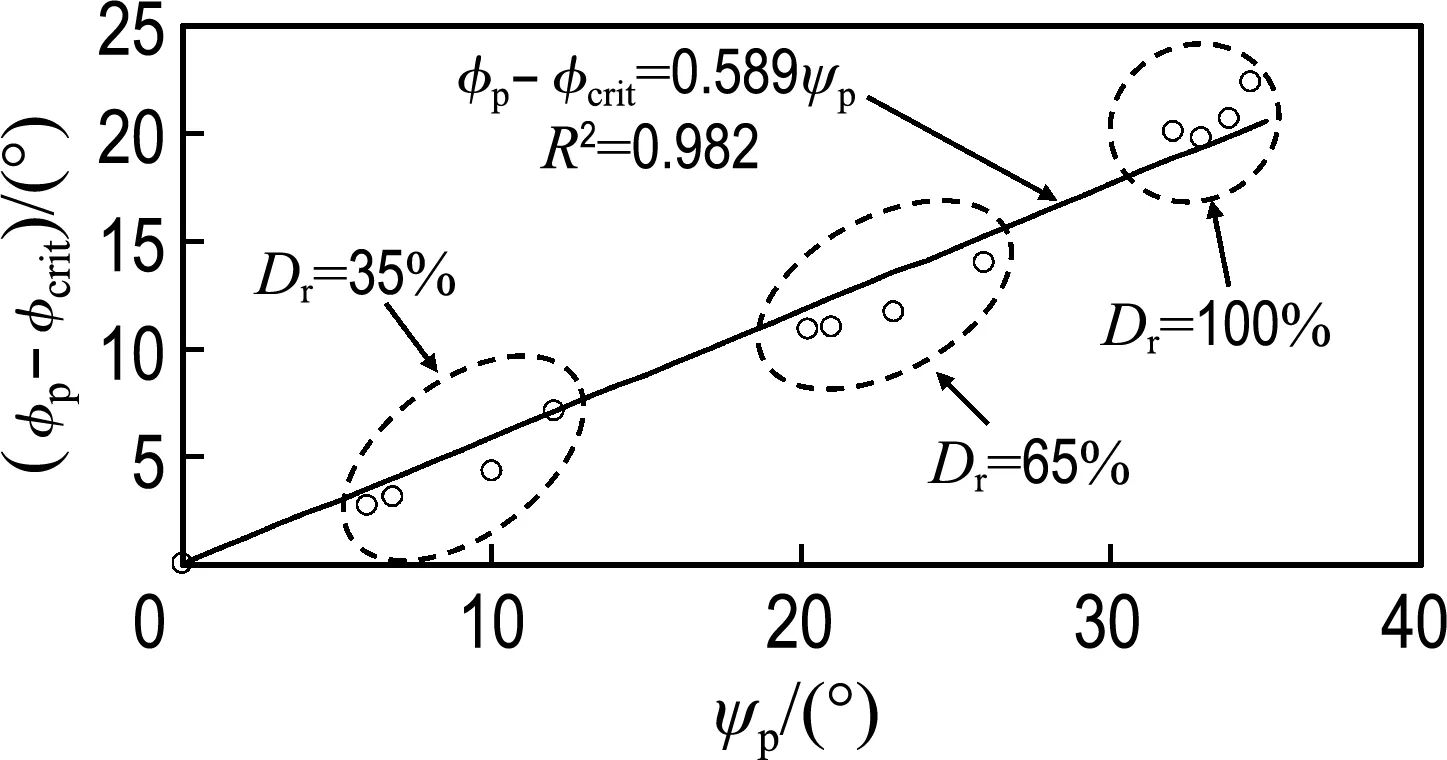
图13 不同相对密度下试样的φp-φcrit与ψp的关系

Fig.13 The relationship between φp-φcritand ψpwith different relative densities

4 结 论

(1) 相同孔隙率下，试样的峰值剪应力随长短轴之比的增大而增大，R从1.00到2.00，φc增幅为27.6°．相同相对密度下，试样达到临界状态时对应抗剪强度随长短轴之比的增大而增大，临界状态时R从1.00到2.00， φc增幅为5.4°，剪应力达到峰值时，φc随长短轴之比增大而增大，但增大幅值相对较小．对比相同孔隙率下的结果可以发现，相同相对密度下，随着长短轴之比增大，峰值强度和残余强度增幅明显小于相同孔隙率下的结果，这主要是由不同相对密度下咬合作用不同引起的．

(2)对试样剪应力达到峰值和临界状态时的内摩擦角(φm)也做了分析．试样处于临界状态时，R=1.00和R=2.00对应φm分别为22.3°和29.5°，增幅为7.2°．剪应力达到峰值时，φm随长短轴之比增大而增大，但增大幅值相对较小．

(3)最后分析了试样的剪胀性，发现φp-φcrit与ψp之间满足较好的线性关系，其中斜率表示状态参数，k为0.589，较典型砂土的状态参数小，与表面圆滑的砂的状态参数相近(k=0.63)，说明杆状颗粒的剪应力-剪胀行为更相似于表面圆滑的砂．另外，发现在相同相对密度下，试样的峰值剪胀角随长短轴之比的增大而逐渐减小，而φcrit随长短轴之比增大的趋势与其相反．根据φp=φcrit+kψp，φp较φcrit受长短轴之比增大的影响相对较小．

[1]TingJM,MeachumL,RowellJD.Effectofparticleshapeonthestrengthanddeformationmechanismsofellipse-shapedgranularassemblages[J].EngineeringComputations, 1995, 12(2):99-108.

[2]ShinoharaK,OidaM,GolmanB.Effectofparticleshapeonangleofinternalfrictionbytriaxialcompressiontest[J].PowderTechnology, 2000, 107(1-2):131-136.

[3]AntonySJ,KuhnMR.Influenceofparticleshapeongranularcontactsignaturesandshearstrength:Newinsightsfromsimulations[J].InternationalJournalofSolidsandStructures, 2004, 41(21):5863-5870.

[4]Nouguier-LehonC,CambouB,VincensE.Influenceofparticleshapeandangularityonthebehaviourofgranularmaterials:Anumericalanalysis[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2003, 27(14):1207-1226.

[5]YanWM.Fabricevolutioninanumericaldirectsheartest[J].ComputersandGeotechnics, 2009, 36(4):597-603.

[6]Nouguier-LehonC.Effectofthegrainelongationonthebehaviourofgranularmaterialsinbiaxialcompression[J].ComptesRendusMecanique, 2010, 338(10):587-595.

[7]AzémaE,RadjaïF.Stress-strainbehaviorandgeometricalpropertiesofpackingsofelongatedparticles[J].PhysicalReviewE-Statistical,Nonlinear,andSoftMatterPhysics, 2010, 81(5):051304.

[8]YanWM.Particleelongationanddepositioneffecttomacroscopicandmicroscopicresponsesofnumericaldirectsheartests[J].GeotechnicalTestingJournal, 2011, 34(3):238-249.

[9]NgT.Particleshapeeffectonmacro-andmicro-behaviorsofmonodisperseellipsoids[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2009, 33(4):511-527.

[10]RothenburgL,BathurstRJ.Micromechanicalfeaturesofgranularassemblieswithplanarellipticalparticles[J].Geotechnique, 1992, 42(1):79-95.

[11]DeluzarcheR,CambouB.Discretenumericalmodellingofrockfilldams[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomechanics, 2006, 30(11):1075-1096.

[12]AbbireddyCOR,ClaytonCRI.VaryinginitialvoidratiosforDEMsimulations[J].Geotechnique, 2010, 60(6):497-502.

[13]ThorntonC.Numericalsimulationsofdeviatoricsheardeformationofgranularmedia[J].Geotechnique, 2000, 50(1):43-53.

[14]HärtlJ,OoiJY.Experimentsandsimulationsofdirectsheartests:Porosity,contactfrictionandbulkfriction[J].GranularMatter, 2008, 10(4):263-271.

[15]JacobsonDE,ValdesJR,EvansTM.Anumericalviewintodirectshearspecimensizeeffects[J].GeotechnicalTestingJournal, 2007, 30(6):512-516.

[16]FengYT,OwenDRJ.Discreteelementmodellingoflargescaleparticlesystems—I:exactscalinglaws[J].ComputationalParticleMechanics, 2014, 1(2):159-168.

[17]MassonS,MartinezJ.Micromechanicalanalysisoftheshearbehaviorofagranularmaterial[J].JournalofEngineeringMechanics, 2001, 127(10):1007-1016.

[18] 赵金凤,严 颖,季顺迎. 基于离散元模型的土石混合体直剪试验分析[J]. 固体力学学报, 2014, 35(2):124-134.

ZHAOJin-feng,YANYing,JIShun-ying.Analysisofdirectsheartestofsoil-rockmixturebasedondiscreteelementmodel[J].ChineseJournalofSolidMechanics, 2014, 35(2):124-134. (inChinese)

[19]StahlM,KonietzkyH.Discreteelementsimulationofballastandgravelunderspecialconsiderationofgrain-shape,grain-sizeandrelativedensity[J].GranularMatter, 2011, 13(4):417-428.

[20]GuisesR,XiangJ,LathamJ-P, et al.Granularpacking:Numericalsimulationandthecharacterisationoftheeffectofparticleshape[J].GranularMatter, 2009, 11(5):281-292.

[21]SalotC,GottelandP,VillardP.Influenceofrelativedensityongranularmaterialsbehavior:DEMsimulationsoftriaxialtests[J].GranularMatter, 2009, 11(4):221-236.

[22]CuiL,O′SullivanC.Exploringthemacro-andmicro-scaleresponseofanidealisedgranularmaterialinthedirectshearapparatus[J].Geotechnique, 2006, 56(7):455-468.

[23]GUXiao-qiang,HUANGMao-song,QIANJian-gu.DEMinvestigationontheevolutionofmicrostructureingranularsoilsundershearing[J].GranularMatter, 2014, 16(1):91-106.

[24]TaylorDW.FundamentalsofSoilMechanics[M].NewYork:JohnWileyandSonsInc., 1948.

[25]ParkLK,SuneelM,ChulIJ.ShearstrengthofJumunjinsandaccordingtorelativedensity[J].MarineGeoresources&Geotechnology, 2008, 26(2):101-110.

[26]OdaM,KonishiJ.Rotationofprincipalstressesingranularmaterialduringsimpleshear[J].SoilsandFoundations, 1974, 14(4):39-53.

[27]ZhangL,ThorntonC.Anumericalexaminationofthedirectsheartest[J].Geotechnique, 2007, 57(4):343-354.

[28]ChristoffersenJ,MehrabadiMM,Nemat-NasserS.Micromechanicaldescriptionofgranularmaterialbehavior[J].JournalofAppliedMechanics,TransactionsofASME, 1981, 48(2):339-344.

[29]BoltonMD.Strengthanddilatancyofsands[J].Geotechnique, 1986, 36(1):65-78.

[30]GuoP,SuX.Shearstrength,interparticlelocking,anddilatancyofgranularmaterials[J].CanadianGeotechnicalJournal, 2007, 44(5):579-591.

[31] 戴北冰,杨 峻,周翠英. 颗粒摩擦对颗粒材料剪切行为影响的试验研究[J]. 力学学报, 2013, 45(3):375-383.

DAIBei-bing,YANGJun,ZHOUCui-ying.Anexperimentalstudyontheeffectofinter-particlefrictiononshearbehaviorofgranularmaterials[J].ChineseJournalofTheoreticalandAppliedMechanics, 2013, 45(3):375-383. (inChinese)

[32]LIUSi-hong.SimulatingadirectshearboxtestbyDEM[J].CanadianGeotechnicalJournal, 2006, 43(2):155-168.

[33]GONGJian,LIUJun.Analysisonthemechanicalbehaviorsofsoil-rockmixturesusingdiscreteelementmethod[J].ProcediaEngineering, 2015, 102:1783-1792.

Analysis of effect of aspect ratio on shear strength of granular materials based on DEM

GONG Jian, LIU Jun*

( School of Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China )

The elongated particles have attracted much attention from academic interests because their particle shapes are similar to many real particles (e.g., gravels, pills and grains). The shape of elongated particles can be characterized by aspect ratio. Many researchers have studied the effect of aspect ratio on shear strength of elongated particles at a constant porosity based on discrete element method (DEM). However, the research on a constant relative density is limited. The effect of aspect ratio on shear strength of elongated particles is studied at 0%, 35%, 65% and 100% relative density. The constant relative density of assemblies is formed by adjusting the friction factor of particles. Alternatively, the numerically direct shear tests at a constant porosity are also conducted in order to compare the results with those at a constant relative density. The test results indicate that increased aspect ratio leads to increase of the shear stress at peak state and critical state at a constant relative density, and this trend is consistent with the result at a constant porosity. However, the increased value of peak shear stress at a constant relative density is much smaller than that at a constant porosity. Furthermore, the angles of internal friction of assemblies with different aspect ratios are analyzed. It is found that increased aspect ratio leads to increase of the angle of internal friction at critical state, whereas increased aspect ratio has relatively small influence on the angle of internal friction at peak state. The aforementioned phenomena are explained by analyzing the dilatancy of assemblies.

elongated particles; aspect ratio; relative density; direct shear tests; discrete element method (DEM); dilatancy

1000-8608(2016)02-0153-10

2015-09-01；

2016-01-11．

国家自然科学基金资助项目(51479027，51539008).

龚 健(1985-)，男，博士生，E-mail:gjdlut@mail.dlut.edu.cn；刘 君*(1972-)，男，博士，教授，E-mail:junliu@dlut.edu.cn.

TU47

A

10.7511/dllgxb201602007