非线性球形脉冲波在焦点的传播与干扰
2016-12-01袁明生
袁 明 生
( 上海对外经贸大学 商务信息学院, 上海 201620 )
非线性球形脉冲波在焦点的传播与干扰
袁 明 生*
( 上海对外经贸大学 商务信息学院, 上海 201620 )
在小初值的条件下,讨论了半线性波动方程组脉冲波解的性质,利用非线性几何光学的方法,证明非线性几何光学给出的解在焦点附近是有效的.描述了脉冲波的传播和干扰以及干扰后新脉冲波的产生情况.通过微分变换,利用球形对称性将波动方程组化为一阶双曲型方程,得到一阶近似解所满足的方程组.分析脉冲波在各个特征线方向的传播情况,得到近似解的一致有界性.对误差方程的解进行有效估计,得到近似解在焦点附近的较好的渐近性态.
一致 Lipschitz;球对称;几何光学;焦点
0 引 言
脉冲波是物理和光学中一种重要的波,也是自然现象中常见的波.利用偏微分方程对脉冲波的研究也是非常重要的.Carles等在文献[1-3]中研究了半线性波动方程脉冲波的传播.Alterman等在文献[4-5]中应用非线性几何光学研究了非线性脉冲波的传播性态.但在这些研究中,文献[1-3]研究的非线性项比较特殊, 且研究的都是单个波动方程的情形,而文献[4-5]研究的也是单个脉冲波的传播问题.Yuan在文献[6-7]中已将相应结果推广到波动方程组的情形,且是多个脉冲波,而且在文献[8]中研究了脉冲波的干扰产生新脉冲波的问题.
本文研究多个脉冲波的传播与干扰,将问题扩展到波动方程组,并在非线性项更加一般性的情形下讨论非线性焦散问题, 讨论脉冲波穿过聚焦点后的特性.
1 主要结论
考虑波动方程组

(1)
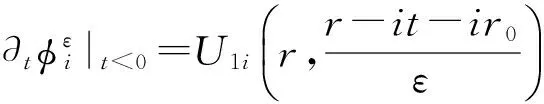
式中:r=|x|,x=(x1x2x3)∈R3,r0>0,1
suppUji(r,·)⊂[-z0,z0];i=1,2,j=0,1
(2)
而函数Fi(x,y)满足
Fi(x,y)∈C1(R2),Fi(0,0)=0
(3)
且存在常数N>0,使得对任何x,y∈R, |Fi(x,y)|≤N(|x|+|y|).
除此之外,假设Fi(x,y)(i=1,2)在R2上是一致Lipschitz的,从而易得
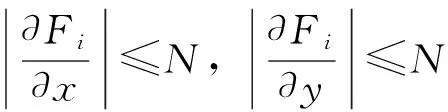
(4)
在t≥0时,系统(1)将有沿特征线4个方向的脉冲波出现,本文感兴趣的只是经过焦点(t,0)=(r0,0)的两个方向的脉冲波.
注 (1)从脉冲波干扰的角度来说,系统(1)初始条件中的特征线只要是r±t-r0之一和r±2t-2r0之一,本文结论仍成立.
(2)在t>0时,新的脉冲波就会产生,干扰项和新的脉冲波出现在二阶及二阶以上轮廓(profiles) 中[8].
由系统(1),只需考虑初值问题:
(5)
由于初值是球形对称的,假设解具有如下形式[1]:
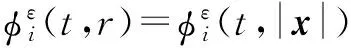
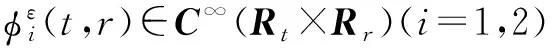
引入微分算子
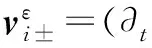
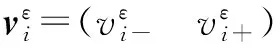
(6)
则方程组(5)转化为

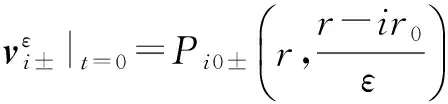
i=1,2
(7)
其中
gi(x)=2-pi|x|x,hi(y)=2-qi|y|y
(8)
Pi0±(r,z)∶=rU1(r,z)∓ir∂zU0(r,z),
Pi1(r,z)∶=U0(r,z)+ir∂rU0(r,z);i=1,2
(9)
显然Pi0±、Pi1与Uji(j=0,1,i=1,2)具有相同的性质.
由非线性几何光学得如下几个主要的轮廓:

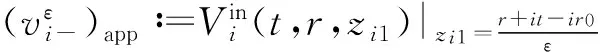
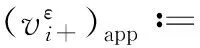
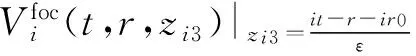
i=1,2
(10)
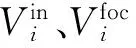
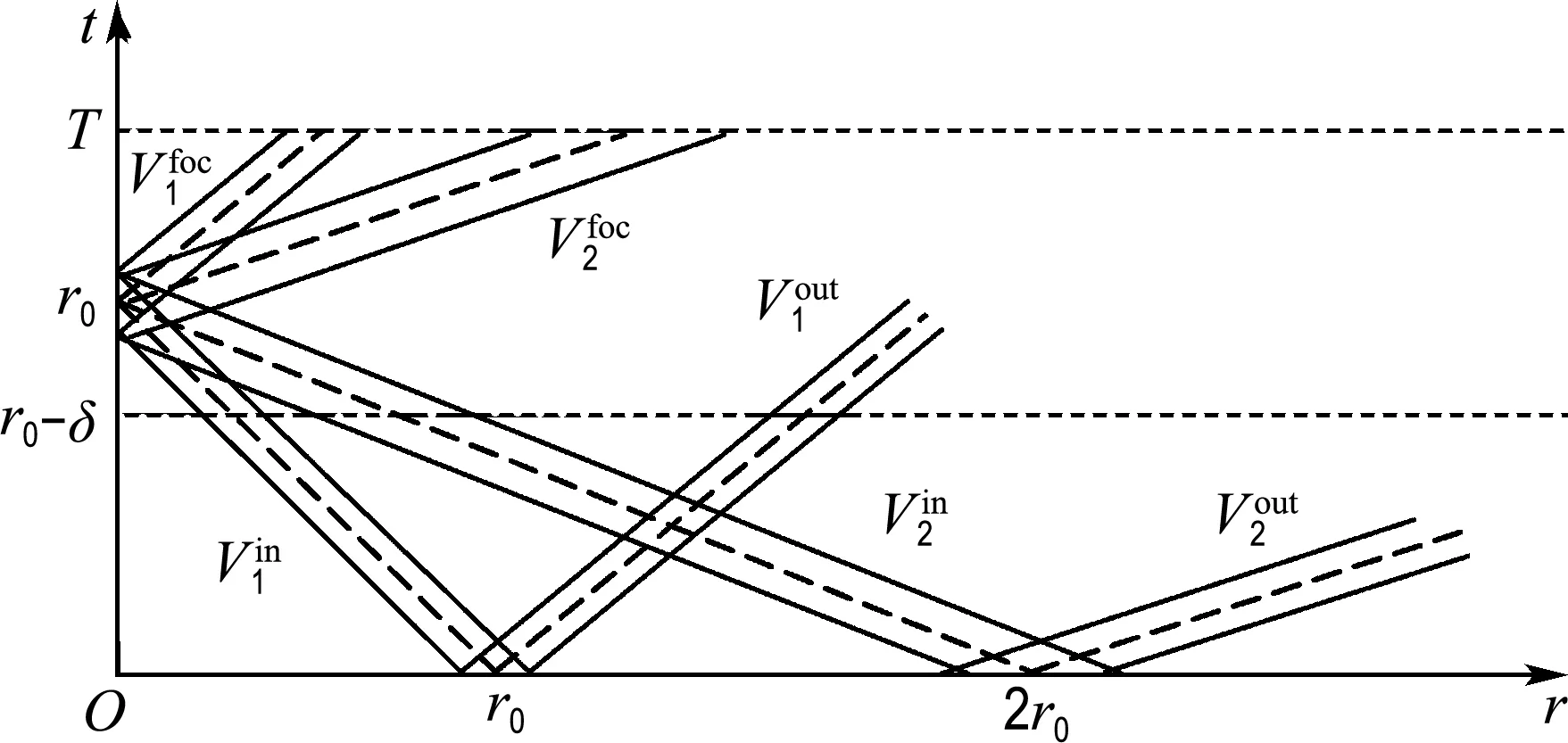
图1 射线的几何反映
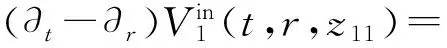
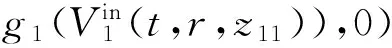
(11a)
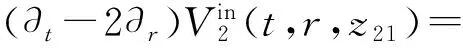
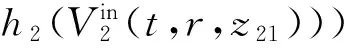
(11b)
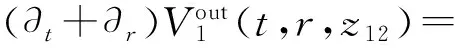
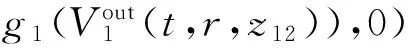
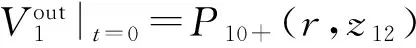
(12a)
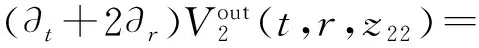
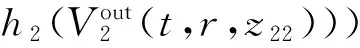
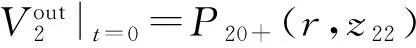
(12b)
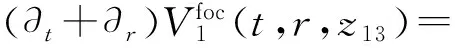
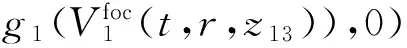
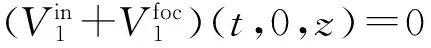
(13a)
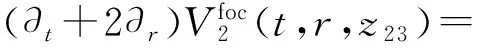
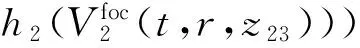
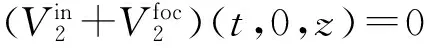
(13b)
有以下结论:
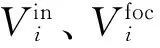
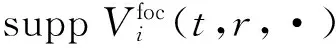
(14)
且它们关于t和z的导数是有界的,即
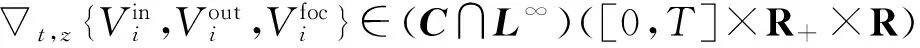
(15)
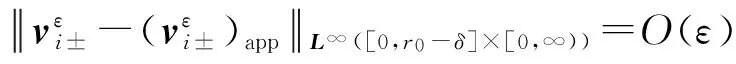
(16)
而对于穿过焦点而言,有以下估计:
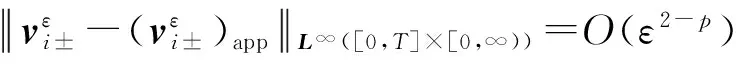
(17)
其中T>r0取定值,而p=max {p1,p2,q1,q2}.
2 主要结论的证明
2.1 准备工作
定义
(18)
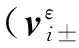
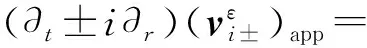
(19)
其中
(20)
fi1、fi2的具体表达式可以参照式(11)~(13).
式(19)与式(7)的第1个等式相减得
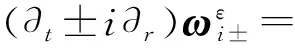
(21)
由Taylor中值定理有
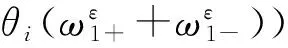
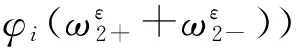
(22)
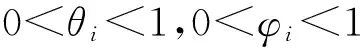
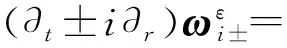
(23)
其中
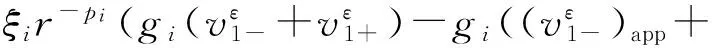
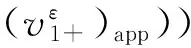
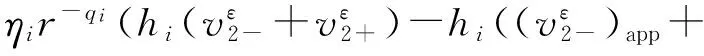
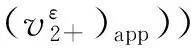
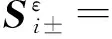
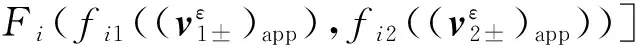
i=1,2
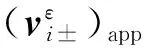
记
其中I=diag{1,1,1,1}, Λ=diag{-1,1,-2,2}.
定义1 记Γi±(T)为L在[0,T]×R+上的特征线集合,即
Γi-(T)∶={(t,r):it+r=iC,0≤t≤T,r≥0,
C∈[r0-εz0,r0+εz0]},
Γi+(T)∶={(t,r):it-r=±iC,0≤t≤T,r≥0,
C∈[r0-εz0,r0+εz0]};
i=1,2

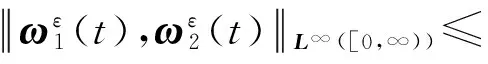
2.2 定理1的证明
在命题1中,T为解的存在区间上限,且T≥r0, 而在命题2中有
(24)
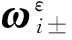
(25)
其中0 接下来需证明存在一个常数C, 使得对0<ε<1及t≤tε, 有 (26) 这就证明了tε=T.下面证明式(26)成立. 将图1中脉冲波轨迹在焦点处相交成的两个平面全等三角形区域的并记为Ei(ε),i=1,2,其表达式为 E1(ε)={(t,r):|t+r-r0|≤εz0,|t-r-r0|≤εz0}∪{(t,r):|t+r-r0|≤εz0,|t-r+r0|≤εz0} E2(ε)={(t,r):|2t+r-2r0|≤εz0,|2t-r-2r0|≤εz0}∪{(t,r):|2t+r-2r0|≤εz0,|2t-r+2r0|≤εz0} 显然有 r1-p1ζε1(t,r)χE1(ε) r1-q2r1-p1ζε2(t,r)χE2(ε) ζεi(t,r)(i=1,2) 其中在[0,T]×R+×R内是一致有界的, χ Ei(ε)为集合Ei(ε)(i=1,2)的特征函数. 式(26)得证(式(17)即得证). 现在往证式(16).对t≤r0-δ, 易得 本文研究了波动方程球形脉冲波穿过焦点的渐近性态,得到的是小初值条件下脉冲波穿过焦点的传播与干扰现象.使用了几何光学中的主要轮廓作为近似解得到结论,这在几何光学中是较普遍的方法.所得结论也满足高频振荡波所具有的性质. [1] Carles R, Rauch J. Focusing of spherical nonlinear pulses inR1+3[J]. Proceedings of the American Mathematical Society, 2000, 130(3):791-804. [2] Carles R, Rauch J. Focusing of spherical nonlinear pulses inR1+3, Ⅱ. Nonlinear caustic [J]. Revista Matematica Iberoamericana, 2004, 20(3):815-864. [3] Carles R, Rauch J. Focusing of spherical nonlinear pulses inR1+3, Ⅲ. Sub and supercritical cases [J]. Tohoku Mathematical Journal, 2004, 56 (3):393-410. [4] Alterman D, Rauch J. Nonlinear geometric optics for short pulses [J]. Journal of Differential Equations, 2002, 178(2):437-465. [5] Alterman D, Rauch J. Diffractive nonlinear geometric optics for short pulses [J]. SIAM Journal on Mathematical Analysis, 2003, 34(6):1477-1502. [6] YUAN Ming-sheng. Focusing of spherical nonlinear pulses for nonlinear wave equations [J]. Acta Mathematicae Applicatae Sinica, 2005, 21(3):415-428. [7] YUAN Ming-sheng. Spherical nonlinear pulses for the solutions of nonlinear wave equations II, nonlinear caustic [J]. Acta Mathematica Scientia, 2007, 27B(2):381-394. [8] YUAN Ming-sheng. Interaction of short pulses in a 3×3 hyperbolic system [J]. Proceedings of the Royal Society of Edinburgh, 2008, 138A(5):1163-1178. Propagation and interference of nonlinear spherical pulses at focus YUAN Ming-sheng* ( School of Business Information, Shanghai University of International Business and Economics, Shanghai 201620, China ) The behavior of the pulses like solutions to a semilinear wave equations is discussed under small initial value conditions. Using the method of nonlinear geometric optics, it is proved that the solution obtained by using the nonlinear geometric optics is effective around the focus. The propagation and interference of pulses and the production of new pulses after the interference are stated. By making use of a differential transformation, the wave equations are translated into one-order hyperbolic ones because of the spherical symmetry, and the equations for the one-order approximate solutions are obtained accordingly. The propagation of the pulses along every different characteristic line is analyzed, and the uniform boundness for the approximate solutions is obtained. Finally, by effectively estimating the solutions for the error equations, the good asymptotic behavior of the approximate solutions is testified around the focus. uniform Lipschitz; spherical symmetry; geometric optics; focus 1000-8608(2016)02-0176-05 2015-05-31; 2015-09-22. 中央财政支持地方高校发展专项资金资助项目(YC-XK-13107). 袁明生*(1964-),男,教授,E-mail:msyuan2006@suibe.edu.cn. O175.27 A 10.7511/dllgxb201602010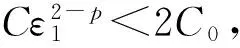
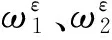
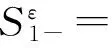

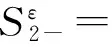
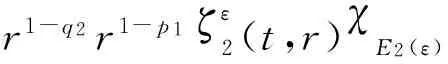
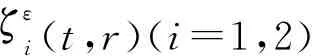
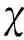
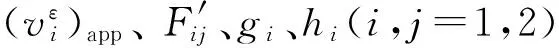
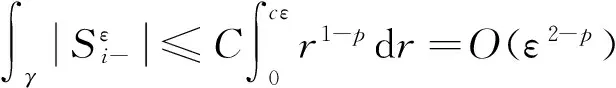
3 结 语
