动水压力对高桩承台连续刚构桥地震反应的影响

曹梦强

（四川建筑职业技术学院 交通与市政工程系，四川 德阳 618000）

动水压力对高桩承台连续刚构桥地震反应的影响

曹梦强

（四川建筑职业技术学院 交通与市政工程系，四川 德阳 618000）

以某高桩承台连续刚构桥为工程背景，采用Morison方程计算不同水深时的动水压力，并利用纤维模型对地震作用进行非线性时程反应分析。结果表明：动水压力会改变桥梁的自振特性，随着水深的增加，桥梁地震反应也越来越大，在进行桥梁设计时应考虑动水压力的影响。

桥梁工程；连续刚构桥；动水压力；Morison方程；地震反应

随着经济的发展，桥梁设计和施工技术水平也有了很大的进步，跨江、跨河、跨海桥梁的建设项目也越来越多，而我国又是一个地震频发的国家，地震对桥梁的破坏不但会造成重大的经济损失，还会对社会环境造成很大影响，因此有必要对深水中的桥梁进行较为精确的地震反应分析，其中关于墩-水相互作用的研究尤为关键。袁迎春等研究了拖拽力对柱底固结的小直径直立柱体的地震反应的影响，得出拖拽力对结构地震反应影响很小的结论，并认为对结构进行地震反应分析时可以忽略拖拽力的影响［1］。本文采用Morison方程，结合纤维模型对动水压力下某刚构桥的地震反应进行分析。

1 基于Morison方程的桥梁供水压力计算

Morison方程将动水压力按两部分来计算，一部分是由流体的黏滞效应而引起的拖拽力，另一部分则是由附加质量效应而引起的惯性力。

设处于水中的铅直柱体的运动位移为x，波浪水质点在柱体轴中心位置处的水平位移为u，地面运动位移为xg，由 Morison 方程，单位长度铅直柱体上沿x轴方向的波浪力为［2-4］：

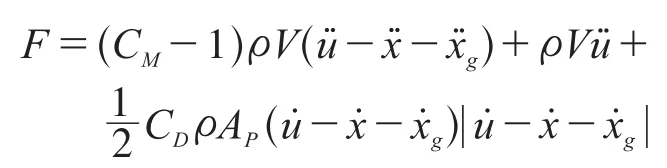
式中：ρ为水的密度；V为单位长度柱体的体积；AP为单位长度柱体在垂直于波浪运动方向上的投影面积；和为水的绝对速度和绝对加速度；和为柱体结构的相对速度和相对加速度；g和g为地面运动速度和加速度；CM为动水惯性力系数；CD为动水阻力系数。

假定水流速度为零，同时 Morison 方程忽略了结构存在对水的影响，结构运动不会产生水的运动，这样水的速度和加速度都为零［2-4］。则上式就可以写成

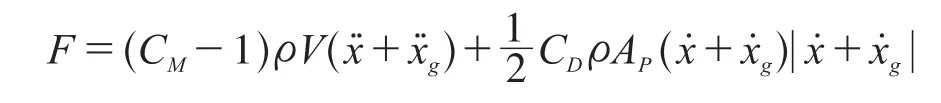
式中：（CM-1）ρV为柱体单位长度上的动水附加质量；为柱体单位长度上的动水附加阻尼。

由 Morison 方程建立考虑动水压力的结构在地震作用下的运动方程为：

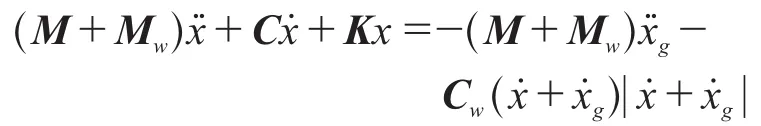
式中：M、K和C分别为结构的质量、刚度和阻尼矩阵；Mw和Cw分别为由Morison 方程得到的结构附加质量和附加阻尼矩阵。

在有限元模型中，Mw和Cw的元素可按下式计算：

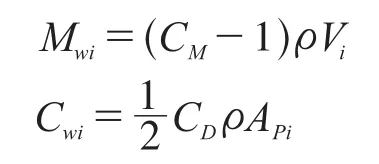
式中：Mwi为第i个单元的附加质量；Cwi为第i个单元的附加阻尼。

以上公式都是由圆柱体推导出来的，对于桥梁中常见的矩形桥墩（见图1），其单位高度上的动水附加质量可通过等效圆柱体单位高度上的动水附加质量乘以一个修正系数Kc得到［5］，即：

式中：D为垂直于柱体运动方向的截面尺寸；B为平行于柱体运动方向的截面尺寸；为矩形截面柱体单位高度上的动水附加质量；为直径为D的等效圆柱体单位高度上的动水附加质量。

图1 不同截面换算关系

利用文献［6］给出的试验数据，得到以矩形截面形状参数D/B为参数的修正系数的近似计算公式：

对于群桩基础，桩与桩之间会产生干扰效应和遮蔽效应，并且这2种效应会随着桩间距的增大而减小。设l为桩柱中心距，D为桩柱直径，当l/D≥4时，可以忽略干扰效应和遮蔽效应；当l/D＜4时，则必须考虑干扰效应和遮蔽效应［4］，计算动水质量时应将作用于单桩上的动水压力乘以相应的群桩系数（见表1）。根据以上计算得到桥梁各部位的动水附加质量见表2。

表1 群桩系数

表2 动水附加质量 t

2 动水压力下桥梁地震反应分析

预应力混凝土连续刚构桥的跨径为（68+125+ 68）m，横断面为单箱单室直腹板，采用高桩承台桩基础。河床表面为较薄的卵石层，其下均为砂质泥岩。总体布置图如图2所示。混凝土等级主梁为C55，墩身为C35，承台和基础为C30，设计基本地震加速度峰值为0.20 g。桩-土相互作用采用土弹簧模拟，土弹簧刚度采用m法计算［8］。混凝土的本构采用Mander模型，钢材的本构采用Menegotto-Pinto模型；非弹性铰特性值采用kinematic hardening滞回模型，由此建立的纤维模型如图3所示。

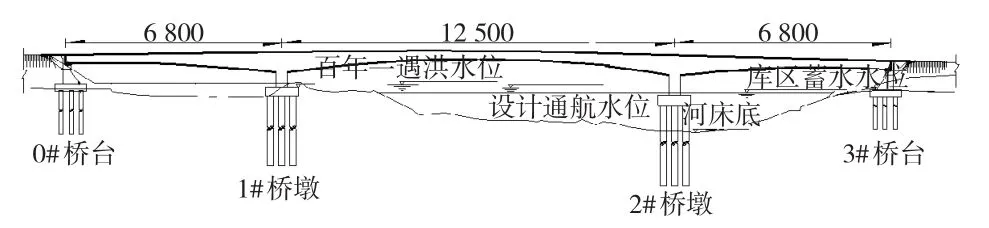
图2 总体布置图（单位：cm）

图3 全桥模型

采用El Centro波进行非线性时程反应分析，其加速度时程曲线和傅里叶谱曲线如图4和图5所示，从傅里叶谱曲线中可以看出El Centro波的卓越频率为1.47 Hz。

对相对水深为0%、45%、65%和100%时全桥的地震响应进行分析，其中相对水深=（水深/河床以上下部结构高度）×100%，而河床以上下部结构高度包括河床以上的桩身高度（9 m）、承台高度（3.5 m）和墩身高度（6.5 m）。桥梁处于不同水深时前5阶自振频率和振型特征见表3。由表可知，随着水深的增加，施加在结构上的动水附加质量也增加，所以自振频率会减小。

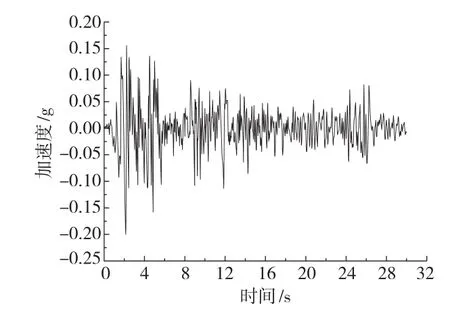
图4 加速度时程曲线

图5 傅里叶谱曲线

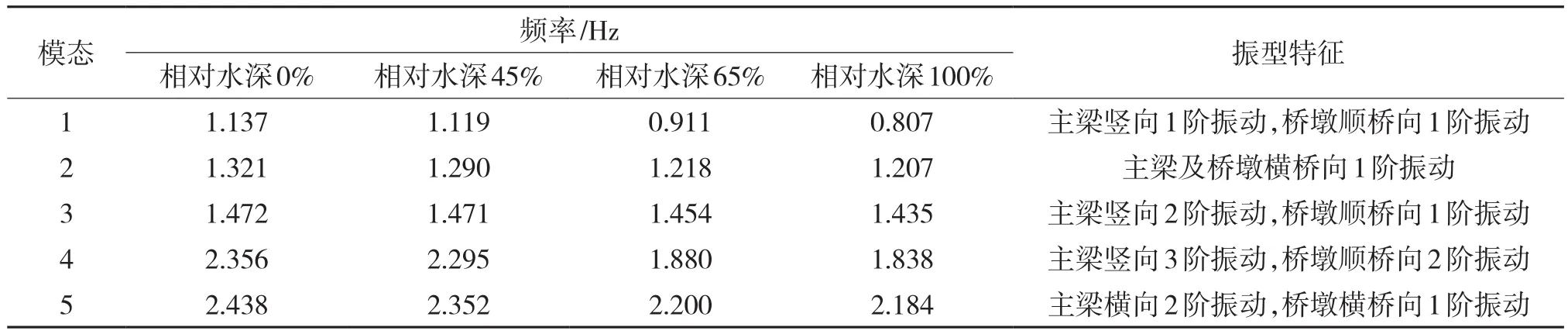
表3 自振特性

表4为全桥在El Centro波作用下2#桥墩的墩顶位移和墩底内力，从表中可以看出，无论顺桥向还是横桥向墩顶位移均随水深的增加而增大，在相对水深为65%时顺桥向的墩底轴力、墩底剪力和墩底弯矩达到最大值，以后随着水深的增加而减小；在相对水深为45%时横桥向的墩底轴力、墩底剪力和墩底弯矩达到最大值，以后随着水深增加而减小，说明桥梁已进入塑性且横桥向要比顺桥向更易进入塑性。

图6和图7为2#桥墩墩顶位移在不同水深时与无水时的时程曲线，从曲线中可以看出，在同一时刻有水时的墩顶位移均要大于无水时的墩顶位移，说明动水附加质量会增大桥梁的地震反应，且水深越大地震反应也越大。

Influence of Hydrodynamic Pressure on Seismic Response of Continuous Rigid Frame Bridge with Elevated Pile Pier

Cao Mengqiang
（Department of Transportation and Municipal Engineering, Sichuan College of Architectural Technology, Deyang 618000, China）

Take a continuous rigid frame bridge with elevated pile pier as an engineering background, hydrodynamic pressure are calculated with Morison equation under the condition of different water depth, on this base, the nonlinear time history response is analyzed by establishing fiber model. Results show that hydrodynamic pressure can change the natural vibration characteristics of bridge, and seismic response increases with the increase of water depth, therefor the effect of hydrodynamic pressure must be considered.

bridge engineering; continuous rigid frame bridge; hydrodynamic pressure; Morison equation; seismic response

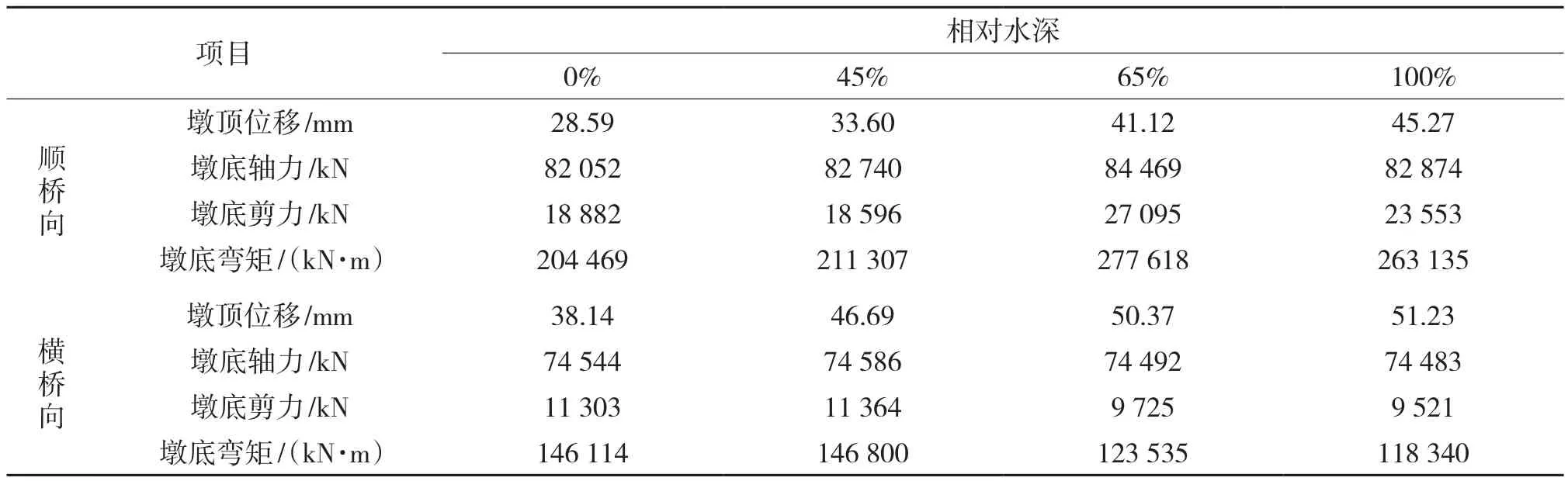
表4 墩顶位移和墩底内力

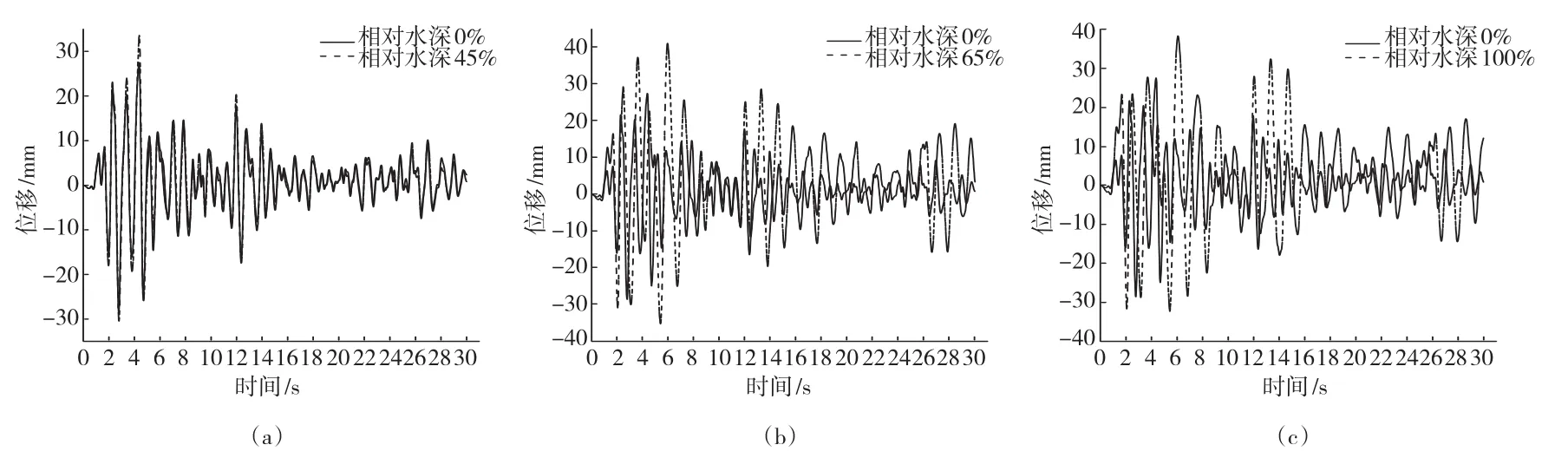
图6 顺桥向墩顶位移时程曲线

U442.59

A

1672-9889（2016）05-0030-03

曹梦强（1986-），男，重庆人，硕士研究生，研究方向为桥梁抗震。