高墩桥梁墩柱计算长度分析

张宏华

（盐城市第二交通工程处，江苏 盐城 224005）

高墩桥梁墩柱计算长度分析

张宏华

（盐城市第二交通工程处，江苏 盐城 224005）

桥墩计算长度是高墩连续梁桥墩柱设计的一个重要参数。文章首先比较分析了各国规范对于标准约束条件下桥墩计算长度系数的规定；然后根据最小势能原理，考虑墩底约束刚度、墩顶约束刚度的影响，推导了桥墩计算长度系数的计算公式；最后详细讨论了约束刚度取值对桥墩计算长度系数的影响。研究结论表明墩底约束刚度、墩顶转动刚度对桥墩计算长度系数影响较小；桥墩计算长度系数随着墩顶水平刚度增加而迅速减小，而后趋于稳定。

桥梁工程；高墩；计算长度系数；能量法；参数分析；约束刚度

在高墩连续梁桥的设计计算中，桥墩计算长度是十分重要的参数，但是一直以来没有关于计算长度的明确算法［1-5］。桥墩的顶部并非完全自由或完全固结，而是具有一定刚度的约束，桥墩的底部也非完全固结，也具有一定的柔度。复杂的边界条件，以及墩身截面特性的变化使得桥墩计算长度的求解具有一定的困难［6-8］。目前工程设计实践中，一般根据上部结构和地基基础情况，采用1～2.5的经验值［9］，为避免造成的桥墩设计过于保守或者处于不安全状态，有必要对其取值进行深入研究。

1 相关规范规定

国内外规范对桥墩计算长度的理解基本相近，但对不同支承条件的桥墩计算长度系数的规定又不尽相同［10］，如表1所示，其中美国AASHTO规范推荐采用接近于理论值的近似值，表中括号内为理论值。

从表中可以看出，我国公路桥梁规范给出的桥墩计算长度采用的是理想支承条件下的理论计算值，而美国规范和英国规范则考虑了实际工程状态，对不同的支承条件下的理论值进行修正，桥墩计算长度系数有所提高。与欧美规范相比，我国公路桥梁规范给出的桥墩计算长度系数偏小，偏于不安全。

2 计算方法分析

桥墩计算长度系数的取值是由桥墩的失稳荷载反算得到的。结构失稳有2种类型：分支点失稳和极值点失稳。分支点失稳是指结构从初始平衡位置转变到另一平衡位置，也称为屈曲。研究压杆稳定问题常用的方法有静力平衡法、能量法、缺陷法、振动法等。本文基于能量法中的最小势能原理给出桥墩计算长度的计算方法。

表1 各国规范中关于桥墩计算长度系数的规定

设结构在外力系作用下处于初始平衡状态，受到外力扰动后，在平衡位置的足够小邻域内发生某一可能位移，称为虚位移，则体系的总势能将产生一个增量。

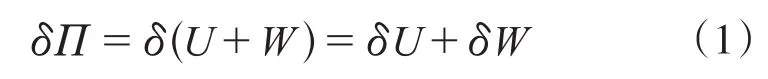
式中：Π为总势能；U、W分别为结构的应变能和荷载势能；δ为增量。

在一切满足边界条件的虚位移中，同时满足平衡条件的虚位移对应于结构势能的一个驻值，这就是结构势能驻值原理。对于线弹性结构，势能二阶变分恒为正，因为使总势能取最小值，所以这个原理又称最小势能原理。

瑞利-利兹法是基于变分原理求解势能驻值的一种近似解法。假定发生分支点失稳时的位移函数为y（x），对于任一杆件，可用广义坐标表达为：

式中：αi为广义坐标的独立参数；fi（x）为位移形函数，要求满足杆端变形条件。

由于变分δαi不等于0，所以有：

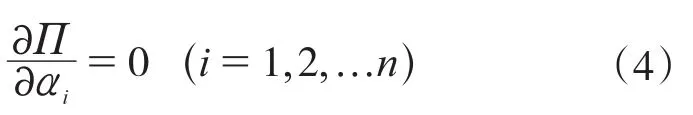
求解上述方程，即可求得临界荷载。

这种近似方法的精度取决与位移函数y（x）的选择。设桥墩高为l，墩顶作用一竖向力P，考虑桥墩墩顶支座约束和墩底基础约束作用，墩顶支座采用平动弹簧、转动弹簧模拟，基础变位影响用平动弹簧、转动弹簧模拟，平动和转动的耦合项做平转耦合弹簧模拟，不考虑竖向变位对墩的影响，桥墩的计算模型如图1所示。

图1 力学模型示意图

墩身形函数取墩底固结时的弹性变形与由转动弹簧所产生的刚体转动位移及刚体平动位移之和。对墩身形函数采用三次多项式表示，而刚体位移则用线函数表示。则墩身的位移形函数为：

将几何边界条件引入：

将式（5）、式（6）带入式（4）进行求解，即可求得临界荷载Pcr，继而可由欧拉公式解出计算长度系数 μ：

桥墩的计算长度系数的求解计算流程如图2所示。

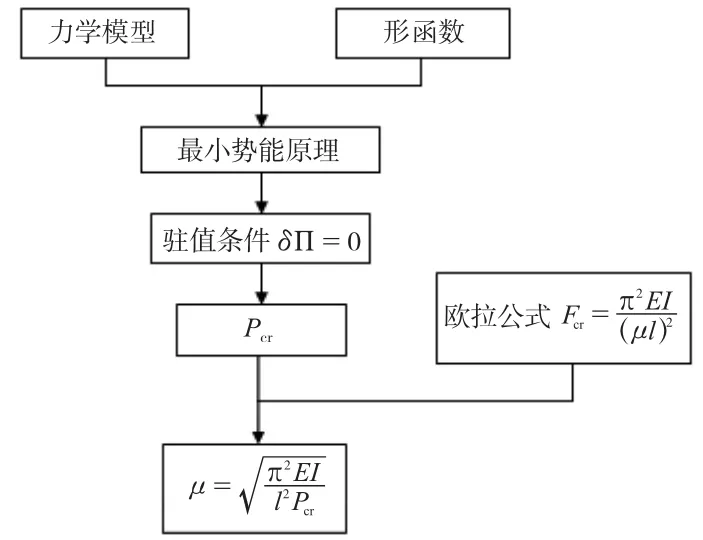
图2 计算流程图

3 参数分析

从上面的推导可以看出，桥墩的计算长度系数除了与墩顶约束刚度、墩底约束刚度有关，和墩柱的材料弹性模量、抗弯惯性矩、高度等都有关系。实际工程中，高墩一般指40 m以上的桥墩，100 m以上的桥墩应用较少。为便于研究，本文取40～100 m的桥墩作为研究对象。

3.1 墩底约束刚度

高墩的墩底约束刚度与采用的基础形式有关，一般情况下，根据静力计算确定的基础刚度都很大。采用桩基础的墩底约束刚度可用m法进行求解。

墩高60 m、直径2.2 m时，不同基础刚度下的计算长度系数如图3所示。可以看出，基础刚度越大，计算长度系数越小，但总的来说，基础刚度的变化对计算长度系数取值的影响不大。正常设计条件下，可按墩底固结进行简化计算。

图3 计算长度系数与基础刚度关系图

3.2 墩顶约束刚度

高墩的墩顶约束刚度与采用的支座形式以及结构体系有关，应考虑连续梁各墩的抗推刚度后按集成刚度法分配给计算墩。

墩高60 m、直径2.2 m时，不考虑墩顶转动刚度，不同墩顶水平刚度下的计算长度系数如图4所示。可以看出，桥墩计算长度系数随着墩顶水平刚度增加而迅速减小，水平刚度超过4 000 kN/m时，计算长度系数趋于稳定。

图4 计算长度系数与墩顶水平刚度关系图

墩高60 m、直径2.2 m，墩顶水平刚度1 000 kN/m时，不同墩顶转动刚度下的计算长度系数如图5所示。可以看出，桥墩计算长度系数随着墩顶转动刚度增加而减小，但变化很小。正常设计条件下，可忽略墩顶转动刚度的影响。

图5 计算长度系数与墩顶转动刚度关系图

4 结论

（1）计算长度系数随着基础刚度的增加而减小，但总的来说，基础刚度的变化对计算长度系数取值的影响不大。正常设计条件下，可按墩底固结进行简化计算。

（2）桥墩计算长度系数随着墩顶水平刚度增加而迅速减小，水平刚度超过一定数值时，计算长度系数趋于稳定。

（3）桥墩计算长度系数随着墩顶转动刚度增加而减小，但变化很小，正常设计条件下，可忽略墩顶转动刚度的影响。

［1］高小妮，贺拴海，齐宏学.考虑桩基柔度的多跨梁桥高墩计算长度系数分析［J］.武汉理工大学学报，2011（7）：88-93.

［2］徐润，叶建国，孙志刚.柔性桥墩计算长度的简化计算研究［J］.中外公路，2012（3）：134-137.

［3］梁雄，周建庭，刘承，等.连续梁桥桥墩顺桥向计算长度系数研究［J］.公路交通科技，2013（7）：82-88.

［4］单昊，黄杨彬.简支梁桥的高墩计算长度分析［J］.公路交通科技(应用技术版)，2014（4）：207-209.

［5］曾照亮.高墩计算长度探讨［J］.中外公路，2008，28（5）：160-162.

［6］刘睿.变截面墩柱计算长度理论研究［D］.重庆：重庆交通大学，2011.

［7］海青.单排桩柱墩压杆的计算长度［J］.福州大学学报，2007，31（1）：89-94.

［8］潘志炎，史方华.高桥墩稳定性分析［J］.公路，2004（9）： 60-62.

［9］ 雷博.梁式桥高墩计算长度研究［D］.长安大学，2013.

［10］冯云成，宋松林.采用单阶柱法分析连续体系梁式桥桥墩的计算长度［J］.桥梁建设，2013（1）：78-82.

Study on Effective Length of Pier Column of High-pier Bridge

Zhang Honghua
（The Second Traffic Engineering Department of Yancheng City, Yancheng 224005, China）

Effective length of high-pier is an important parameter for the design of continuous girder bridge with high piers. Firstly, comparative analysis of regulation of pier effective length factor under the standard constraints is promoted according to different countries standards. Then based on the principle of minimum potential energy, calculation formulas of pier effective length factor are derived, considering restraining stiffness of bottom and top of high-pier. At last, the impact of restraining stiffness values on pier effective length factor is discussed in detail. The results show that restraint stiffness of pier bottom and rotational stiffness of pier top have little influence on pier effective length factor, but the factor decreases rapidly with the horizontal stiffness of pier top increasing. When the horizontal stiffness exceeds certain value, the factor becomes stable.

bridge endineering; high-pier; effective length factor; energy method; parameter analysis; restraining stiffness

U442.5

A

1672-9889（2016）05-0027-03

2015-11-09）

张宏华（1972-），男，江苏盐城人，工程师，主要从事道路、桥梁技术管理工作。