涡桨发动机高速转子临界转速调整措施分析

邓旺群，范潘潘，袁胜，何萍，夏锟

(1.中国航空动力机械研究所，湖南株洲412002；2.航空发动机振动技术航空科技重点实验室，湖南株洲412002)

涡桨发动机高速转子临界转速调整措施分析

邓旺群1，2，范潘潘1，2，袁胜1，2，何萍1，夏锟1，2

(1.中国航空动力机械研究所，湖南株洲412002；2.航空发动机振动技术航空科技重点实验室，湖南株洲412002)

针对支承刚度、轮盘质量、低压轴壁厚对涡桨发动机低压模拟转子临界转速的影响开展研究，为临界转速的调整试验提供理论依据。采用有限元方法建立了低压模拟转子的计算模型，在不同支承刚度、轮盘质量和低压轴壁厚下，利用SAMCEF/ROTOR分析软件对转子前三阶临界转速进行了系统计算，揭示了转子前三阶临界转速随支承刚度、轮盘质量和低压轴壁厚的变化规律，并提出了相应的调整措施，具有工程应用价值。

航空发动机；转子动力学；低压模拟转子；有限元法；临界转速；变化规律；调整措施

1　引言

临界转速是转子动力学的核心内容，也是转子设计过程中的一个重点考虑因素。对于航空发动机，合理配置转子的临界转速是保证发动机安全可靠运行的前提[1]。影响转子临界转速的因素主要有转子的刚度分布、质量分布、结构形式等[2]，一些学者对此开展了研究。国外Chiang等对透平机械的单转子和双转子系统进行了相关分析[3]；国内白中祥等[4-5]研究了支承刚度对临界转速的影响；洪杰等[6]研究了转子支承动刚度对转子动力特性的影响；李海伟[7]基于ANSYS建立了转子有限元模型，并分析了转子临界转速随支承主刚度与主阻尼的变化规律；聂卫健等[8]研究了高速柔性转子临界转速随支承刚度和轮盘质量的变化规律；邓旺群等[9]以涡扇发动机低压转子为研究对象，分析了不同支承刚度对临界转速的影响。

本文以某涡桨发动机低压模拟转子为研究对象，采用控制变量法系统分析了支承刚度、轮盘质量和低压轴壁厚变化对转子临界转速的影响，揭示了转子前三阶临界转速随支承刚度、轮盘质量和低压轴壁厚的变化规律，为该转子临界转速的调整试验提供了理论依据。

2　低压模拟转子结构及计算模型

低压模拟转子具有多盘、带空心轴和止口定心传扭轮盘的结构特点。如图1所示，该转子主要由模拟压气机轮盘、模拟涡轮盘、低压轴及中心拉杆等零部件组成，采用1-1-1三支点支承方式。其中1号和3号轴承为滚棒轴承，2号轴承为滚珠轴承。1号轴承位置有鼠笼式弹性支承和挤压油膜阻尼器，2号轴承位置为刚性支承且没有挤压油膜阻尼器，3号轴承位置有弹性环式弹性支承。模拟压气机轮盘材料为钛合金，模拟涡轮盘为不锈钢。

为准确计算转子的临界转速，首先必须建立能反映转子实际的计算模型。传统的传递矩阵法适合计算链式结构转子，不适合计算复杂结构转子。复杂结构转子的建模普遍采用有限元法，以保证计算模型的完整性和准确性。建模前对低压模拟转子局部结构进行简化，忽略倒角、小孔等结构。同时，为方便建模，将模拟压气机轮盘和模拟涡轮盘的部分结构去掉，作集中质量处理，考虑转动惯量。采用轴对称单元模拟转子各零部件的结构特征，应用PATRAN软件对转子进行梁单元网格划分。然后将划分好网格的模型导入转子动力学专用分析软件SAMCEF/ROTOTR，并在该软件中添加质量单元、轴承单元和刚性连接单元。图2为建立的有限元计算模型，该模型共有5个集中质量单元，3个轴承单元，40个刚性连接单元和1 217个梁单元。

图1　低压模拟转子的结构示意图Fig.1 Structure of the low-pressure simulation rotor

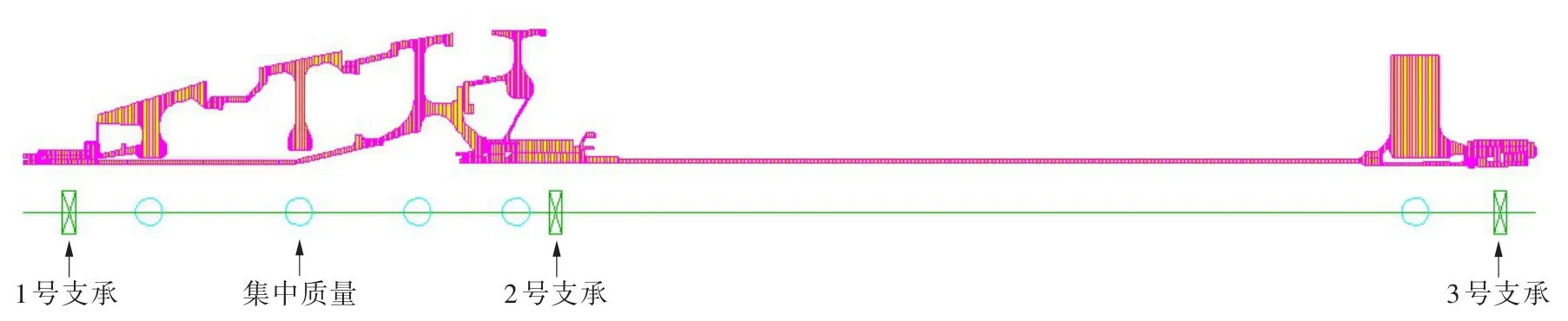
图2　低压模拟转子的有限元计算模型Fig.2 Finite element calculation model of the low-pressure simulation rotor

3　临界转速随支承刚度的变化规律

低压模拟转子三个支点的设计支承刚度(基准值)分别为2.5×107N/m、6.0×107N/m、0.5×107N/m。在该刚度组合下，前三阶临界转速对工作转速的计算裕度均大于20%，转子临界转速设计合理[2]。

3.1临界转速随1号支承刚度的变化规律

当2号和3号支承刚度取基准值，1号支承刚度在基准值附近变化(变化范围1.0×107N/m～4.0×107N/m)时，通过计算得到低压模拟转子的前三阶临界转速随1号支承刚度的变化曲线(图3)，再由变化曲线图可得到前三阶临界转速随1号支承刚度的变化率(表1)。

从图3和表1可知：在1号支承刚度变化范围内，前三阶临界转速随着1号支承刚度的增大而增大；改变1号支承刚度，可有效调节第二阶临界转速，对第三阶临界转速也有一定的调节效果，但对第一阶临界转速的调节效果不明显。

3.2临界转速随2号支承刚度的变化规律

当1号和3号支承刚度取基准值，2号支承刚度在基准值附近变化(变化范围4.5×107N/m～7.5×107N/m)时，通过计算得到低压模拟转子的前三阶临界转速随2号支承刚度的变化曲线(图4)，再由变化曲线图可得到前三阶临界转速随2号支承刚度的变化率(表2)。

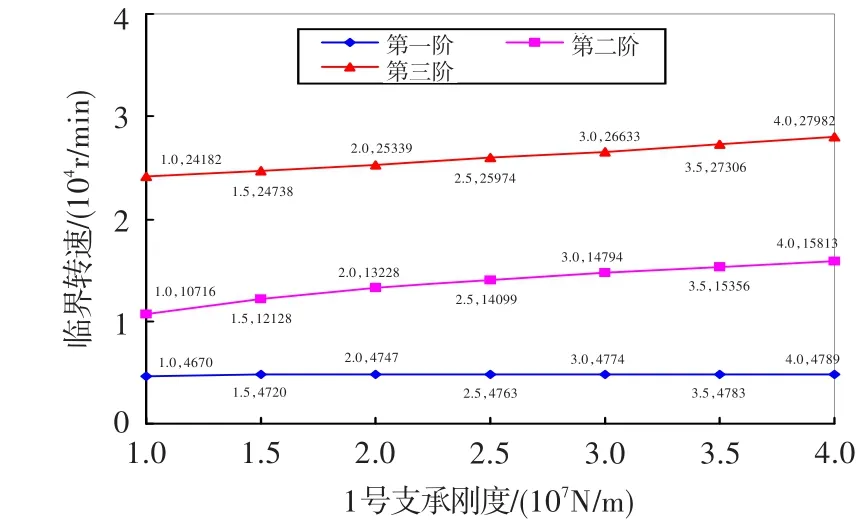
图3　前三阶临界转速随1号支承刚度的变化曲线Fig.3 Curves of first three stage critical speed with No.1 supporting stiffness

表1　前三阶临界转速随1号支承刚度的变化率Table 1 Change rate of the first three stage critical speed with No.1 supporting stiffness

图4　前三阶临界转速随2号支承刚度的变化曲线Fig.4 Curves of first three stage critical speed with No.2 supporting stiffness

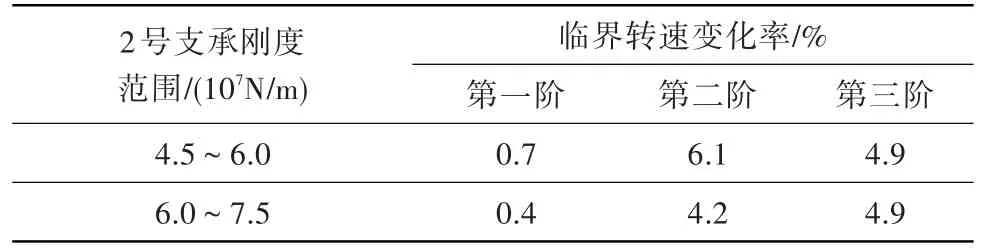
表2　前三阶临界转速随2号支承刚度的变化率Table 2 Change rate of the first three stage critical speed with No.2 supporting stiffness

从图4和表2可知：在2号支承刚度变化范围内，前三阶临界转速随着2号支承刚度的增大而增大；改变2号支承刚度，对第二阶和第三阶临界转速有一定的调节效果，但对第一阶临界转速的调节效果甚微。

3.3临界转速随3号支承刚度的变化规律

当1号和2号支承刚度取基准值，3号支承刚度在基准值附近变化(变化范围0.3×107N/m～0.8×107N/m)时，通过计算得到低压模拟转子的前三阶临界转速随3号支承刚度的变化曲线(图5)，再由变化曲线图可得到前三阶临界转速的变化率(表3)。

图5　前三阶临界转速随3号支承刚度的变化曲线Fig.5 Curves of first three stage critical speed with No.3 supporting stiffness

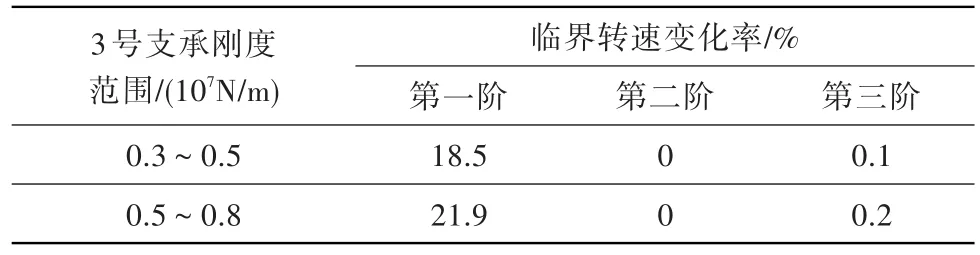
表3　前三阶临界转速随3号轴承刚度的变化率Table 3 Change rate of the first three stage critical speed with No.3 supporting stiffness

从图5和表3可知：在3号支承刚度变化范围内，第一阶临界转速随着3号支承刚度的增大而增大，第二阶和第三阶临界转速几乎没有变化或变化很小；改变3号支承刚度，可有效调节第一阶临界转速，但对第二阶和第三阶临界转速几乎没有调节效果。

4　临界转速随轮盘质量的变化规律

保持支承刚度和转子结构不变，研究前三阶临界转速随轮盘质量(改变材料)的变化关系。由于模拟涡轮盘的材料一般为高温合金或不锈钢，改变材料对临界转速的影响有限，因此只研究模拟压气机轮盘材料对临界转速的影响。

支承刚度值为设计支承刚度(基准值)，模拟压气机轮盘可选材料属性见表4。模拟压气机轮盘质量变化时，通过计算得到低压模拟转子的前三阶临界转速随模拟压气机轮盘质量的变化曲线，见图6，由图6可得到前三阶临界转速随模拟压气机轮盘质量的变化率，见表5。

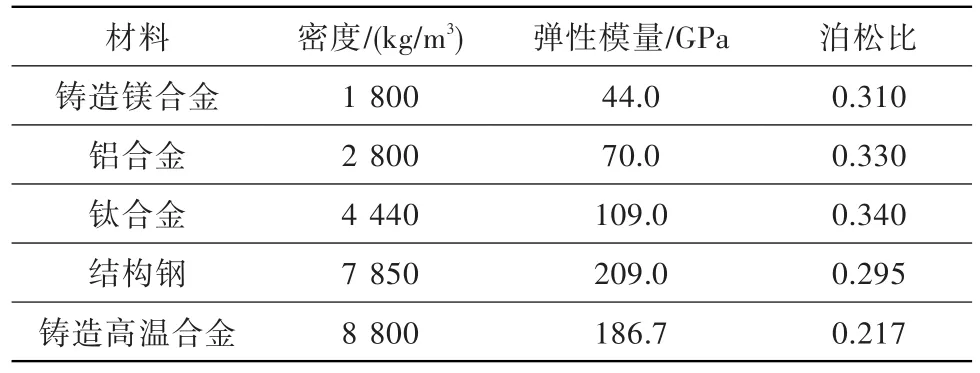
表4　模拟压气机轮盘可选材料属性Table 4 Properties of materials

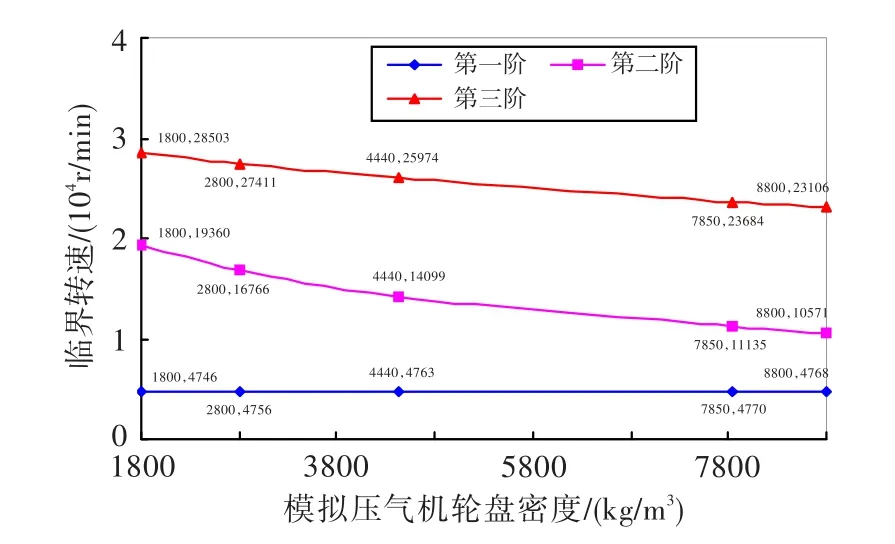
图6　前三阶临界转速随模拟压气机轮盘质量的变化曲线Fig.6 Curves of first three stage critical speed with qualities of simulated compressor disk

表5　前三阶临界转速随模拟压气机轮盘质量的变化率Table 5 Change rate of the first three stage critical speed with qualities of simulated compressor disks

从图6和表5可知：模拟压气机轮盘质量变化时，第一阶临界转速随轮盘质量的增大基本没有变化，第二阶和第三阶临界转速逐步减小；改变模拟压气机轮盘质量，可有效调节第二阶和第三阶临界转速，其中对第二阶临界转速的调节效果尤其显著。

5　临界转速随低压轴壁厚的变化规律

保持支承刚度和轮盘质量不变，仅改变低压轴壁厚来研究前三阶临界转速随低压轴壁厚的变化关系。支承刚度为设计支承刚度(基准值)，轮盘材料为设计选用材料。当低压轴壁厚在3.5 mm(设计值)至45 mm(此时为实心轴)范围内变化时，通过计算得到低压模拟转子的前三阶临界转速随低压轴壁厚的变化曲线(图7)，再由变化曲线图可得到前三阶临界转速随低压轴壁厚的变化率(表6)。

图7　前三阶临界转速随低压轴壁厚的变化曲线Fig.7 Curves of first three stage critical speed with wall thickness of low-pressure shaft

表6　前三阶临界转速随低压轴壁厚的变化率Table 6 Change rate of the first three stage critical speed with wall thickness of low-pressure shaft

从图7和表6可知：随着低压轴壁厚的增大，前三阶临界转速逐步减小；低压轴壁厚在3.5～25.0 mm范围内变化时，可有效调节第三阶临界转速，对第一阶和第二阶临界转速有一定的调节效果；低压轴壁厚在25.0～45.0 mm范围内变化时，对前三阶临界转速的调节效果均十分有限。

6　结论

(1)改变3号支承刚度，可有效调节第一阶临界转速；改变1号支承刚度，可有效调节第二阶临界转速；但支承刚度的改变，对第三阶临界转速的调节效果有限。

(2)改变模拟压气机轮盘材料，可有效调节第二阶和第三阶临界转速，其中对第二阶临界转速的调节效果尤其显著，但对第一阶临界转速几乎没有调节效果。

(3)低压轴壁厚在3.5～25.0 mm范围内变化时，可有效调节第三阶临界转速，对第一阶和第二阶临界转速有一定的调节效果。

(4)改变支承刚度的成本低、操作性强且无需改变转子结构，应优先选择通过改变支承刚度来调节转子的临界转速。

[1]顾家柳，丁奎元，刘启周，等.转子动力学[M].北京：国防工业出版社，1985：59—60.

[2]《航空发动机设计手册》总编委会.航空发动机设计手册：第19册——转子动力学及整机振动[K].北京：航空工业出版社，2000：8—23.

[3]Chiang H W D，Hsu C N，Tu S H.Rotor-bearing analysis for turbo machinery single-and dual-rotor systems[J]. Journal of Propulsion and Power，2004，20(6)：1096—1104.

[4]白中祥，吴伟亮.转子支承系统的刚度对其临界转速的影响[J].机电设备，2012，29(5)：46—49.

[5]白中祥，吴伟亮，刘闳钊.支承系统的刚度对转子动力特性的影响[J].机械设计与研究，2012，28(4)：18—21.

[6]洪杰，王华，肖大为，等.转子支承动刚度对转子动力特性的影响分析[J].航空发动机，2008，34(1)：23—27.

[7]李海伟.支承参数对转子临界转速的影响分析[J].上海电气技术，2014，7(1)：48—52.

[8]聂卫健，邓旺群，徐友良，等.高速柔性转子临界转速随支承刚度和轮盘质量的变化规律[J].燃气涡轮试验与研究，2015，28(3)：19—24.

[9]邓旺群，聂卫健，何萍，等.高速柔性转子临界转速随支承刚度的变化规律[J].噪声与振动控制，2015，35(3)：98—101.

Critical speed adjustment measure analysis for high-speed rotor of a turboprop engine

DENG Wang-qun1，2，FAN Pan-pan1，2，YUAN Sheng1，2，HE Ping1，XIA Kun1，2
(1.China Aviation Powerplant Research Institute，Zhuzhou 412002，China；2.Aviation Key Laboratory of Aero-engine Vibration Technology，Zhuzhou 412002，China)

Influence of supporting stiffness,masses of disk and wall thickness of low-pressure shaft on critical speed of low-pressure simulation rotor of a turboprop engine was researched to provide theoretical bases for adjustment experiment of critical speed.Calculation model of the low-pressure simulation rotor was established by finite element method.The first three stage critical speed of the rotor was systematically calculated by SAMCEF/ROTOR software based on different supporting stiffness,masses of disk and wall thickness of the low-pressure shaft.According to results of data analysis,the change laws of first three stage critical speed with different supporting stiffness,masses of disk and wall thickness of the low-pressure shaft were revealed.Adjustment measures of application value in engineering of critical speed of the rotor were put forward.

aero-engine；rotor dynamics；low-pressure simulation rotor；finite element method；critical speed；change law；adjustment measure

V231.96

A

1672-2620(2016)05-0021-04

2016-04-22；

2016-07-25

航空科学基金(20112108001，2013ZB08001)

邓旺群(1967-)，男，湖南新邵人，自然科学研究员，博士，主要从事航空发动机强度试验和转子动力学研究。