微元法求旋转体体积探讨
2016-12-01梁海滨辽宁对外经贸学院
梁海滨 辽宁对外经贸学院
微元法求旋转体体积探讨
梁海滨 辽宁对外经贸学院
微元法是定积分求平面图形旋转体体积的基本方法,合理选取微元和积分区间是用定积分解决问题的关键。
微元法 定积分 旋转体 体积
前言
定积分的所有应用问题,一般总可按“分割、求和、取极限”三个步骤把所求的量表示为定积分的形式. 可以抽象出将所求量U(总量)表示为定积分的方法——微元法,这个方法的主要步骤如下:
(1)由分割写出微元:根据具体问题,选取一个积分变量,例如X为积分变量,并确定它的变化区间,任取的一个区间微元,求出相应于这个区间微元上部分量的近似值,即求出所求总量U的微元;
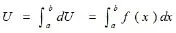
在应用中,旋转体的类型很多,将对几种常见类型的旋转体给予讨论,介绍解决各种旋转体体积的方法。
1.平面图形绕坐标轴所形成的旋转体体积(以X轴为旋转轴为例)
1.1坐标轴是平面图形的一条边
1.2坐标轴在平面图形的外部
取X为积分变量X∈[0,1]
于是,所求绕X轴旋转而成的旋转体的体积



2.平面图形绕与坐标轴平行直线所形成的旋转体体积(以与Y轴平行线X=c为旋转轴为例)
2.1 旋转轴在平面图形的外部(注:无论旋转轴在图形的左侧或右侧微元不变)

2.2旋转轴在平面图形的边上(注:无论旋转轴在图形的左侧或右侧微元不变)
则所求体积为
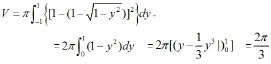

例题略
3.小结
微元法是定积分求旋转体体积的一般方法,但在用微元法求体积时会遇到各种情况。其中旋转轴分为坐标轴和与坐标轴平行情况;旋转轴与平面图形的位置分为内部、外部、边上三种情况。这些类型的关键就是找对积分区间和微元。
[1]吴赣昌.微积分(经济类)[M].北京:中国人民大学出版社,2012-07.
[2]王培吉,王尚户,王嘉谋. 基于微元法旋转体体积的计算[J]. 高师理科学刊, 2010-01.
梁海滨(1978-),女,辽宁人,辽宁对外经贸学院基础课教研部副教授,硕士,从事高等数学教学研究。
