Hybrid control of continuous systems with actuator saturation and state time-delay

,

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)



Hybrid control of continuous systems with actuator saturation and state time-delay

JINGLi,HANShuangwei

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

In controlling of practical systems actuator saturation and time-delay problems often happen. These badly make effects on the stability of systems. Thus systems may face serious accidents. To solve these problems the paper studies the robust stabilization problem of continuous systems with actuator saturation and state time-delay. By introducing auxiliary matrices, control input of the system is limited in convex polyhedron. So the nonlinear saturation function is dealt with into linear function. Hybrid controllers are designed and the closed loop of the system is a kind of switched system. Then single Lyapunov function based approach is used to stabilize it. A numerical simulation is done. The results we get include: a sufficient condition for the stability of continuous system, the switching strategy for the systems under hybrid control. The paper also proposes an estimation scheme of the maximum attraction domain for the system and expresses it into LMI. The results show the method given in this paper is less conservative comparing to convex combination method. The simulation shows a system can be asymptotically stable at the origin in a short time and the domain of attraction is larger.

continuous system; actuator saturation; time-delay; hybrid control

0 Introduction

In practical engineering, systems with actuator saturation or state saturation are common. Saturation function is nonlinear, and the existence of it in the system will cause the system complex and difficult to handle. So research on saturation is important. Since 1990 scholars has studied the saturation problems of continuous and discrete time systems, mainly on the stability and controller design, and achieved fruitful results by using LMI technique. They has also taken into account the partially saturated case[1-2]. State feedback and dynamic output feedback methods have been once used to design the controller[3-5]. In 2001, HU Tingshu used convex combination to deal with saturation part of systems[4], and gave an estimation scheme of attraction domain in 2002[5]. CAO Yongyan (2003), ZUO Zhiqiang (2008) focused on the saturated systems, by using a similar approach they obtained less conservative sufficient conditions of stability and an estimation scheme of attraction domain[6-7]. KAR H and SINGH V proposed a stable condition for discrete systems by utilizing the error existing between variable and its saturation function[1].Systems with saturation and time-delay were also studied. Related researches see references[8-12]. Currently, researches on saturation problems of T-S fuzzy systems and switched systems are being done[13-19].

In 2012, CHEN Yonggang considered the control synthesis problem for discrete-time switched linear systems with input saturation. The convex combination method was used to deal with the saturation nonlinearity and the minimumdwell time approach was used to stabilize the switched system. A state feedback controller and a dynamic output feedback controller were designed, and the domain of attraction of the system was estimated[16]. In 2014, stability and control problem for a class of cascade switched nonlinear systems with actuator saturation was studied[17]. In the paper, the actuator saturation was equivalent to a convex combination formula, and the dwell time approach and the state feedback control method were used to stabilize the system. Reference[18]usedthe antiwindup method to research the control problem of the discrete-time switched system subject to actuator saturation. The paper first designed the dynamic output controllers for the system under neglecting the existence of the saturation. Then antiwindup compensation gains were proposed to maximize the domain of attraction of the system.

The paper analyzes the stability of continuous systems with actuator saturation and time-delay.It first suggests designing a hybrid controller for the system, and the system turns into a switched system. By single quadratic Lyapunov function method the switched system is stabilized. The paper obtains a sufficient condition of stability for continuous system with actuator saturation and time-delay. The paper also proposes an estimation scheme of attraction domain of the system. In the end of the paper a simulation is given.

1 Problem statement

The system model with actuator saturation and state time-delay is described by

(1)

wherex∈Rn,u∈Rm,u=[u1,u2,…,um]T,σ(u) is the standard saturation function.

Define

(2)

where matrixF∈Rm×n,fiis the ith row ofF.

Define

(3)

Definition 2[5]LetV(x,t)=xTPxbe the Lyapunov function of system (1). The ellipsoidε(P,ρ) is said to be contractively invariant if for allx∈ε(P,ρ),

Clearly ifε(P,ρ) is contractively invariant,ε(P,ρ) is a subset of the attraction domain of system (1).

The paper studies the stabilization problem of system (1), which has saturation nonlinearity and state time-delay. The paper uses hybrid control scheme to stabilize system (1).

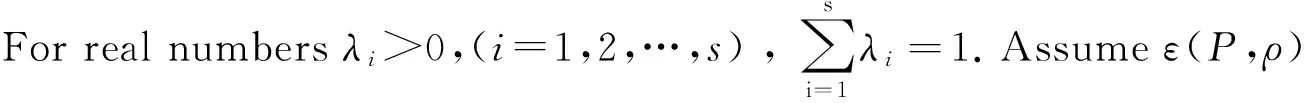
Thecontrollerofsystem(1)canbechosenasfollowing.For∀x∈ε(P,ρ),

(4)

Otherwise,

Further according to the definition of saturation function, formula (2) and (4), the closed-loop system of system (1) is

(5)

So system (5) is a switched system. In the next section the paper uses single Lyapunov function method to stabilize it.

2 Main results

2.1 System stability

In this part we propose the sufficient conditions of stability of system (5), and design the controller of the system.

Let

be the Lyapunov function of system (5).

For ∀x∈ε(P,ρ), ifx∈L(F), the subsystem (5) is active, so

2xT(t)P(A+BF)x(t)+2xT(t)PAdx(t-d)+xT(t)Qx(t)-xT(t-d)Qx(t-d)=

xT(t)(PA+ATP+Q+PBF+FTBTP)x(t)+2xT(t)PAdx(t-d)-xT(t-d)Qx(t-d)=

Suppose

(6)

Assume

(7)

In order to solve inequalities (6) and (7) with LMI Tools, multiply both right and left side of (6) and (7) respectively bydiag(P-1,I). We obtain

LetX=Q-1,Y=P-1,Z=FP-1,Mi=HiP-1, the above inequalities are further rewritten as

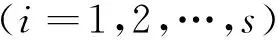
(8)

The above analysis can be summarized into the theorem.

Theorem Consider system (1). If there exist positive definite matricesX>0,Y>0, matricesZ∈Rm×nandMi∈Rm×n(i=1,2,…,s), which satisfy inequalities (8), system (1) is local asymptotic stabilization at the origin under controllers (4).

2.2 The estimation of the attraction domain of system (1)

Define[20]

The estimation problem of the attraction domain of system (1) can be formulated as

(9)

The above optimization problem can be changed into following inequalities problem.

Constraint (a) is equivalent to[5]

Constraint (c) is equivalent to[5]

wherehijis thejthrow of matrixHi, (j=1,2,…,m).

Letγ=α-2,ρ=1 and replaceP-1withY,hijP-1withmij. We obtain the equivalence of (9)

(10)

Problem (10) can be solved with LMI Tools.

3 Simulation

Consider system (1):

Let matrix

We solve the optimization problem (10) with LMI Tools for a feedback with the objective of maximizing the domain of attraction. The result is,

The invariant ellipsoid isε(P,1), see Fig.1.

If we choose (0.9,2)T. as the initial state, the system is asymptotically stable at the origin, see Fig.2.

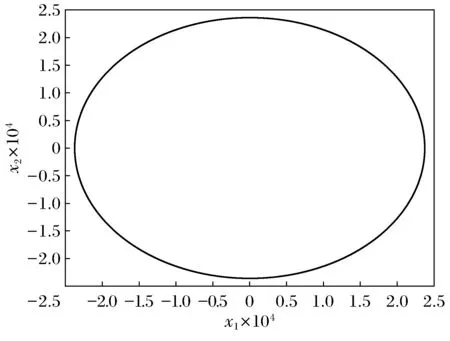
Fig.1 Attraction domain of the system

Fig.2 State response of the system

4 Conclusion

The stabilization problem of continuous systems with actuator saturation and state time-delay is first considered. A hybrid controller is designed and the system is stabilized based on single Lyapunov function method. As a result we propose a sufficient condition of the stability of the system. Then we estimate the attraction domain of the systems. A simulation is given at last to show the effectiveness of the result of the paper.

[ 1 ]KAR H, SINGH V. Stability analysis of discrete-time systems in a state-space realisation with partial state saturation nonlinearities[J]. IEE proc control theory appl, 2003,150(3):205-208.

[ 2 ]SINGH V. Stability analysis of discrete-time systems in a state-space realisation with state saturation nonlinearities: linear matrix inequality approach[J]. IEE proc control theory appl, 2005,152(1):9-12.

[ 3 ]GAO Leifu, LI Xiaoyin. Output feedback stabilization for a class of switched nonlinear systems subject to actuator saturation[C]∥The International Conference of Youth Communication, 2011:231-236.

[ 4 ]HU Tingshu, LIN Zongli. Control systems with actuator saturation: analysis and design[M]. Boston:Birkhäuser, 2001.

[ 5 ]HU Tingshu. An analysis and design method for linear systems subject to actuator saturation and disturbance[J]. Automatica, 2002,38:351-359.

[ 6 ]CAO Yongyan, LIN Zongli. Stability analysis of discrete-time systems with actuator saturation by a saturation-dependent lyapunov function[J]. Automatica, 2003,39:1235-1241.

[ 7 ]ZUO Zhiqiang, WANG Yijing. On enlarging the domain of attraction for linear systems subject to actuator saturation[J]. International Journal of General Systems, 2008,37(2):239-248.

[ 8 ]HONG Xiaofang, WANG Yuzhen. Robust H-infinity filter for a class of uncertain systems with time-varying delay and saturation[J]. Control Theory & Application, 2012,29(2):1245-1252.

[ 9 ]JI Xiaofu, LIU Taihui. Stability analysis and controller synthesis for discrete linear time-delay systems with state saturation nonlinearities[J]. International Journal of Systems Science, 2011,42(3):397-406.

[10]SU Hongye, PAN Honghua, JIANG Peigang, et al. Robust control for a class of uncertain time-delay systems containing nonlinear saturating actuators[J]. Control and decision, 2000,15(1):23-26.

[11]CHEN Dongyan, SI Yuqin. Aysmptotic stability problem for discrete-time delay systems with saturated state feedback[J]. Acta automatica sinica, 2008,24(11):1445-1448.

[12]LI Hui, JING Li. Stability of discrete linear control systems with saturating state[J]. Journal of Shenyang normal university (Natural science), 2012,30(3):331-334.

[13]GAO Xingquan, MA Miaomiao, CHEN Hong. Robust H-infinity controlfor T-S fuzzy systems with time-domain hard constraints[J]. Control theory & application, 2009,26(7):715-721.

[14]TAO Hongfeng, HU Shousong. Robust dissipative tolerant-control of Takagi-Sugeno fuzzy systems with actuator saturation[J]. Control theory & application, 2010,27(2):705-710.

[15]ZHAO Guanglei, WANG Jingcheng. Stability analysis for switched system subject to actuator saturation: an LMI based method[J]. Bulletin of science and technology, 2010,26(5):692-695.

[16]CHEN Yonggang, FEI Shumin, ZHANG Kanjian et al. Control synthesis of discrete-time switched linearsystems with input saturation based on minimumdwell time approach[J]. Circuits syst signal process, 2012, 31:779-795.

[17]WANG Juan, ZHAO Jun. Stability analysis and control synthesis for a class of cascade switched nonlinear systems with actuator saturation[J]. Circuits syst signal process, 2014,33:2961-2970.

[18]ZHANG Xinquan, WANG Mingshun, ZHAO Jun. Stability analysis and antiwindup design of uncertain discrete-time switched linear systems subject to actuator saturation[J]. J Control theory Appl, 2012,10(3):325-331.

[19]ZHONG Guangxin, YANG Guanghong. L2-gain analysis and control of saturated switched systems with a dwell time constraint[J]. Nonlinear Dyn, 2015,80:1231-1244.

[20]HU Tingshu, LIN Zongli. On enlarging the basin of attraction for linear system under saturated linear feedback[J]. System and control letters, 2000,40:59-69.

1673-5862(2016)02-0154-06

具有执行器饱和及状态时滞系统的混杂控制

景 丽, 韩双微

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

实际系统在控制中容易发生执行器饱和及状态时滞问题,这影响系统的稳定性能,给系统带来不可预想的严重后果。为了解决这类问题,研究具有执行器饱和及时滞的连续系统鲁棒控制问题。通过引进辅助矩阵,使系统的控制输入被限制在凸多面体内,系统的饱和非线性函数因而得以处理:采用混杂控制的方法设计了系统控制输入,控制输入与系统构成的闭环系统是切换系统:进一步依据单Lyapunov函数方法镇定系统:最后进行了Matlab数值仿真。提出混杂控制下系统稳定的充分条件及系统切换方案,给出估计系统的最大吸引域方案。结论相比凸组合方法具有较少的保守性,仿真显示所提出的方法可以使系统在较短时间内渐近稳定于原点,且系统具有较大的吸引域。

连续系统; 执行器饱和; 时滞系统; 混杂控制

TP273 Document code: A

10.3969/ j.issn.1673-5862.2016.02.006

过筹学与控制论