一种基于蚁群优化的动态节能路由选择策略

屈 巍, 赵 晶, 洪 洋

(1. 沈阳师范大学 科信软件学院, 沈阳 110034;2. 巴斯大学 科学学院, 巴斯 BA27AY)



一种基于蚁群优化的动态节能路由选择策略

屈 巍1, 赵 晶1, 洪 洋2

(1. 沈阳师范大学 科信软件学院, 沈阳 110034;2. 巴斯大学 科学学院, 巴斯 BA27AY)

针对无线传感器网络中寻找最优路径的问题,考虑网络的节能需求,提出了一种基于蚁群优化的动态节能路由选择策略。蚁群算法在进行过一段时间后,受转移概率公式影响易于陷入局部最优解,因此在提出的基于蚁群优化的动态节能路由选择策略中设计了动态状态转移优化规则,合理的增加了新节点的搜索概率,从而达到快速有效的寻找全局最优解的目的;此外,基于蚁群优化的动态节能路由选择策略设计了奖罚机制,进一步节省搜索时间的同时增加最优路径搜索概率,极大的延长了网络生存时间。仿真实验及分析表明,通过动态状态转移优化规则及奖惩机制的动态调整极大的增加了全局最优解的搜索概率,快速有效地实现了全局最优解的获得,节省了节点能量消耗,有利于延长网络生存时间。

无线传感器网络; 蚁群算法; 状态转移优化规则; 奖惩机制

0 引 言

无线传感器网络由大量具有感知能力、计算能力和通信能力的传感器节点以自组织的方式构成,被广泛的应用于军事及民用领域[1-3]。由于一般工作在无人值守的监控环境中,网络节点电池更换成本较高,因此无线传感器网络的路由设计更多关注于节点能量消耗的最小化[4-9]。出于这些原因,节点在较短的时间内找到最短的路径进行通信不仅利于有效降低节点能耗、延长网络生存时间,也大大提高了无线传感器网络的工作效率,这是目前传感器网络路由设计的一个重要研究方向。由Dorigo M等在1991年首次提出的蚁群算法成为解决此问题的一类典型研究方法,近年来受到广泛研究[10-13]。蚁群算法就是模拟蚂蚁群体觅食行为,后继蚂蚁通过判断前继蚂蚁留下信息素浓度来选择路径。每只蚂蚁根据自己周围的局部环境做出反应并影响于自己周围,单只蚂蚁的行为是随机的,但整个蚁群可以通过自组织过程形成高度有序的群体行为。相同路径上走过的蚂蚁越多,积累的信息量越大,该路径就越容易被选择;信息量会随着走过时间而挥发,走过的时间越久,信息量越小,被选择的概率也就越小。基本蚁群算法就是基于这种自适应机制,使得蚁群算法不需要对所求问题的每一方面都详细认知,而达到从无序到有序的演化。应用在无线传感器网络中,节点不需要对全局节点位置有全部的了解,只需要保存它附近的节点路由,就可以实现整个网络的最佳路径寻径。这大大减少了节点的通信负担,也节省了节点的能量消耗。但基本蚁群算法在实际应用中出现了收敛较快和易于陷入局部最优解的问题,导致全局最优解被忽视[14-15]。本文提出了一种基于蚁群优化的动态节能路由选择策略,通过动态状态转移规则的设计,合理的增加了新节点的搜索概率,快速的实现了全局最优解的获得;通过奖惩机制的合理设计,进一步节省了搜索时间的同时增加了最优路径搜索概率,极大的延长了网络生存时间。

1 基于蚁群优化的动态节能路由选择策略

1.1 相关假设

传感器网络随机部署于二维矩形平面内,使用全向天线,节点的通信半径为Rc,节点感知半径为Rs且Rc=2Rs,从而保证了网络的连通性[16]。若节点i与节点j之间的欧式距离d(i,j)满足d(i,j)≤Rc,则i和j互为邻居节点,可进行直接通信。

1.2 状态转移优化规则

1.2.1 蚁群优化前期概率模型

(1)

(2)

其中: α为信息式因子, 反映蚂蚁在运动过程中积累的信息素对于指导蚁群搜索过程中所占有的重要程度; β为期望启发式因子, 反映在指导蚁群搜索过程中启发式信息所占有的重要程度; ηik(t)为启发函数, dij表示2个邻居节点之间的距离, 该启发函数用于表示蚂蚁k从节点i转移到节点j的期望程度。

为避免残留信息素过多淹没启发信息的情况出现,当m蚂蚁完成对所有n个节点的遍历后,需要对残留信息进行更新。t+tn时刻在路径(i,j)上的信息量调整如公式(3)所示。

(3)

其中:ρ为信息素挥发系数, 1-ρ为信息素残留因子,为防止信息无限积累,ρ的取值范围为[0,1)。Δτij(t)为本次循环中路径(i,j)上的信息素增量,初始时取为0即,Δτij(t)=0。Δτij,k(t)为第k只蚂蚁在本次循环中t时刻残留在路径(i,j)上的信息量,则有

(4)

其中:Q为信息素强度;Lk为第k只蚂蚁在本次循环中走过的所有路径的长度和。

1.2.2 蚁群优化后期概率调整规则

蚁群算法在进行过一段时间后,受转移概率公式影响易于陷入局部最优解。所以,在算法进行一段时间后,应该采取动态扩大转移概率的方法,以便扩大搜索空间,增加找到更优解的几率。

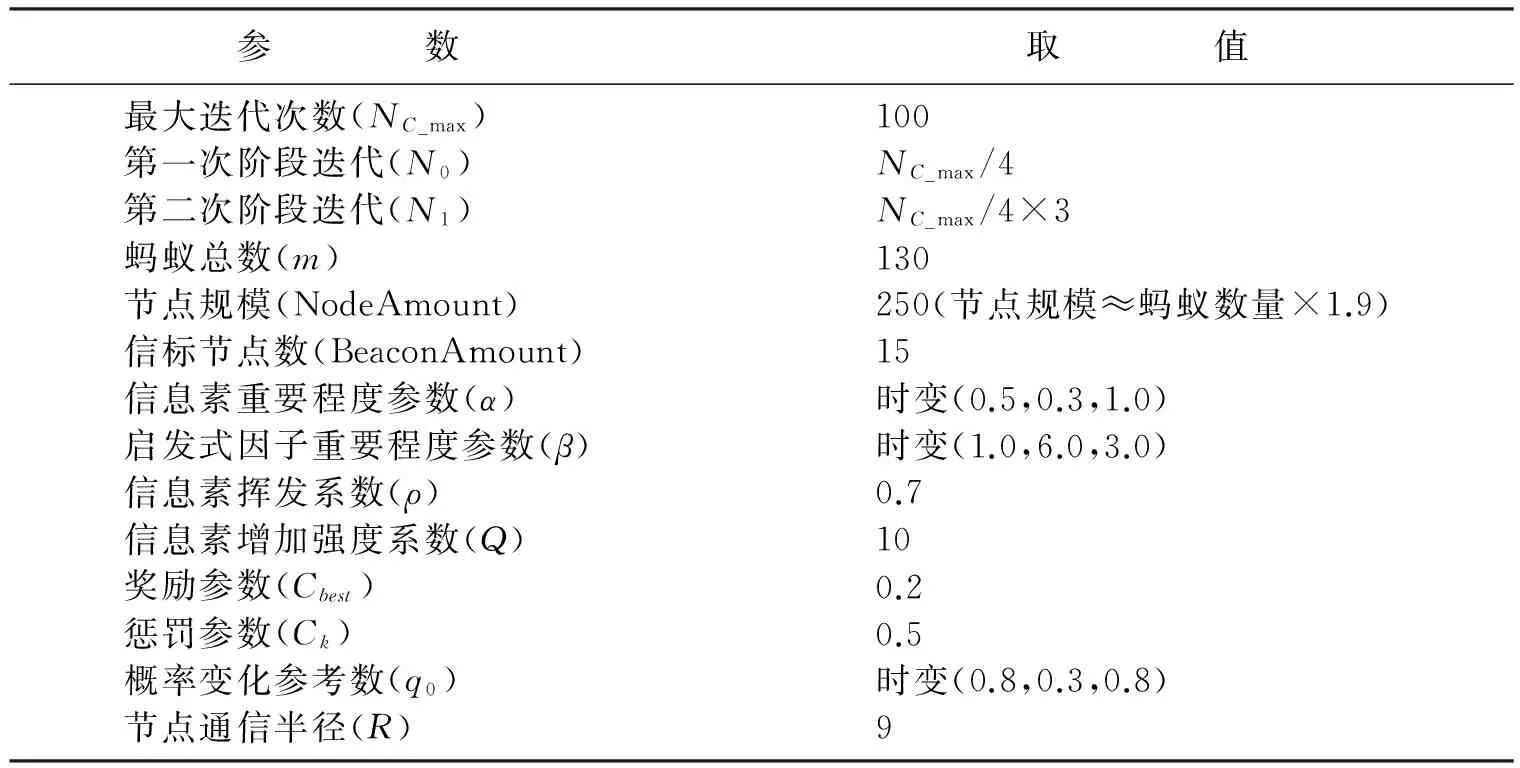
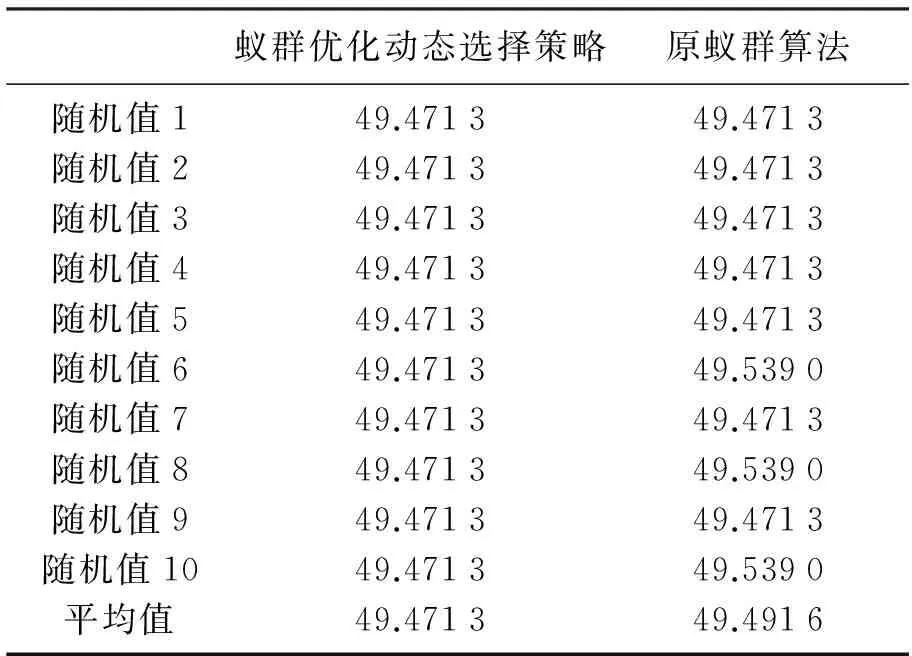
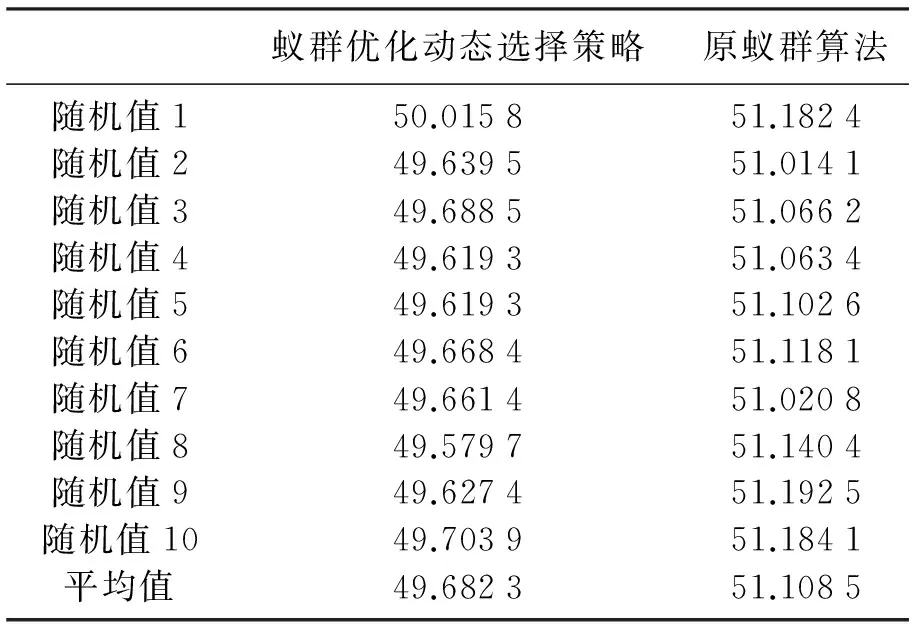
状态转移优化规则首先设计平衡参数q0,以此来平衡“探索”新路径和“利用”己有信息之间的相对重要程度。当q>q0时进行新路径的探索,当q

首先,算法开始运行时,主要以信息素作为选路参考。迭代NC次后,为了防止陷入局部最优解,改变q0值,并设计随机函数rad()产生一个随机数满足rand(min(pij)≤rad≤max(pij)),当pij≥rad时,节点i选择下一跳节点j从而开辟新路径,扩大搜索空间,防止算法陷入局部优化。最后,主要以信息素为参考,再次改变q0值,直到运行结束。

接下来,在α和β方面,状态转移优化规则设计了动态调整,可以有针对性的解决算法易陷入局部最优解的问题。具体地,α反映蚂蚁在运动过程中积累的信息素在指导蚁群搜索过程中的重要程度,α取值不易过大,否则容易导致局部正反馈作用较强,从而导致算法出现收敛过早的现象。

β则反映在指导蚁群搜索过程中的距离的重要程度。β值越大,蚂蚁在局部点上选择局部最短路径的可能性越大,算法极易快速收敛于局部最优,换言之,极易陷入局部最优。

所以,状态转移优化规则设计了根据迭代所在的阶段,动态调整α和β的机制,调整如下:

1) 依据迭代所在阶段来初始化q0、α和β的值。并采用随机函数rad()产生一个随机数赋值给q,且满足0≤q≤1,初始化模型如公式(5)所示。其中,N0为第一阶段迭代次数,N1为第二阶段迭代次数,Nc为当前迭代次数,Nc_max为最大迭代次数,U、U0、U1为时变q0的值。

(5)

2) 当q>q0时,节点i在待选节点集合j[]中随机选择下一跳节点,从而开辟新路径,扩大搜索空间;否则,依据状态转移概率与下一跳由信息素浓度决定。状态转移概率调整模型如公式(6)。

(6)

式中Ln是节点n的邻居节点数。

1.3 奖惩机制

蚁群算法在进行信息素更新时,走过的路径上的信息素会得到一定程度的加强,同时信息素会随着时间的推移不断挥发,因此蚁群算法容易受到早期发现解的影响而陷入局部最优。考虑到以上问题,基于蚁群优化的动态节能路由选择策略设计了奖罚机制,奖励与惩罚规则如下:

1) 当前迭代t=1时,信息素浓度正常更新,即节点间的Δτij(t)在原来基础上进行奖励,即:

(7)

2) 当前迭代t≥2时,记录从开始到上一次为止所有迭代中最短路径长度Lall_best,依据路径长度对信息素浓度实施奖惩。如果当前蚂蚁路径长度Lnow≤Lave[NC](Lave[NC]为当前迭代所有路径平均长度),则节点间的Δτij(t)按照公式(7)进行奖励;如果当前蚂蚁路径长度Lnow>Lave[NC],则节点间的Δτij(t)在原来基础上公式(8)进行惩罚;如果当前蚂蚁路径长度Lnow≤Lall_best,则节点间的Δτij(t)在原来基础上按照公式(9)进行奖励。

(8)

(9)

其中:L(ant)为当前蚂蚁在一个迭代里走完的路径总长;Ck为惩罚参数;Cbest为奖励参数。

1.4 蚁群优化动态选择策略实施步骤

Step 1 确定起始节点S(非信标节点),通过信标节点到未知节点的跳数矩阵找到距离未知节点S最近的一个信标节点D,记录它们之间的跳数为S_hop,并将禁忌表Tabu[]中第一个节点赋值为S,Tabu[]记录m只蚂蚁按次序走过的节点编号。

Step2 NC初始值设置为1,并进行第NC次迭代。

Step 3 第m只蚂蚁寻径开始(m初始值设置为1),禁忌表目前已走过的跳数Tc初始设置为1。

Step4 蚂蚁从节点S开始,将当前已访问的节点放入visited[]中,且初始将visited[]置为目前Tabu[]中第m行1到Tc列的节点的下标。

Step 5 在S的可通信范围内的节点中,把与信标节点D之间的跳数小于S_hop的节点索引下标放入J_tmp[]中。

Step6 在J_tmp[]中选出与S跳数差值最大的节点索引,即最靠近信标节点D的节点索引下标放入j[]中,作为待跳节点的索引。

Step 7 进行蚁群优化的后期概论模型调整,依据公式(5)判断此时的迭代次数是处于初步、中间还是结束阶段。依据所在阶段来初始化q0,α和β的值。采用随机函数rad()产生一个随机数赋值给q,且满足0≤q≤1。

Step8 当q>q0时,节点的状态转移概率p均一样,即在j []中随机选择下一跳节点;否则,依据状态转移调整概率公式(6)进行,即下一跳由信息素浓度大小决定。选好的下一跳放入to_visit中,再将to_visit放入Tabu[]第m行的第Tc++列中。

Step 9 判断to_visit是否为信标节点D。若不是,将to_visit置为S,回到步骤4;若是,将m+1置为m,回到步骤3。

Step10 所有蚂蚁寻径结束,算出每只蚂蚁路径总长L(ant)。

Step 11 记录本次迭代的最佳路径长度,放在L_best[]中。记录本次最佳路径,放在R_best[]中。记录本次平均路径长度,放在L_ave[]中。

Step12 重置本次迭代中的信息素变化矩阵Δτij(t)。

Step 13 在搜索过程中,将发现的路径与本次迭代平均路径长度和以往最优解进行比较,如果优于以往最优解则分别进行不同的奖励,否则进行一定的惩罚。判断当NC=1时,信息素浓度按照公式(7)正常更新,在原先基础上进行奖励;否则,记录从开始到上一次为止所有迭代中最短路径长度Lall_best,依据路径长度对信息素浓度实施奖惩。如果当前蚂蚁路径长度Lnow≤Lave[NC](Lave[NC]为当前迭代所有路径平均长度),则节点间的Δτij(t)按照公式(7)进行奖励;如果当前蚂蚁路径长度Lnow>Lave[NC],则节点间的Δτij(t)在原来基础上按照公式(8)进行惩罚;如果当前蚂蚁路径长度Lnow≤Lall_best,则节点间的Δτij(t)在原来基础上按照公式(9)进行奖励。

Step14 依据信息素更新公式更新信息素矩阵Δτij(t)。

Step 15 禁忌表Tabu[]清零。将NC+1置为NC。

Step16 判断NC是不是大于NC_max。若不是,回到步骤2;若是,迭代结束。

2 仿真实验

2.1 实验数据

采用MATLAB为仿真平台,对所设计的蚁群优化动态路由选择策略下的节点路径选择性能进行验证,仿真实验中各参数取值如表1所示。

表1 参数设置

2.2 蚁群优化动态选择策略与原算法的仿真性能对比

仿真实验中对于蚁群优化动态选择策略与原蚁群算法采用一致的节点分布、相同的起始源节点和终点信标节点。在相同的起始原点与终点信标之间进行路径搜寻,进行了10次独立的随机拓扑实验,分别考察了“最终最佳路径长度”“NC次迭代最佳路径平均长度”和“第一次找到最佳路径的迭代次数”的性能,并针对性能展开重点分析。

表2 最终最佳路径长度性能

表3 第一次找到最佳路径的迭代次数性能

表4 NC次迭代最佳路径平均长度性能

由表2可知,每次实验采用蚁群优化动态选择策略获得的最终最佳路径长度都保持为49.471 3,而原蚁群算法获得的最终最佳路径长度波动较大,可见蚁群优化动态选择策略在最终最佳路径长度方面获得全局最优解的性能较稳定。

图1 NC次迭代中最佳路径平均长度与最终最佳路径长度差别性能

由表3可知,原蚁群算法在10次随机实验下找到最优路径的最短迭代次数为10.3,蚁群优化动态选择策略则为3,可见蚁群优化动态选择策略可以在更短的迭代次数内找到最优解,极大地缩短了搜寻路径的时间,从而有效地降低节点能耗,有利于延长网络生存时间。

由表2及表4可知,2种算法在NC次迭代中最佳路径平均长度与最终最佳路径长度相比均有差距,从具体数值上进行比较,原蚁群算法获得的差距较大,约为1.616 9,采用蚁群优化动态选择策略获得的差距较微小,为0.211,性能比较具体如图1所示,采用蚁群优化动态选择策略获得的差距微小约为原蚁群算法下获得差距的13%。

3 结 语

本文以避免陷入局部最优解、加快搜索速度为优化目标,研究了无线传感器网络中寻找最优路径的问题,提出了一种基于蚁群优化的动态节能路由选择策略,并对其进行了理论分析与实验验证。仿真实验表明,该策略通过动态状态转移规则,有效的增加了新节点的搜索概率,实现了快速有效的寻找全局最优解的目的;通过奖惩机制的设计,节省时间同时进一步增加了最优路径搜索概率,有效的降耗,延长了网络的生存时间。

[ 1 ]QU Wei, LIN Hai, WANG Jinkuan. A dynamic energy-efficient routing scheme in Wireless Sensor Networks[J]. ICIC-EL ,2014,8(11):3113-3119.

[ 2 ]KARIMI M, NAJI H R. Optimize cluster-head selection in wireless sensor networks using genetic algorithm and harmony search algorithm[C]∥20th Iranian Conference on Electrical Engineering, 2012:706-710.

[ 3 ]张国印,唐滨,孙建国,等. 面向内容中心网络基于分布均匀度的蚁群路由策略[J]. 通信学报, 2015,36(6):1-12.

[ 4 ]曲大鹏,王兴伟,黄敏. 移动对等网络中的感知蚁群路由算法[J]. 计算机学报, 2013,36(7):1456-1464.

[ 5 ]AL-ALI R, RANA O, WALKER D W, et al. G-QoSM: grid service discovery using QoS properties[J]. China J Comput, Comput Inf, 2012,21(4):363-382.

[ 6 ]陈志泊,徐孝成. 一种改进的基于跳数的无线传感器网络路由算法[J]. 计算机科学, 2013,40(4):83-85.

[ 7 ]AMALDI E, CAPONE M, FILIPPINI I. Design of wireless sensor networks for mobile target detection[J]. IEEE/ACM Transactions on, 2012,20(3):784-797.

[ 8 ]KARABOGA D, OKDEM S, OZTURK C. Cluster based wireless sensor network routing using artificial bee colony algorithm[J]. Wireless Networks, 2012,18(7):847-860.

[ 9 ]OKDEM S, OZTURK C, KARABOGA D. A comparative study on differential evolution based routing implementations for wireless sensor networks[C]∥Innovations in Intelligent Systems and Applications(INISTA), 2012 International Symposium on, 2012:1-5.

[10]COLORNI A, DORIGO M, MANIEZZO V, et al. Distributed optimization by ant colonies[C]∥Proceedings of European Conference on Artificial Life,1991:134-142.

[11]梁华为,陈万明,李帅,等. 一种无线传感器网络蚁群优化路由算法[J]. 传感技术学报, 2007,20(11):2450-2455.

[12]李领治,郑洪源,丁秋林. 一种基于改进蚁群算法的选播路由算法[J]. 电子与信息学报, 2007,29(2): 340-344.

[13]朱思峰,刘方.柴争义. 一种基于蚁群优化的无线传感器网络路由算法[J]. 北京理工大学学报, 2010,30(11):1295-1300.

[14]杨新峰,刘克成. 基于改进蚁群算法的WSN路径优化[J]. 计算机与现代化, 2012,6(6):102-105.

[15]吴庆洪,张颖,马宗民. 蚁群算法综述[J]. 微计算机信息, 2011,27(3):1-5.

[16]屈巍,李喆. 无线传感器网络中一种分布式冗余检测算法[J]. 小型微型计算机系统, 2010,31(4):577-582.

A dynamic energy-saving routing strategy based on ant colony optimization in wireless sensor networks

QUWei1,ZHAOJing1,HONGYang2

(1. Software College, Shenyang Normal University, Shenyang 110034, China; 2. Department of Science, University of Bath, Bath BA27AY，The United Kingdom of Great Britain and Northern Ireland)

Focus on the problem of finding the optimal path in wireless sensor networks(WSN), and energy saving requirement, a dynamic energy-saving routing strategy based on ant colony optimization(ACO) was proposed . Because of being influenced by the transition probability formula，the algorithm of ACO is easy to fall into local optimal solution after running for a period of time. Thus, in this paper, our strategy designs the optimization rule of dynamic state transformation, which increases the search probability of the new node, so as to achieve the purpose of searching the global optimal solution quickly and effectively.In addition, our strategy introduces the mechanism of rewards and penalties, which further saves the search time and increase the probability of optimal path search, and prolongs the network survival time greatly. Simulation and theoretical analysis showed that the searching probability of a global for the optimal solution is increased by dynamic adjustment of the dynamic state transition rule and the mechanism of rewards and punishments, and the global optimal solution is obtained quickly and effectively. Furthermore the energy consumption of the nodes is saved, and will extend the lifetime of network greatly.

Wireless sensor networks(WSN); ant colony optimization(ACO); optimization rule of dynamic state transformation; the mechanism of rewards and penalties

2015-11-23。

国家自然科学基金资助项目(61403073)。

屈 巍(1982-),女,辽宁铁岭人,沈阳师范大学讲师,博士。

1673-5862(2016)02-0234-06

TP393

A

10.3969/ j.issn.1673-5862.2016.02.022