加速旋转荷电黑洞视界面积量子化

杜 越, 李慧玲

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)



加速旋转荷电黑洞视界面积量子化

杜 越, 李慧玲

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

黑洞视界面积量子化问题是理论物理研究的前沿课题,也是近些年科学讨论的热点问题,现在人们对黑洞视界面积量子化问题等内容进行了一系列的研究,也已经取得了一些成果,但是有一些相关理论的研究还需要深入。通过近视界近似,利用绝热协变量,采用Bohr-sommerfeld量子化原则和黑洞热力学第一定律,研究了不同坐标系下电荷磁荷加速旋转荷电黑洞的视界面积量子化及熵的量子化问题。总而言之,将绝热协变量量子化视界面积推广到对复杂荷电黑洞的视界面积量子化问题的分析和讨论。其核心关键技巧是绝热协变量的方法。最后得到的结果表明,黑洞的面积谱是等间距的,与本身黑洞参数无关。

量子化; 绝热协变量; 面积谱; 荷电加速旋转黑洞

0 引 言

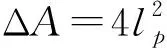
相比于准正规模方法,用绝热协变作用量的方法对带有电荷磁荷黑洞的视界面积进行量子化是方便简单的。在本论文中,由于稳态黑洞的无限红移面与事件视界不重合,也由于角动量的出现,所以时空中存在坐标系的拖曳效应。因此,先做拖曳坐标的转换,然后在绝热协变量的基础上,我们试图得到带有电荷磁荷高速旋转的黑洞的面积谱。

1 有电荷磁荷加速旋转的黑洞

Plebanski等[5]线元覆盖了一大类时空线元,包括熟知的黑洞解如史瓦西黑洞、克尔黑洞、克尔纽曼黑洞、克尔-NUT黑洞等。带有电荷磁荷加速旋转的黑洞也属于这一大类。在球坐标下它可以表达为[6]

(1)

这里

(2)

这里:M是黑洞的质量;a是单位质量角动量;a=J/M;e和g是黑洞的电荷磁荷;α代表的是黑洞的加速度。为了方便,线元可以写成

(3)

这里新的函数可以表达成

(4)

事件视界的定义式为

(5)

内外视界为

(6)

在外视界处,角速度[8]和霍金温度[9]可以写成

(7)

(8)

外视界面积为

(9)

为了避免拖曳效应的影响,做拖曳坐标变换

(10)

带有电荷磁荷加速旋转的黑洞线元可以写成

(11)

这里

(12)

以下采用近视界近似的方法继续对加速旋转的黑洞进行探究,由于现在的方向都更倾向于量子论现象,例如发生在事件视界处的隧穿辐射,黑洞熵和面积谱的量子化,因为临近视界更高维背景的时空可以抵消一个二维时空的影响,所以采取临近视界近似值不会有问题[10],取临界外视任意θ=θ0,线元式(11)可以写成

(13)

当t→-iτ,进行转换

(14)

2 协变作用量

下面用绝热协变量的方法继续对加速旋转的黑洞进行研究,绝热协变量结合加速旋转黑洞的参数可以表达成

(15)

这里:Pi是坐标qi的共轭动量;采取爱因斯坦求和定律,τ是欧几里得时间;qi代表的是类空坐标;Η是系统哈密顿常量;Ic=∫Ldτ,L是Lagrangian作用量。当一个带电粒子隧穿出视界,就会受到电势场的影响,需要考虑到黑洞的物质场问题和黑洞外的电势场。由于存在摇曳效应的影响,临近视界能层中的物质场不能被忽略,但是这里L=Lm+Le,Le=FuV+Fuv/4是电势场的拉格朗日作用量与广义坐标,Au=(Aτ,0,0,0)是一致的,然而从Le可以看出来Aτ是可以忽略不计的,而坐标φ没有出现在拖曳线元中,那也就是说φ也是可以被忽略的。在拉格朗日做用量中,为了去除这2个自由度,经典作用量可以写成

(16)

这里可以得到哈密顿正则方程的表达式

(17)

这里:Ω+是角速度;Φ+是在外视界电磁势能。因此,协变作用量结合黑洞参数可以写成

(18)

3 拖曳球面坐标下荷电加速旋转黑洞的视界面积量子化

(19)

(20)

(21)

将式(20)、式(21)代入式(18)可以得到

(22)

标注一下外视界r+处存在奇点,做一个维道积分[11],将奇点从右向左移。用这种方法,完成对r的积分得到

(23)

根据黑洞热力学第一定律

(24)

再根据Bohr-sommerfel量子化定律

(25)

得到黑洞的熵谱

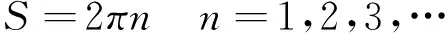
(26)

间隔熵谱

(27)

使用熵和视界面积的关系

(28)

因为已经得到间隔的熵谱式(27),所以根据式(28)可以得到间隔的面积谱

(29)

因此,证明了等间隔面积谱与带电荷磁荷加速旋转的黑洞的参数没有关联。这个结论与Bekenstein最初的结论是一致的。

4 拖曳的Painleve坐标下荷电加速旋转黑洞的面积谱

利用协变作用量表达式(18),继续对带有电荷磁荷加速旋转的黑洞的视界面积和熵谱进行量子化。做painleve坐标变换,令

(30)

即

(31)

将等式(31)代入式(13)中,可以得到带有电荷磁荷加速旋转黑洞在拖曳-painleve坐标下的线元

(32)

通过t′→-iτ′的变换,在线元式(32)中,可以得到测地线方程

(33)

和出入射方程

(34)

(35)

将式(34)、式(35)代入式(18),得到

∫Pidqi=

(36)

在式(38)中右半部分第2小节在拖曳-painleve坐标下没有意义。因此协变作用量可以写成

∫Pidqi=

(37)

根据黑洞热力学第一定律dM=TdS+Ω+dJ+Φ+dQ和Bohr-sommerfeld量子化定律∫Pidqi=nh,发现熵的量子化为

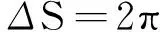
(38)

这也可以算出等间隔面积谱为

(39)

这个结果与本文中第4小节的结果是一致的。也与Bekenstein最初的结论一致。

5 结 论

本文利用绝热协变作用量得到了带有电荷磁荷加速旋转黑洞的面积谱。为了量子化视界面积,首先做了拖曳坐标变换,得到了绝热协变作用量在拖曳坐标下的表达式。然后采用近视界近似,用绝热协变作用量、Bohr-Sommerfeld量子化法则和黑洞热力学定律,成功地量子化了带有电荷磁荷加速旋转荷电黑洞的视界面积。对于黑洞面积谱,在不同的坐标系下,绝热协变作用量给了相同的值,结果显示面积谱是等距的,与黑洞参数没有关系,这个结论与Bekestein最初的结论是一致的。值得注意的是,本论文并没有用似正规模,仅仅通过协变作用量来计算面积谱和熵谱,此方法比似正规模法量子化黑洞更简单。

[ 1 ]HOD S. Bohr’s correspondence principle and the area spectrum of quantum black holes[J]. Phys Rev Lett, 1998,81(20):4293-4296.

[ 2 ]MAGGIORE M. Physcial interpretation of the spectrum of black hole quasinormal modes[J]. Phys Rev Lett, 2008,100(14):141301.

[ 3 ]BEKENSTEIN J D. Black holes and entropy[J]. Phys Rev, 1973,7(8):2333-2346.

[ 5 ]PLEBANLKI J F, DEMIANSKI M. Rotating charged and uniformly acccelerating mass in general relativity[J]. Ann Phys, 1976,98(1):98-127.

[ 6 ]PODOLSKY J, KADLECOVR H. Radiation generated by accelerating and rotating charged black holes in(anti-)de Sitter space[J]. Class Grav, 2009,26(10):105007.

[ 7 ]KERNER R, MANN R B. Fermions tunnelling from black holes[J]. Class Grav, 2008,25(9):095014.

[ 8 ]GILLANI U A , SAIFULLAH K. Tunneling of Dirac particles from accelerating androtating black holes[J]. Phys Lett, 2011,699(1):15-20.

[ 9 ]REHMAN M, SAIFULLAH K. Charged fermions tunneling from accelerating and rotating black holes[J]. JCAP, 2011,2001(3):001.

[10]LI H L, DU Y, ZHENG W, et al. Quantization of horizon aera from accelerating and roating black hole[J]. Int J Theor Phys ,2014,53(7):2349-2359.

[11]李薇. 四维时空中场方程表述形式的推导方法[J]. 沈阳师范大学学报(自然科学版), 2011,29(2):209-212.

Quantization of horizon area from accelerating and rotating charged black hole

DUYue,LIHuiling

(College of Physics Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Issues generated from area quantization of black hole horizon are the frontier of theoretical physics research and as a hot issue of scientific discussion in recent years. At present, a series of researches had been done in order to figure d out the issues of area quantization of black hole horizon, which had also made some achievements. However, there is still some related theoretical researches related theory that needs to be further study. Iin this paper, the issues about complicated charged black hole is discussed. Based on the ideas of adiabatic invariant quantity, and as a further study, adopting near horizon approximation, we attempt to quantize the horizon area of an accelerating and rotating charged black hole in two different coordinate frames. To sum up, based on certain theory, the issues about charged black hole horizon area of quantization have been analyzed and discussed in this paper. The method of adiabatic covariate is regarded as the core key technique that is applied to the practice. Finally, the result shows that the area of the black hole spectrum is evenly spaced, which has nothing to do with black hole itself parameters.

qantization; area spectrum; accelerating and rotating charged black hole; modified adiabatic invariant quantity

2014-12-31。

辽宁省教育厅高等学校优秀人才支持计划项目(WR2013009)。

杜 越(1990-),女,辽宁沈阳人,沈阳师范大学硕士研究生; 通信作者: 李慧玲(1976-),女,辽宁沈阳人,沈阳师范大学讲师,硕士。

1673-5862(2016)02-0206-06

P145.6

A

10.3969/ j.issn.1673-5862.2016.02.017