具约束向量拟均衡问题的Global有效解的最优条件

孟旭东, 陈云龙

(南昌航空大学 科技学院, 南昌 330034)



具约束向量拟均衡问题的Global有效解的最优条件

孟旭东, 陈云龙

(南昌航空大学 科技学院, 南昌 330034)

向量均衡问题是运筹学的重要组成部分,其研究的主要内容包含各种解的存在性、稳定性、连续性、连通性、适定性、最优条件。向量均衡问题的解主要有有效解、弱有效解、强有效解、Global有效解、Henig有效解、超有效解。研究向量均衡问题各种有效解的最优条件是向量均衡问题的一个重要课题。首先,在实Hausdorff拓扑线性空间中引入具约束条件的向量拟均衡问题及其Global有效解的概念;其次,在实拓扑线性空间中分析了锥-凸、几乎锥-类凸与几乎锥-次类凸3种广义凸性的内在关系;最后,在3种广义凸性条件下借助于凸集分离定理给出了具约束条件的向量拟均衡问题Global有效解的充要条件。

向量拟均衡问题; 全局有效解; 向量值映射; 最优条件

众所周知,向量均衡问题理论是运筹学的重要组成部分,向量均衡问题解的最优性条件是向量均衡问题研究中的一个重要课题。因此,不少学者研究了各种向量均衡问题解的最优性条件,见文献[1-5]。Gong[1]在凸性的条件下给出了向量均衡问题弱有效解、Henig有效解、全局有效解以及超有效解的最优性条件,得到了具约束条件的向量均衡问题与不带约束条件的标量化最优性条件等价的结果,并且给出了向量变分不等式以及向量优化问题的各种解的充分必要条件。在凸性的条件下,龚循华等在文献[2]中给出了约束锥内部为空时弱有效解的充分必要条件;在文献[3]中减弱了文献[1]中的凸性假设,也得到了相应的弱有效解的充分必要条件;龚循华等在文献[4]中利用集值映射的切上导数的概念给出了集值向量均衡问题的最优性条件;龚循华等在文献[5]中利用Fréchet可微的概念研究了具约束条件的向量均衡问题的弱有效解、Henig有效解、超有效解以及全局有效解的最优性条件,并在不具任何凸性条件下给出了向量均衡问题的K-T必要性条件,在加上凸性条件下给出了条件的向量均衡问题Heing有效解的充要条件。

1 预备知识

设X为实Hausdorff拓扑线性空间,Y,Z为实局部凸Hausdorff拓扑线性空间。设K为X的非空子集,C,D分别为Y,Z中的闭凸点锥,Y*,Z*分别表示Y,Z的拓扑对偶空间。

记C的共轭锥为C*,即

记C*的拟内部为C#,即

设M是Y的一个非空子集,M的锥包定义如下:

cone(M)={td:t≥0,d∈M}

M的闭包与拓扑内部分别记为cl(M)与intM。凸锥C的一个非空凸子集B称为C的一个基,假若C=cone(B)且0∉cl(B)。显然,C#≠∅当且仅当C有一个基。

设g:K→Z,F:K×K→Y为给定向量值映射,其中F(x,x)=0,∀x∈K。本文考虑以下具约束条件的向量拟均衡问题(简记为VQEPC):找出x∈G,使得

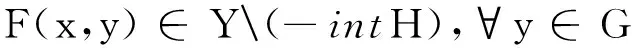
其中H⊂Y为点凸锥,满足C{0}⊂intH,且G={x∈K:g(x)∈-D}。

称满足问题VQEPC的解x为问题VQEPC的Global有效解。

对任何的x∈G,记

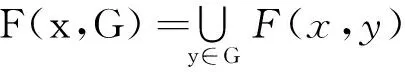
引理[5]设C为实拓扑线性空间Y的凸子集:

1) 则C的闭包clC为凸的。

2) 若intC≠∅,则cl(intC)=clC。

定义[7]设K为X的非空凸子集。

1) 称映射h:K→Y在K上为C-凸，如果对任何的x1,x2∈K,μ∈[0,1]，都有

2) 称映射h:K→Y在K上为几乎C-类凸，如果cl(h(K)+C)为凸集。

3) 称映射h:K→Y在K上为几乎C-次类凸，如果cl(cone(h(K)+C))为凸集。

2 最优性条件

定理 假设以下条件成立:

1)x∈G且B为锥C的基;

2) (F(x,·),g(·))在K上为几乎C×D-次类凸;

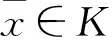
则x为问题VQEPC的Global有效解当且仅当存在y*∈C#,z*∈D*,使得

证明 设x为问题VQEPC的Global有效解。由定义知,存在点凸锥H⊂Y,满足C{0}⊂intH,使得

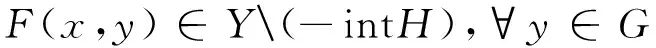
其中G={x∈K:g(x)∈-D},即

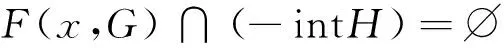
由H⊂Y为点凸锥且C{0}⊂intH,知

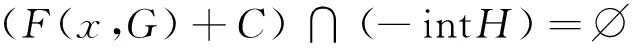
(1)

设P(y)=(F(x,y),g(y)),∀y∈K,则

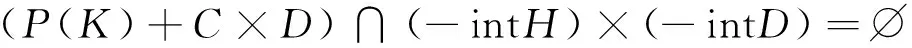
(2)

事实上,假若不然,必存在x0∈K,使得

则

且

(3)

由D为点凸锥知,D+intD⊂D。再由式(3)知,g(x0)∈-intD,从而x0∈G。所以

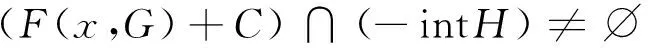
这与式(1)矛盾。

由intH与intD为开凸锥以及式(2)知

cl(cone(P(K)+C×D))∩(-intH)×(-intD)=∅

由P在K上为几乎C×D-次类凸,知cl(cone(P(K)+C×D))为凸集。据凸集分离定理知,存在非零的(y*,z*)∈Y*×Z*,使得

(4)

再由cl(cone(P(K)+C×D))为凸集,知

由(0,0)∈C×D以及P(K)⊂cl(cone(P(K)+C×D)),知

即

(5)

另一方面,由(0,0)∈cl(cone(P(K)+C×D))以及式(4),有

(6)

由intH为凸锥,知对任意的c∈intH以及μ>0,有μc∈intH。据式(6)知

(7)

在式(7)中,令μ→∞,得

(8)

由H为凸锥与intH≠∅以及引理知

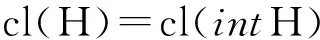
(9)

由y*∈Y*以及式(8)知,y*∈H*。类似可证z*∈D*。

易证明y*≠0。事实上,假若y*=0,则有z*∈D*{0}。再由式(5)知

(10)

(11)

又由x∈G与z*∈D*,知

(12)

由式(11)、式(12),得

(13)

由F(x,x)=0与式(5)、式(13),知

反之,假设存在y*∈C#,z*∈D*,使得

且

由F(x,x)=0与z*(g(x))=0,知

(14)

以下证明x为问题VQEPC的Global有效解。即存在点凸锥H⊂Y,满足C{0}⊂intH,使得

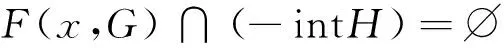
(15)

其中G={x∈K:g(x)∈-D}。

假若不然,则对任何的点凸锥H⊂Y,满足C{0}⊂intH,都有

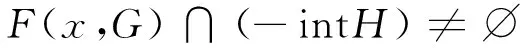
(16)

于是存在yG∈G,使得

(17)

再由C{0}⊂intH以及y*∈C#,知

(18)

又由yG∈G与z*∈D*,知

(19)

由式(18)、式(19),得

(20)

这与式(14)矛盾,因此,x为问题VQEPC的Global有效解。定理证毕。

推论1 假设以下条件成立:

1)x∈G且B为锥C的基;

2) (F(x,·),g(·))在K上为几乎C×D-类凸;

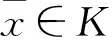
则x为问题VQEPC的Global有效解当且仅当存在y*∈C#,z*∈D*,使得

推论2 假设以下条件成立:

1)x∈G且B为锥C的基;

2) (F(x,·),g(·))在K上为C×D-凸;

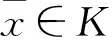
则x为问题VQEPC的Global有效解当且仅当存在y*∈C#,z*∈D*,使得

[1]GONGXunhua,MABochang.Optimalityconditionsforvectorequilibriumproblems[J].JournalofMathematicalAnalysisandApplications, 2008,342(2):1455-1466.

[2]龚循华,孔海星. 约束锥内部为空时向量均衡问题的最优性条件[J]. 南昌大学学报(理科版), 2009,33(3):209-213.

[3]龚循华,熊淑群. 类凸向量均衡问题解的最优性条件[J]. 南昌大学学报(理科版), 2009,33(5):409-414.

[4]龚循华,马博厂. 向量均衡问题的最优性条件[J]. 南昌大学学报(理科版), 2009,33(6):511-517.

[5]龚循华,魏振飞. 向量均衡问题的K-T条件[J]. 南昌大学学报(理科版), 2010,34(5):413-419.

[6]LONG Xianjun, HUANG Yingquan, PENG Zaiyun.Optimality conditions for the Henig efficient solution of vector equilibrium problems with constrains[J]. Optimization Letters, 2011(5):717-728.

[7]DINH T L. Theory of vector optimization(Lecture notes in economics and mathematics systems)[M]. New York: Springer, 1989,319.

Optimality conditions for the global efficient solution of vector quasi-equilibrium problems with constrians

MENGXudong,CHENYunlong

(Science College, Nanchang Hangkong University, Nanchang 330034, China)

Vector vector equilibrium problem is an important part of operations research,including the existence of various solutions, the stability of solutions, the continuity of solutions, the connectivity of solutions, the optimal conditions of solutions. The solution of vector equilibrium problem mainly contains effectivt solution, weak efficient solution, strong efficient solution, Global efficient solution, Henig efficient solution and super efficient solution. Studying optimal conditions of various efficient solutions of vector equilibrium problem is an important topic. Firstly,vector quasi-equilibrium problems with constrians and its Global efficient solution are introduced in real Hausdorff topological vector spaces．Secondly, the inner relations among cone convex, almost cone convex and almost conical sub-convex of generalized convexity are analyzed in real topological linear space. Finally, by using the separation of convex sets, under the generalized convexity conditions, the necessary and sufficient condtions for the Global efficient solution of vector quasiequilibrium problems with constrians are given.

vector quasi-equilibrium problem; Global efficient solution; vector-valued mapping optimality condition

2015-10-15。

国家自然科学基金资助项目(11061023,11201216)。

孟旭东(1982-),男,江西南昌人,南昌航空大学讲师,硕士。

1673-5862(2016)02-0174-04

O317

A

10.3969/ j.issn.1673-5862.2016.02.010