装配网络流最小费用问题

由 巧 俐

(辽东学院 师范学院, 辽宁 丹东 118000)



装配网络流最小费用问题

由 巧 俐

(辽东学院 师范学院, 辽宁 丹东 118000)

讨论装配网络流的最小费用问题。分配网络流和装配网络流是生产网络流的2种特殊简化模型,其中装配网络由4种不同的点构成:用来转运的普通点O-点,用来提供原料的源点S-点,用来收集成品的终点T-点,用来进行装配或合成操作的装配点C-点。在研究装配网络流基本结构及其对偶性质的基础上,定义了一个唯一确定过程来计算原问题的基本可行解和对偶问题的基本解。最后,给出解决该问题的一个网络单纯形法,并对该算法的步骤3如何确定出基变量以及更新基本可行解加以说明。

装配网络流; 最小费用; 基本可行解; 网络单纯形法

Fang[1]提出了一个称为生产网络流的广义网络流模型,并引入了6种不同的点,得到一个生产网络流模型,描述包括多种原材料或产品的生产过程。

本文主要讨论简化的装配网络流最小费用问题,目标是在研究其基本结构及其对偶性质的基础上[1-5],给出该问题的网络单纯形法。其中装配网络流模型主要由用来转运的普通点O-点,用来提供原料的源点S-点,用来收集成品的终点T-点,用来进行装配或合成操作的装配点C-点构成。

1 原问题基本可行解和对偶问题基本解

(1)

(2)

令x是基本可行解,GB是对应于x的基本可行图,如图2,可以得出GB的一些基本性质,如GB可以看作G的一棵支撑树。点s和点t都是活动点[2],且GB是连通的;GB的任意一个圈至少包含一个C-点,对于每个C-点。

图1 转化的装配网络

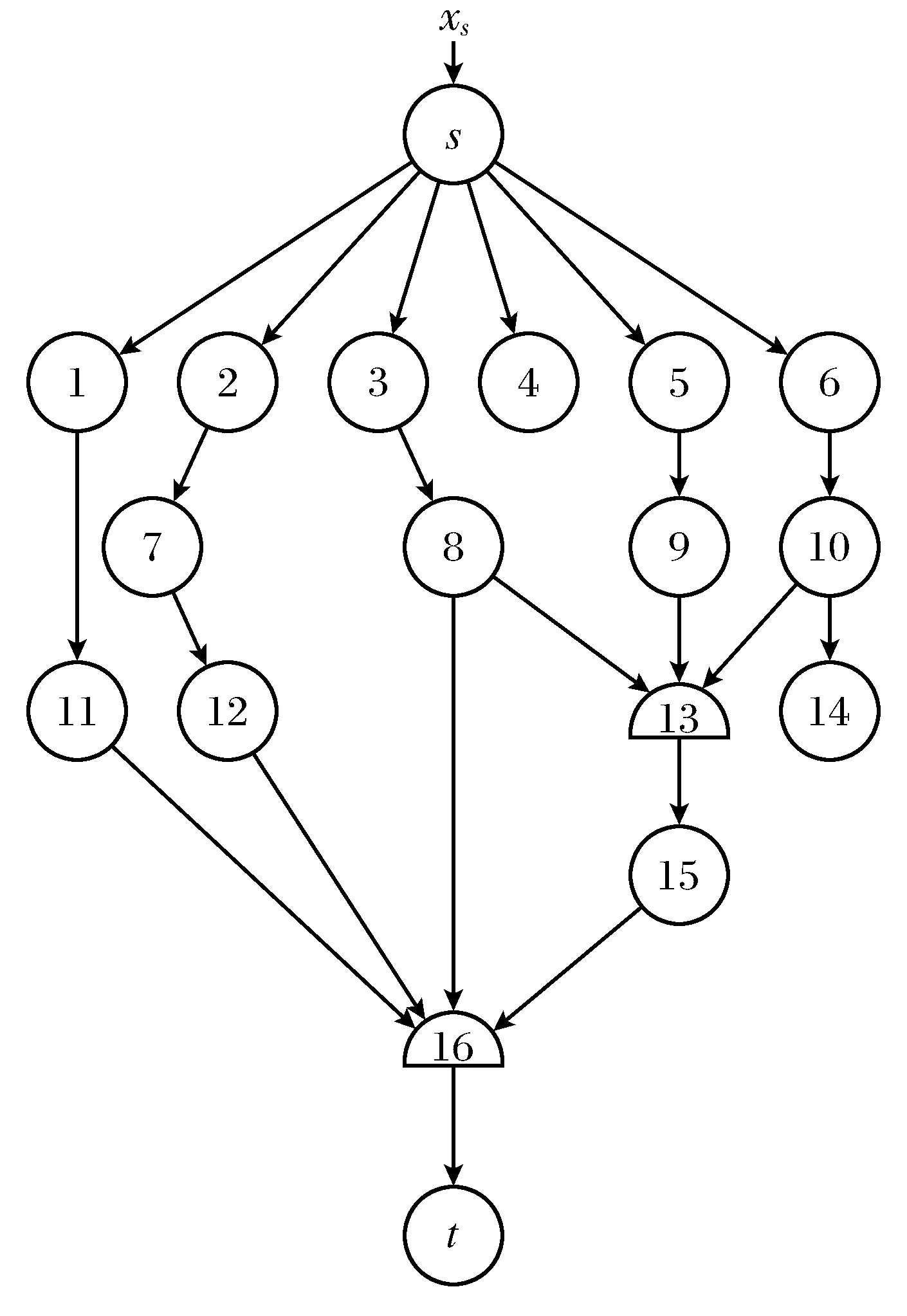
图2 一个基本可行图

最优条件包括3部分:

对于原问题部分,需要满足

(3)

(4)

其中L(i)={i*}

(5)

(6)

(7)

对于对偶问题的基变量部分,需要满足

(8)

(9)

(10)

(11)

(12)

对于对偶问题的非基变量部分,需要满足

(13)

(14)

(15)

(16)

下面是计算原问题基本可行解x的具体步骤。

算法1 令GB是对应于基本可行解x的基本可行图。

步骤1 判断GB的叶子[2]。用式(6)计算与T-点叶子相连的基弧的流值,并置与C-点和O-点叶子相连的基弧的流值为零。

步骤2 判断GB中未计算部分的叶子。用式(4),式(5)和式(6)分别计算C-点,O-点和T-点的叶子。重复该步骤,直到基本可行变量xij全部计算过。

步骤3 用式(7)计算出xs。

定义 在基本可行图GB中,满足下列条件的路叫做可计算路:

1) 路结束于GB的叶子;

2) 同一个点或弧在路中只出现一次;

3) 如果路经过O-点或T-点,则与该点相连的其他基弧开始一些可计算路。

可计算路的定义只用于分析而不是用于实际操作。

定理1 令GB是对应于基本可行解x的基本可行图。则算法1是唯一确定的可计算过程。特别地有:

1) 对于一个非叶子的C-点,与之相连的基弧中只有一条开始一些可计算路;

2) 对于一个非叶子的非C-点,与之相连的基弧中除了一条外全部开始一些可计算路。

证明 令B是GB对应的基矩阵。假设一个非叶子的C-点,与之相连的基弧中有两条弧开始一些可计算路,每一种情况取一个可计算路。由可计算路的定义知,从不在这两条路的每个基弧开始,可以构造另外的可计算路,它们与这两条路在一些非C-点处连接。重复这个过程,直到没有这样的基弧存在,删掉重叠部分,可以看到在这些可计算路中,基矩阵B对应点的那些行是线性相关的,导致矛盾,(1)得证。同样可以证明,对于每个非叶子的非C-点,与之相连的基弧中除一条外全部开始一些可计算路。这些事实保证算法1对应同一个原问题的基变量,不会因为选择顺序不同而产生不同的值。

在计算出原问题的基本可行解后,可以用最优条件(8)～(12)计算对偶问题的基本解。

算法2 令GB是对应于基本可行解x的基本可行图。

步骤1 ys=0。

步骤2 用式(9)～式(12)计算剩余的对偶问题的基变量。可能需要解一些规模小的线性方程组。

定理2 在算法2中遇到的线性方程组的系数矩阵总是非奇异的。

证明 由线性规划的定理可知,在算法2求解过程中,所要解的线性方程组,其系数矩阵是BT,无论怎样把该过程分解成求解较小的线性方程组,只要B是非奇异的,这个过程中遇到的系数矩阵总会是非奇异的。

2 网络单纯形法

利用算法1,算法2及最优条件式(3)～式(16)可以概括一个求解问题(1)的网络单纯形法。

算法3 令GB是对应于基本可行解x的基本可行图。

步骤1 用算法2计算出对偶问题的基本解y和μ。

步骤2 检查对偶问题可行性条件式(13)～式(16),如果都满足,则停止(达到最优)。否则,选择一个破坏对偶问题可行性条件的非基弧(i,j)作为一个新的变量加入基中。

步骤3 换基。将新的基变量加入到当前的基中,找一个基变量出基,并更新原问题基本可行解x,返回步骤1,进行下一次迭代。

算法3的步骤1和步骤2很容易实现,步骤3需要有效的方法去确定出基变量以及更新x。如果知道如何确定旋转图,换基过程可以进一步改进。

如果在步骤2中选择的进基非基弧与一些基弧构成一个不包含任何C-点的圈。可按一般网络旋转过程沿该圈找到一个基弧出基,并更新x。比如在图1和图2中,如果选择非基弧(1,7)进基,则基弧(2,7)将出基。令ω=x2,7,从基中除去(2,7),并给弧(s,1)和(1,7)上的流值增加ω。

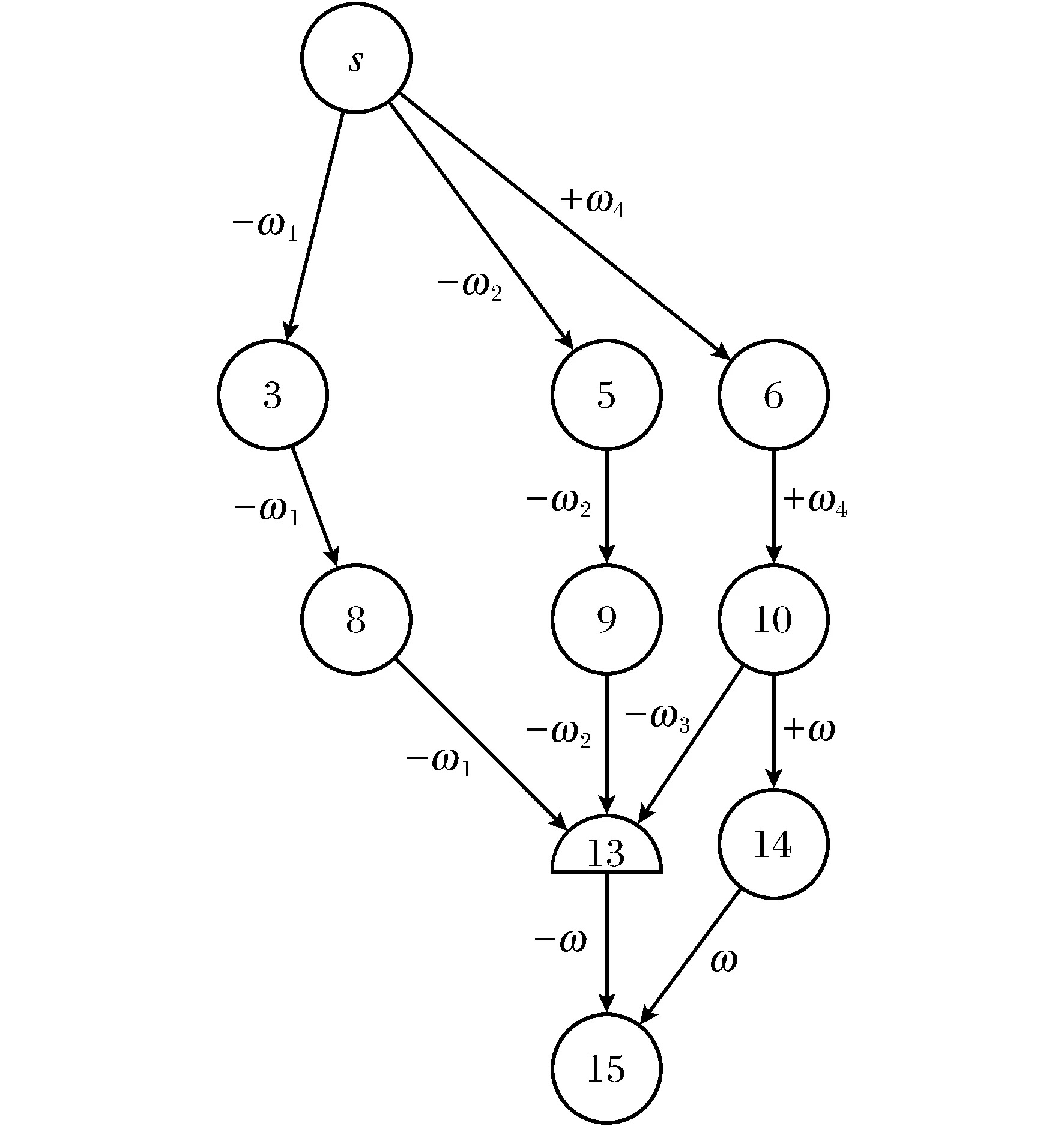
图3 旋转图

另一种情况是在步骤2中选择的进基非基弧与其他基弧构成一个或几个圈,并且每个圈都包含至少一个C-点。死圈在旋转流中无用,因而在确定出基基弧时可以忽略。在非死圈形成的生成图中,如果一些弧是叶子,可以用算法1描述的方法计算这些弧及相关弧上的流值。从生成图中去掉所有错圈和相关点,就可以得到旋转图。如图2中,如果选择弧(14,15)进基,则可得到如图3的旋转图。

在旋转图中,假设进基弧上的流值增加ω,将ω作为一个参数,利用算法1计算旋转图中各基弧上流值的改变量。如图3所示,其中

根据原流值,可以判断出哪个基弧出基。在图3中,随着ω增加x8,13,(13,15),(9,13),(5,9),(10,13)同时到达零,因此可任选一个出基。

在非退化情况下,生成图删掉死圈和错圈后至少剩余一个圈包含进基弧,如果出现不存在出基弧的情况,为使所有弧上的流值之和最小,必须令ω=0,这意味着不应该在步骤2中首先选择该进基弧进基。对于退化情况,可以在GB空闲部分找一个合适的基弧作为出基弧,但旋转图中的流值不发生变化。

3 结 语

本文考虑的是简化的装配网络流最小费用问题,在研究装配网络基本结构及其对偶性质的基础上,给出求解该问题的一个网络单纯形法。

[1]FANGShucheng,QILiqun.Manufacturingnetworkflows:ageneralizednetworkflowmodelformanufacturingprocessmodelling[J].OptimMethodSoft, 2003,18(2):142-165.

[2]胥晓庆,唐恒永. 生产网络流最小费用问题[J]. 沈阳师范大学学报(自然科学版), 2007,25(2):140-143.

[3]LU Haiyan, YAO Enyu, ZHANG Binwu. A note on a generalized network flow model for manufacturing process[J]. Acta Math Appl Sin Engl Ser, 2009,25(1):51-60.

[4]VENKATESHAN P, MATHUR K ,BALLOU R H . An efficient generalized network-simplex-based algorithm for manufacturing network flows[J]. J Comb Optim, 2008,15(4):315-341.

[5]MO Jiangtao, QI Liqun,WEI Zengxin. A netwok simplex algorithm for simple manufacturing network model[J]. Ind Manag Optim, 2005,1(2):251-273.

Minimumcost problem of assembly network flows

YOUQiaoli

(Teachers College, Eastern Liaoning University, Dandong 118000, China)

This paper considers the minimum cost problem of assembly network flows. The distribution and assembly network flow problems are two simplified versions. In an assembly network there are four kinds of different nodes: ordinary nodes(O-nodes )for transition, source nodes(S-nodes) for providing raw materials, termination nodes(T-nodes) for collecting final products, combination nodes(C-nodes) for assembly or synthesis operations. The underlying structure and dual properties of it are specially studied to develop well-defined procedures to compute the primal basic feasible solution and dual basic solution. Finally, we outline a network simplex method for solving this problem. More specially, we show that how to identify a basic variable leaving the basis and to update a basic feasible solution of step 3.

assembly network flows; minimum cost; basic feasible solution; network simplex method

2015-03-09。

辽宁省教育厅高等学校优秀人才支持计划(Lr2013062)。

由巧俐(1980-),女(满族),辽宁东港人,辽东学院讲师,硕士。

1673-5862(2016)02-0170-04

O223

A

10.3969/ j.issn.1673-5862.2016.02.009