关于一类推广的Jacobi恒等式的证明*

宋旭霞

(呼伦贝尔学院数学统计学院，内蒙古海拉尔 021008)



关于一类推广的Jacobi恒等式的证明*

宋旭霞

(呼伦贝尔学院数学统计学院，内蒙古海拉尔 021008)

本文通过对已有Jacobi恒等式结果的研究，推广得出具有不同阶余子式所满足的一类推广的Jacobi恒等式并给出了系统的证明.

推广；Jacobi恒等式；证明

Jacobi恒等式在研究可积系统的精确解的过程当中至关重要，它是运用Hirota双线性方法研究孤子方程结构的基础.一直以来，行列式理论作为矩阵理论的一个分支发展非常迅速，关于Jacobi恒等式及其衍生公式的研究已经得到了比较系统的结果，但Jacobi恒等式中所出现的余子式都是同阶的.我们发现在解决Toda方程的解的问题当中，会出现一类特殊的Hankel行列式，而相关性质的讨论中需要涉及包含阶数不同的余子式的行列式的结构，为此，本文针对此类问题，研究Jacobi恒等式的推广形式.

1 Jacobi恒等式

定理1[1～2]：对于任意的n阶行列式|A|n的代数余子式满足关系式：

2 Jacobi恒等式的推广

Jacobi行列式恒等式中所出现的余子式都是同阶的，如果出现异阶余子式我们可以推广得到下列性质：

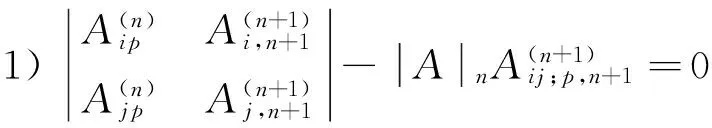
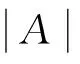
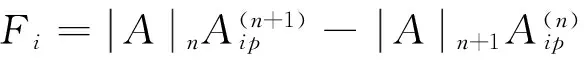
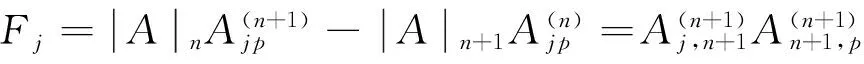
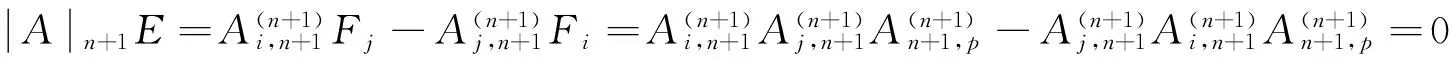
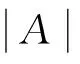
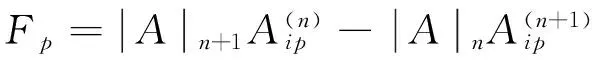
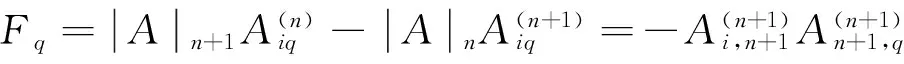
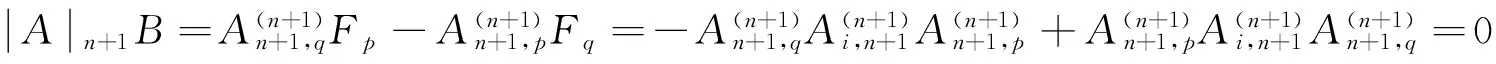
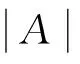
C、作为1)式的特殊情况，令(i,j,p)=(r,n,r)，代入1)式得

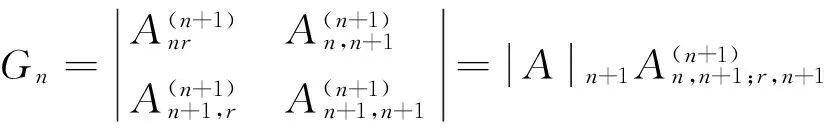
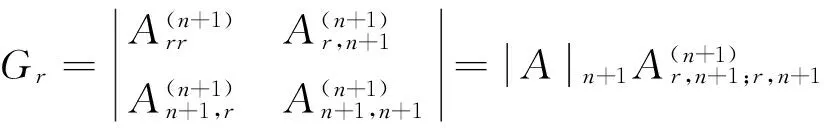
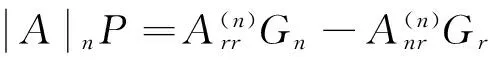
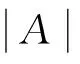
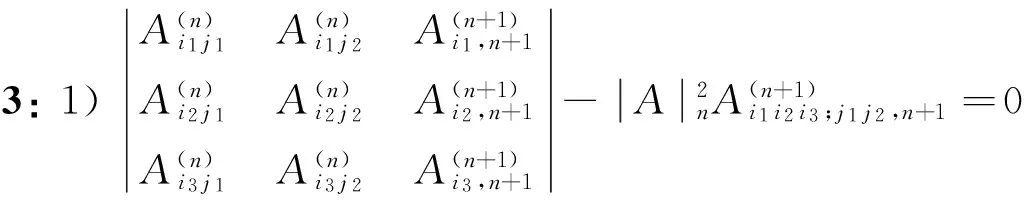
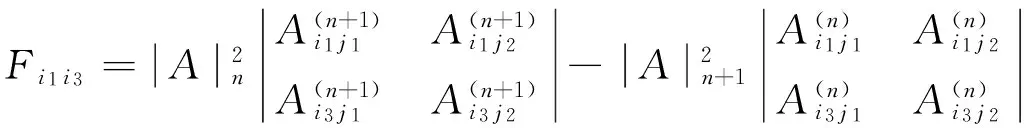
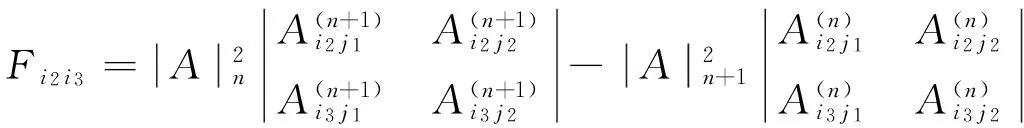
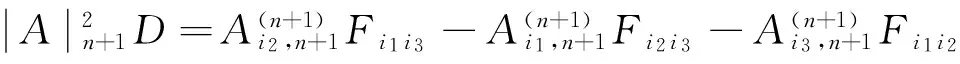
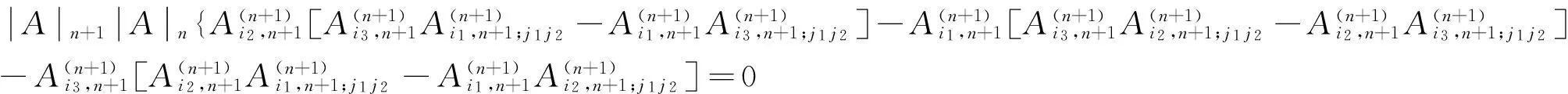
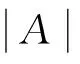
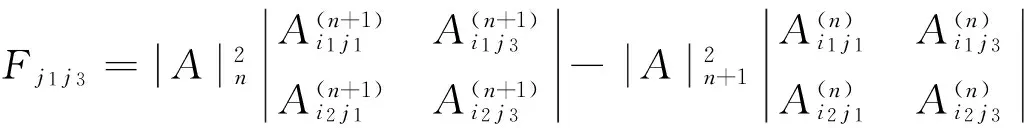
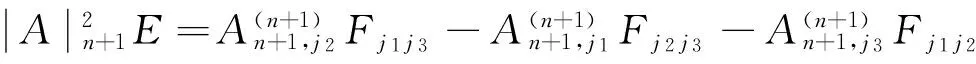
=0

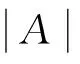
通过文中定理2和定理3的推导，我们得到了推广后的Jacobi恒等式的形式，解决了一类阶数不同的代数余子式所满足的性质.它比Jacobi恒等式本身的应用空间更为广泛，不仅对于研究特殊的Hankel行列式的相关性质有所帮助，更为重要的是可以用它来解决Matsukidaira-Satsuma方程、Toda方程等一系列物理方程的求解问题[3～5]，在可积系统的研究过程中具有一定的应用价值.

[1]Robert Vein，Paul Dale.Determinants and Their Applications in Mathematical Physics [M].Springer-verlag，1998.

[2]胡星标.孤子理论中的直接方法[M].北京：清华大学出版社，2008.

[3]程丽.(3+1)维BKP方程的Pfaff式解Bǎcklund变换[J]. 北京联合大学学报(自然科学版),2012,26(4): 55-58.

[4]王鸿业,温丹华.一个带自相容源的(3+1)维KP方程[J]. 郑州大学学报(理学版),2012,44(4):6-15.

[5]黄丽丽,张金顺. 变系数KDV方程的Grammian解及Wronskian解[J]. 厦门大学学报(自然科学版),2015,54(3):354-357.

On Proof of a Class of Generalized Jacobi Identities

SONG Xu-xia

(School of Mathematics and Statistics, Hulunbeier University, Hailar Inner Mongolia 021008, China)

In this paper, through the study of the existing Jacobi identity, we can get a kind of generalized Jacobi identity which is satisfied by different order and the system is proved.

generalization; Jacobi identity; prove

1673-2103(2016)05-0001-05

2016-08-21

内蒙古自治区高等学校科学研究项目(NJZY250);国家自然科学基金 (11461024); 呼伦贝尔学院重点教学研究项目(ZDKT-026)

宋旭霞(1978-)，女,山东招远人，硕士，副教授.研究方向：微分方程、数学物理.

O151.22

A