基于不定调价次数网络零售配送时隙定价策略
2016-11-30李莹莹陈淮莉
李莹莹,陈淮莉
(上海海事大学 物流研究中心,上海 201306)
基于不定调价次数网络零售配送时隙定价策略
李莹莹*,陈淮莉
(上海海事大学 物流研究中心,上海 201306)
针对客户在线时隙选择具有随机性的特点,网络零售商如何对时效产品配送时隙剩余能力和动态定价联合决策,影响消费者选择行为充分利用配送能力提高整体收益.我们采用同时考虑配送能力与最优定价的方法来研究网络零售配送时隙动态定价策略,此时需求是受时间和价格相互影响的.通过算例分析可以发现,根据Kuhn-Tucker必要条件可以求出动态最优解并找到定价策略,同时在最优解可求出的前提下,根据时效产品特性分析单一降价策略,使得网络零售商收益最大.
配送能力; 动态定价; 不确定需求; 时隙; 时效产品
20 世纪末以来,随着互联网的快速普及和电子商务的迅速崛起,消费者的购物方式发生了很大的转变,由此直接导致线上购物的极速发展[1].随着B2C的发展,电子商务中时效产品出现的频率越来越高,其销售旺季有限(如时尚服装,旺季结束也就过时了;农产品过一定期限会腐烂;体育用品,高科技产品,圣诞物品和期刊).在网络零售商提供送货上门(Home Delivery) 服务的同时随之而来的问题也逐渐增多.时隙(time slot)的概念因此开始引入电商服务中,指网络零售商提供给客户可选择的订单产品送达的交货时间窗[2].目前互联网零售过程中,网络零售商们会在客户下完订单后,提供不同的送货上门服务的配送时隙选项如表1所示[3],客户根据自身情况选择合适的时隙等待订单货物的接收.

表1 某地区某交付日可用的时隙表(部分摘自Peapod.com)
网络零售商提供的配送服务是客户满意程度的重要决定因素,对其成本和收益也有着直接影响.价格在任何商业活动中都扮演很重要的角色.卫亚运[4]在其文章中提到客户分为价格敏感型和交付期敏感型两种类型.关于动态定价策略和收益管理(RM)有大量研究文献,大多数RM问题的研究假设需求函数(价格与需求之间的函数关系)和客户到达率(如泊松过程)对决策者是已知的.这种“全信息”的假设赋予了决策者典型的现实中无法拥有的知识[5].Geunes[3]建立了需求量和需求频率对价格敏感情况下的交付定价模型,以客户区域和价格为决策变量优化收益率.Campbell[6-7]描述了零售商送货服务中的路径和排程问题,并在嵌入启发式算法的基础上建立了求解方案.Lin[8]用仿真评估不同送货策略对网络零售商的影响,重点分析硬时间窗对成本的影响从而均衡配送成本和客户服务水平.Agatz等[2]研究B2C环境下网络零售引入logit效用函数建立价格折扣模型,证明了差异化定价和折扣激励对时隙的短期规划有明显成效.Hamid[9]认为库存系统是时间比例需求的,并建立了启发式求解法确定高质量的订单决策.Hariga[10]开发了一种连续时间库存模型,可以同时适用于增长和衰退的市场.Bose[11]等用线性时变需求项求解确定性库存模型.如果不能充分地了解需求函数,RM问题中定价模型则会采用基本的假设条件,即在合理范围内预测需求[12].然而,标准的预测方法对需求量的历史数据依赖很大,在短生命周期不一定可以获取,如时效产品[13].Kursad[14]将时隙的受欢迎度和价格作为客户选择行为的主要因素建立选择概率公式,因顾客选择动态地调整时隙价格.
传统的时效产品订单配送定价策略中,价格调整的次数是给定的.这就意味着定价决策是在价格调整次数预先设定的假设条件下制定的.现从客户选择行为影响时隙选择订单量,通过不同时隙不同定价影响客户行为充分利用时隙运能优化收益的角度,对时隙配送最优定价策略进行研究.假设任何价格与需求之间的函数关系未知,零售商需要根据之前价格条件下时隙需求决定何时调整价格及面对在线的需求信息如何对应地定价.在实际中,如果价格改变的时间限制在L内(时间越长,调整成本越高),零售商需要在交付期结束之前同时回答两个问题:1)客户要求的配送时隙定价为多少;2)何时调整配送时隙价格.
1 模型构建与描述
1.1 变量与参数说明
1.1.1 集合 TS为配送时隙i选项集合,TS={1,2,…,I},n=0时表示不选择这些时隙选项;BH为客户订单到达时间集合,BH={1,2,…,T};TP为客户订单定价集合,TP={1,2,…,N}.
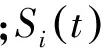
产生的成本;Q为最优的订单量,qi为时隙i客户的订单量.
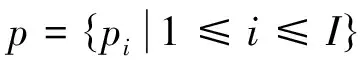
1.2 基本模型
建立的模型只针对时效产品,因为时效产品有其独特的性质,具有一定的期限,必须在期限内完成订单否则产品将无价值.假设在时隙i有客户购买时效产品的配送需求,网络零售商需在交付期L内完成客户的配送需求,订单的需求是受时间和价格相互影响的,由此建立需求模型:
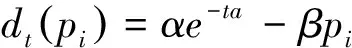
(1)
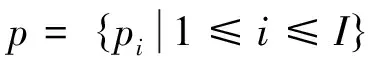

图1 配送时隙的交付期Fig.1 Lead time of time slot
假设客户订单处于第n次定价时相对应价格为pn.时隙i表示时间间隔[(i-1)T,iT]其中T=L/N表示任意两次价格变动的时间间隔.Ei表示截止到时隙i已消耗的配送能力.则
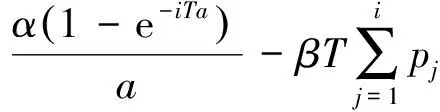
(2)
s.t. D_i≤Ei≤Di,∀1≤i≤n,
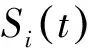
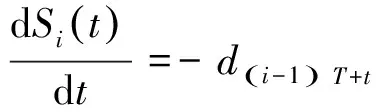
(3)
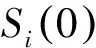
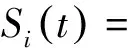
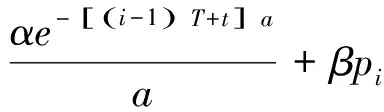
(4)
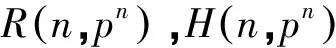
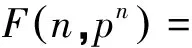
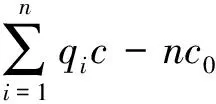
(5)
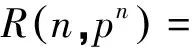

(6)
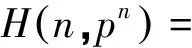
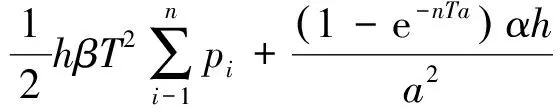
(7)
需要注意的是时隙的剩余配送能力为零,即交付期内每个时隙的订单量qi所需配送能力等于时隙i的配送能力Di,因此客户订单量预测为时隙能够配送的最大量.由此方程(2)可以改为
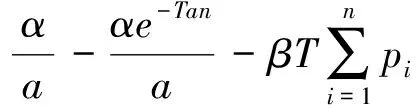
(8)
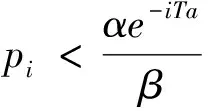
(9)
n≤Nmax,
(10)
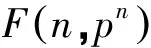
2 模型理论验证
这部分我们将用理论证明可以找出最优N,Pn.所求利润方程则是包含n,p的复合函数,其中n是离散变量,P是连续变量.对于不同的n值,下列约束问题表示为Kn:
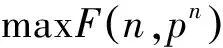
(11)
为找出最优解,对问题建立拉格朗日函数

(12)
对所有时隙i,作为Kuhn-Tucker必要约束条件λis,λi≥0.(Kuhn-Tucker条件是一个非线性规划(Nonlinear Programming)问题有最优化解法的必要和充分条件.这是广义化拉格朗日乘数的成果.)
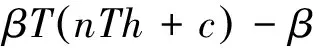
(13)
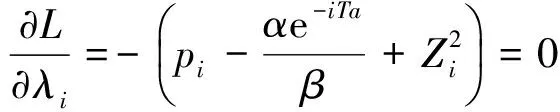
(14)
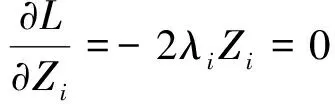
(15)
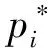
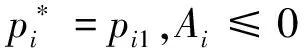
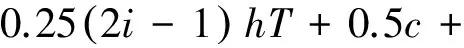
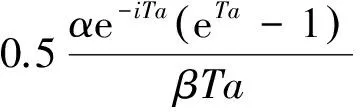
(16)
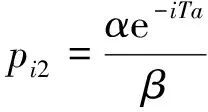
(17)
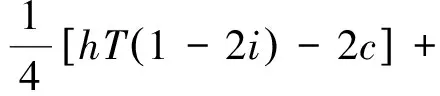
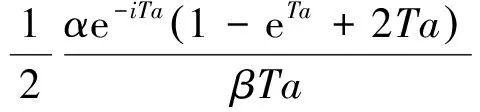
(18)
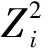
3 算例分析
在第2部分已经证明模型可以找出时效产品配送时隙的最优定价策略,算例分析部分首先用具体数据来分析动态定价与静态定价策略下的企业收益.另外还将从需求量角度做分析如下:假设每位顾客对配送时隙有一个预留价格,即对时隙定价所能接受的价格fi,fi在封闭区间 [f-,f-]内.假设高预留价比低预留价的时隙更受客户欢迎(以下简称为high before low,HBL问题),此时给定一个线上定价策略的上限并提出与之相符的一个竞争率,由此获得最优在线策略,解决何时调整价格及涨价或降价多少的问题.
3.1 为验证模型的正确性和有效性
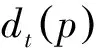
根据不同n值,∀i≤n,用程序算法可以得出结果如表2.

表2 例1解
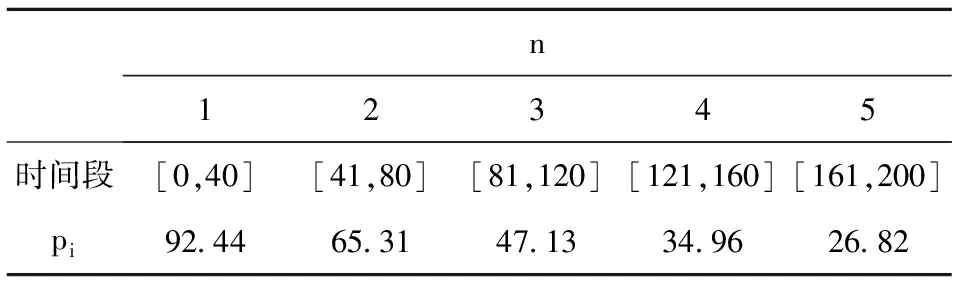
n12345时间段[0,40][41,80][81,120][121,160][161,200]pi92446531471334962682
从表2可见当n=5时取最大利润160 353,相应的订单量是3 313.3.
从表2还可得出静态定价策略(n=1)的最大利润是140 331,对比动态定价策略,可以发现动态定价策略可使利润更大化.
3.2 竞争分析
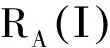
为简化问题,只处理较高预留价格比较低预留价格时隙更受欢迎的问题(为方便以下简称HBL).首先为这个问题设计了一个在线降价策略,然后给出一个适用于任何策略的上限.如果所提出策略的竞争率与上限相符,则意味着此策略最优.


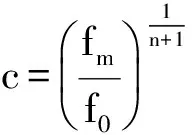
证明 考虑任何需求I实例:应用在线控制策略,R为总收益,令R*为采用最优线下策略的总收益.从在线算法和竞争分析角度,假设竞争对手会根据在线策略尽可能地使客户的时隙需求量最小.但无论需求量如何,当在线策略制定者设定与f0相等的初始价格时,只会面对两种可能的情况:(1)交付期内所有时隙以f0价格被客户全部选择;(2)仍有一些时隙有剩余配送能力,即预留价格大于等于f0的客户订单所需的配送能力小于Di.然后我们将根据实例证明定理.
情况 1. 所有时隙以f0价格被客户选择.在这种情况下,价格和配送能力的上限分别是f0和Di,则收益R=Dif0(订单量需配送能力单位值为1) .因此,线下策略收益最多为Dif0,此时的竞争率:
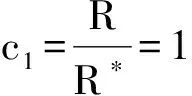
(19)
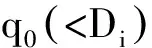
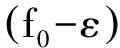
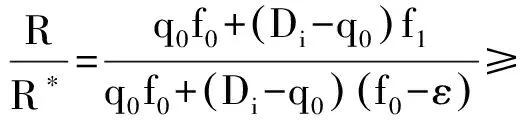
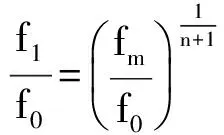
(20)
情况2.2. q1 (21) 情况2.2.2. q2 接着上述情况分析,最多有(n+1)种可能性.在第i(1 ≤i ≤n)种情况,始终会有剩余时隙未被选择,直至价格降至fi.在第(n+1)种情况,尽管价格降至fn,仍会有剩余时隙,剩余配送能力,所以零售商需要以最低价格fm为剩余时隙定价. 根据上述情况分析,得到对于第i(1 ≤i ≤n)种情况,在线策略和最优线下策略收益率等于 (22) (23) 3.2.2 上限 (6) 证毕. 文章研究电商环境下网络零售商提供时效产品配送,配送时隙定价策略.根据客户的时隙选择行为具有随机性的特点,分析客户选择行为的影响因素,建立定价模型.在定价时间和价格相互影响较大的情况下,用价格吸引客户选择时隙,使得时隙剩余配送能力为零.在算例分析中用数据表明动态定价相比静态定价的优势,另外,从时隙需求量角度分析,网络零售商如何使用降价策略影响客户行为让剩余配送能力为零,充分利用已有配置资源增加收益. 在今后的研究中,可以从配送服务和客户满意度多目标规划方面入手,考虑不同客户满意度对订单量的影响,配送服务对于客户满意度如何影响,充分配置运载能力.这样可以更好的提高网络零售商的配送服务质量,使之更有效率,收益更高. [1] RESEARCH F. Topic overview: US online retail[EB/OL].https://www.forrester.com/seareh. [2] AGATZ N,CAMPBELL A. Time slot management in attended home delivery[J]. Transportation Science,2011,45(3): 435-449. [3] GEUNES J,MAXSHEN Z J,EMIR A. Planning and approximation for delivery route based services with price-sensitive demands[J]. European Journal of Operational Research,2007,183(1):460-471. [4] 陈淮莉,卫亚运. 基于客户选择行为的网络零售配送时隙定价模型[J].安徽大学学报(自然科学版),2014,38(3):7-9. [5] BESBES O,ZEEVI A,Dynamic pricing without knowing the demand function: risk bounds and near-optimal algorithms[J].Oper Res 2009,57 : 1407-1420. [6] CAMPBELL A M,MARTIN W P,SAVELSBERGH A. Decision support for consumer direct grocery initiatives[J]. Transportation Science,2005,39(3):313-327. [7] CAMPBELL A M,MARTIN W P,SAVELSBERGH A. Incentive schemes for attended home delivery services[J]. Transportation Science,2006,40(3):327-341. [8] LIN I,MAHMASSANI H S. Can online grocers’ delivery some logistics considerations[J]. Transportation Research Record,2002,1817(3):17-24. [9] HAMID B K. Replenishment schedule for deteriorating items with time-proportional demand[J]. Opl Res Soc,1989,40(1): 75-81. [10] HARIGA M A. Effects of inflation and time-value of money on an inventory model with time-dependent demand rate and shortages[J]. Eur J Opl Res,1995,81(3): 512-520. [11] BOSE S,CHAUDHURI K S. An EOQ model for deteriorating items with linear time-dependent demand rate and shortages under inflation and time discounting[J]. J Opl Res Soc,1995,46(6): 771-782. [12] MCGILL J I,RYZIN G J. Revenue management: research overview and prospects[J].Transp Sci,1999,33(2) 233-256. [13] KURAWARWALA A A,MATSUO H. Forecasting and inventory management of short life-cycle products[J]. Oper Res,1996,44(1):131-150. [14] ASDEMIR A,JACOB V S,KRISHNAN R. Dynamic pricing of multiple home delivery options[J]. European Journal of Operational Research,2009,196(1): 246-257. Dynamic pricing of delivery time slot for online retailing with uncertain price setting LI Yingying,CHEN Huaili (Academy of Scientific Research,Shanghai Maritime University,Shanghai 201306) As the randomness of time slot for customers’ online choice behavior, online retailers’ decision combing the delivery time slot and dynamic pricing will affect consumers’ choice and promote the overall benefit through full use of delivery capabilities.In order to find the dynamic pricing strategy of time slot for online retailing delivery, the delivery capacity and optimal prices are investigated together under the condition that demands is dependent on time and price. The analytical results show that a pricing solution is able to generate from the Kuhn-Tucker necessary conditions. Then according to time-sensitive product feature, the profit of online retailers is maximized based on the optimal solution. delivery ability; dynamic pricing; uncertain demand; time slot; time-sensitive product 2015-12-30. 上海市哲学社会规划课题资助项目(2014BGL018);国家社会科学基金项目(15BGL084). 1000-1190(2016)05-0677-06 F252.21 A *E-mail: lyy2015525@outlook.com.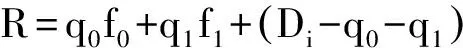

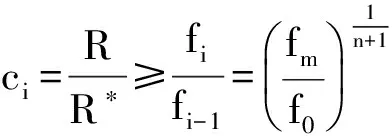
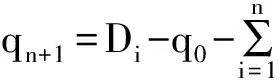
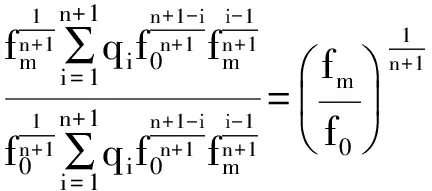
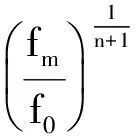
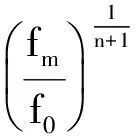
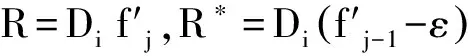
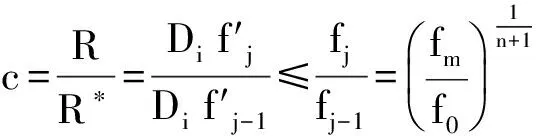
4 结束语
