基于悬链线模型的深水海光缆敷设技术研究*

柯 超，王瑛剑，张鹏杨

（海军工程大学，湖北 武汉 430033）

基于悬链线模型的深水海光缆敷设技术研究*

柯 超，王瑛剑，张鹏杨

（海军工程大学，湖北 武汉 430033）

海光缆的敷设质量直接决定海光缆系统的使用寿命。介绍海光缆深水定余量敷设与浅海定张力敷设的区别，比较两种控制模型的适用性，同时简要介绍相对成熟的定余量敷设直线模型及其应用，并在此基础上分析直线模型的局限性，提出了基于悬链线的深水敷设模型。其中，重点分析了下坡敷设的情况，得出了此地形条件下敷设海光缆长度与船只行驶距离的关系，即布缆速度与船速的关系。这将对深海布缆控制提供参考。

深水海光缆；定余量敷设；直线模型；悬链线模型

0　引 言

海光缆的敷设施工是海缆工程的重要环节，其敷设的质量直接决定海光缆系统的使用寿命。深水海光缆定余量敷设有别于浅海定张力敷设。由于深海地形的复杂程度明显高于浅海，使得深海敷设成为整个敷设施工的难点。原有的直线模型在慢速敷设湿设备和URADUCK套管情况下将不再适用，因此本文提出了悬链线的深水敷设模型，并重点分析了下坡敷设的情况。

1　定余量敷设与定张力敷设

海光缆的敷设按海区不同，可分为铺设和埋设两种作业方式。铺设一般在深水区域进行，即把海底光缆直接铺在海底上；埋设一般在浅海区域进行，是把海底光缆埋在海底面下，埋设深度需根据施工海域确定[1-2]。

海缆的敷设控制方式分为定余量控制和定张力控制。

1.1定余量控制

所谓定余量，即布缆的实际长度（L）大于敷设路由长度（l），这个多余的海缆长度对于路由长度的百分率称为敷设余量（S），即S=[(L-l)/l ]×100%。

实际施工中，余量的多少根据海底坡度、水深等因素确定。通常，海缆敷设余量随水深、海底坡度的变化在1%～5%之间变动。在海底比较平坦、坡度不大的海域，有1%～2%的余量就足够保证海缆服帖地敷设在海底。

1.2定张力控制

按照敷设海区水深和海缆在水中的重量，计算出海缆敷设的张力作为布缆控制的依据。布缆时，观测力计显示的张力值，调整布缆机械的制动力，达到定张力布缆控制。实际施工中，定张力布缆时，布缆机是被海缆拖着被动运转的。因此，布缆机的速度取决于船速，布缆机仅起着制动作用。

理想的张力情况是海缆达到海底着底点时张力等于零，则船上的海缆张力T大体上相当于船与接地点之间的海缆的水中重量，即T=W×H，其中W为海缆的水中重量（kg/m），H为水深（m）。但实际上，布缆时海缆还要受到流速等流体的影响。此外，海缆与海缆通道、测力测速装置、滑轮组之间的摩擦，还有海缆从缆舱提升至舱口等，对张力都存在一定的影响。当然，这些影响比较小，计算也比较复杂。根据经验，需要额外加上200 kg作为控制张力，即T=W×H+200。这样可以使海缆在着底点保持适当的残余张力，有利于保护海缆。

1.3两种敷设方法的区别。

定张力法，即在施工设备上设定一个张力值，如果施工设备检测到海缆的张力值超过了设定的张力值，就会释放海缆。由于这种方法需要设定张力值，而海缆的张力会随着海底地形的不断变化而改变，因此这种控制方法主要用于浅海敷设。因为浅海的地形较为平坦，通常为1°到5°，这样施工设备上设定的值就不会经常性改变。海底光缆深海的敷设，通常是在船尾部布缆，采用余量控制的方式。这种方法作为海缆敷设中的主要手段，是目前国内外通行的深海布缆的唯一方法。定余量控制方式是一种主动布放的控制方式，其关注的重点在于船速和布缆速度的配合。由于船速不会经常改变，因此为了适应不同的海底地形，需要及时调整布缆的速度，以达到需要满足的余量条件。

1.4两种敷设模型的比较

定张力控制的敷设模型，其控制变量是张力，即根据设定的张力作为判断门限。由于船速的变化不宜过于频繁，因此定张力控制模型的因变量即为布缆的速度或者缆的长度。如果深海敷设采用定张力控制，将会出现非常棘手的情况。首先，深海地形的变化十分复杂，上下坡较为频繁，且坡度较大，如果将固定的张力值作为控制参量，则必须频繁改动门限；其次，由于深海的层流分布很复杂，同时悬于施工船只和着底点的海缆长度非常长，因此海缆受到洋流的作用比较明显，即张力的跳动非常频繁，使得定张力控制的门限设置难以确定。这也是定张力控制只限于浅海敷设的原因。

定余量控制的敷设模型，其控制变量是布缆的速度。它是根据轮胎机或者鼓轮机的运转速度来决定的。同样，定余量控制也不适宜对船速进行频繁调整。因此，定余量控制模型的因变量是缆的张力。海缆拉力分为破断拉力（UTS）、瞬间动态拉力（NTTS）、最大工作拉力（NOTS）、静态拉力（NPTS）等四类相互关联的数值[3]。海缆工作拉力是海缆施工中允许加在海缆上的最大拉力，通常取海缆破断拉力的1/3。海缆瞬态拉力是允许加在海缆上的最大拉力，通常取海缆破断拉力的1/2。实际施工中，海缆的拉力只是作为一个参考量，其大小可以通过张力计测量出来。通常，它的值会比海缆的工作拉力小。当海缆在其允许的最大水深敷设时，有可能达到海缆的工作拉力，甚至达到瞬态拉力。但是，海缆的张力设计通常会有很大的富余，且最大水深区段通常也只占整个路由的很小部分。因此，海缆的张力很少情况会处于危险的境地。换句话说，定余量控制，只需要以合理的速度布放海缆，就能够实现安全的敷设。

2　定余量敷设的几何模型

2.1直线模型及其应用

定余量敷设直线模型[4]基于如下假设：在没有海潮流且海底地形又完全平坦的简单状况下，敷设船以一定的速度航行，并以不低于船速的速度敷放电缆。由于电缆各个部分以一定的速度下沉，从船到着底点间的电缆成一直线的形状，接地点的电缆张力为零。敷设中，作用于正向海中落下的电缆各部分的力，有阻碍电缆向其法向和切线方向落下的水的阻力、重力和敷设船的牵引力。因为每个单元长度电缆的各部分不存在加速度，所以作用于这些部分的法线和切线方向的力的和为零。

定余量敷设直线模型在各种海底地形中的应用（此处无底部余量Bottom Slack）：

同等水深条件下敷设时，有：

式中，Vc表示布缆速度，Vs表示船速。

（2）坡度下降和上升时，有：

式中εs称为电缆余量，表示放出多余电缆的速度对船速的百分率；α是电缆的入水角，β是坡度角。

（3）改变船度时，有：

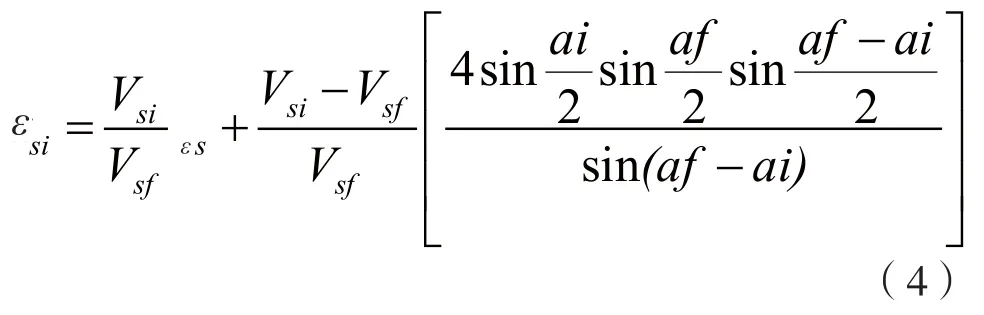
式中εsi称为过渡余量，表示船从船速Vsi变换到Vsf，且确保电缆余量εs所需要追加的余量；ai表示船速为Vsi时的入水角；af表示船速为Vsf时的入水角。

2.2直线模型的局限性和改进

如果电缆的送出速度慢于船速，电缆的接地点就会出现张力，电缆的形状就成了向海面凹状曲线，这就是目前海缆界公认的悬链线[5-6]。参考文献[3]中更是提到，当布缆速度Vc不等于船速Vs时，悬于船只和着底点的海缆形状接近于悬链线。但是，这并没有数学理论的支撑。因为就水动力原理而言，不同的布缆速度下，海缆会有不同的入水角。虽然着底点可能会有距离上的偏移，但是海缆在水中的形状仍然有可能是直线。根据马凯海洋工程有限公司提供的资料显示，海缆在水中敷设时，并不会在船与着底点之间存在多余的海缆，即海缆呈直线。参考文献[5]和参考文献[6]中都提到了海缆船处于静止状态时海缆船的悬链线模型。在此基础上，可以假设：如果船速非常慢，以至于接近静止状态，那么此种状态下的海缆形状呈悬链线型。

在实际施工中，这种情况是有可能出现的。例如，在海缆经过坡度非常大的断崖或者不同缆型交越时，需要安装URADUCK套管，此时船速非常慢，通常航行的速度与布缆的速度保持一致，数值为0.1～0.25 km/h。再如，中继器和接头盒等设备的布放。由于此类设备需要精密地布放，所以布放的速度也很慢。那么这种情况下，海缆的形状大致呈悬链线状。

静止状态时，海缆的形状呈悬链线，以最低点为原点建立坐标系，则其方程为：

式中TD是海缆落地点张力（N）；q是海缆在水中每米的重量（N/m）；x,y是海缆上任意一点M的坐标（m）。

海缆弧线长度L的方程为：

任意点处的受力平衡方程组：

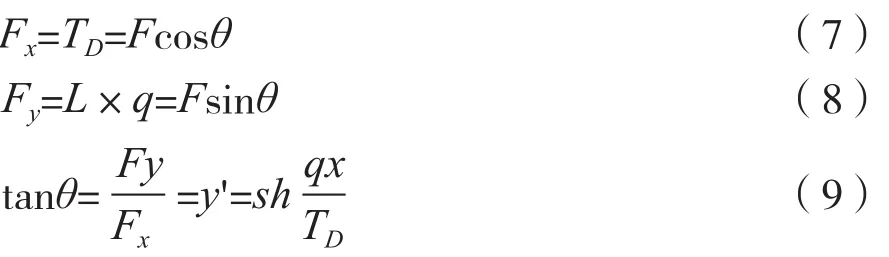
式中Fx、Fy分别为(x,y)处张力F的水平分量、垂直分量；L为最低点到(x, y)处的缆段长度；θ为坐标(x, y)处的切线角。

中继器和接头盒的布放通常考虑在地势较为平坦的地方，那么可以把海底地形看成理想的平底。在不考虑洋流作用和湿设备对海缆重量分布的影响下，海缆在海水中的整个布放过程中都呈悬链线型。由于船速和布放速度几乎一致，所以可以将每个时刻的海缆形状看成静止状态的悬链线，其长度和形状没有改变。据MAKAI资料介绍，湿设备入水后就会立即加速，那么湿设备受到布缆设备拉力的影响就会变小，导致湿设备的下沉速度比两端海缆的下沉速度快，呈V字型。从安全角度上讲，均匀慢速布放可以更好地控制湿设备下沉的速度，不至于“砸”向海底；另外，均匀慢速布放可以更好地控制布放的余量，而V字型加速布放可能会产生多余的余量。因此，均匀慢速布放的敷设方式更为可取。

URADUCK套管的布放，除了不同类型海缆的交越可能出现在较为平坦的海底地形，大多数情况下海底的坡度还是较大的。因此，悬链线模型在较大坡度情况下的应用就变得很关键。下坡敷设时，悬链线的最低点不会与斜坡接触，而是悬链线的左侧与斜坡相切。

下面以水深为H米，下坡坡度角为θ，悬链线系数a恒定的情况进行计算和讨论。图1为基于悬链线模型的下坡敷设情况的分析图。

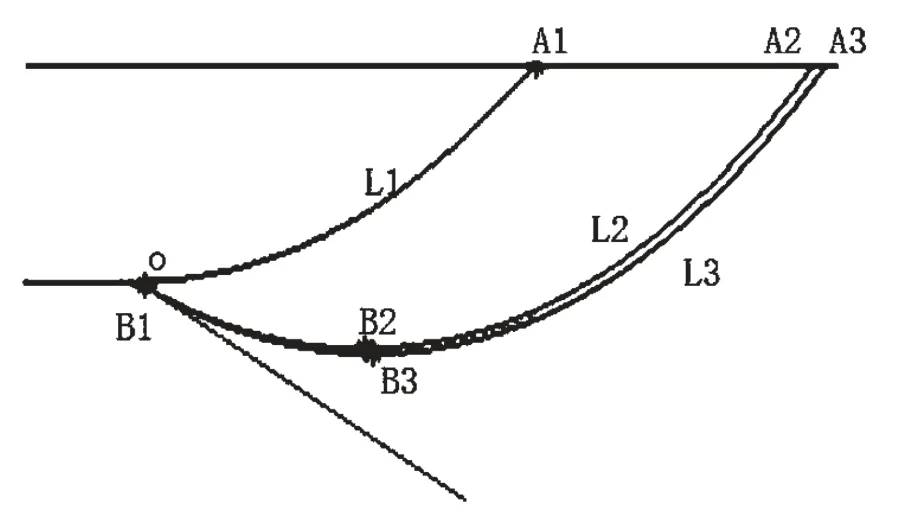
图1　基于悬链线模型的下坡敷设情况分析

状态1：悬链线最低点与平坦的海底相切，O点为原点，A1为船的悬挂点(x1,y1)，且A1的纵坐标等于水深H，悬链线弧长为L1，且有：

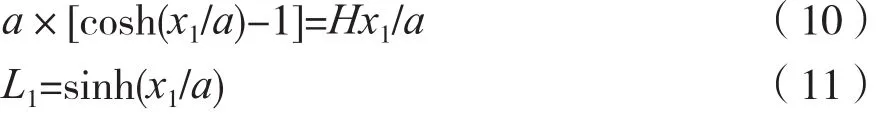
状态2：悬链线的左侧开始与斜坡相切，B2点为悬链线最低点，且为状态2下悬链线原点(0，0)，O点为状态2下悬链线与斜坡相切的位置(-x2,y2)，A2为船的悬挂点（x3，y3），B2A2弧长为L2，OB2弧长为S，有：

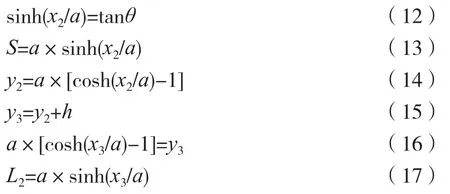
式中θ取正值，因此x2也为正值。

令船只敷设海缆长度为L，船只前进的距离为l，则有如下关系：

状态3：悬链线的左侧与斜坡相切，船只继续敷设海缆，且海缆开始逐渐着底。B3为状态3下悬链线的原点（0，0），A3为船的悬挂点（x4，y4），B1为悬链线与斜坡的切点，且弧长OB2等于弧长B1B2，弧长A3B3为L3，着底的海缆长度OB1为m，有如下方程：

令船只从状态2到状态3过程中敷设的海缆长度为L'，船只前进的距离为l'，则有：

通过以上方程求解可得到如下结论：

第一，从状态1到达状态2，虽然有海缆的布放，但海缆并没有着底，且敷设海缆长度L，船只前进距离l'与水深θ、坡度角θ、悬链线系数a有如下关系：

例如，水深H为2 000 m，敷设过程中的悬链系数a保持为4 000，则可计算出船只从状态1到状态2共敷设海缆3 110.969 3 m，前进距离为2 706.125 2 m。

第二，从状态2开始，已有海缆逐渐着底。从状态2到状态3，船只敷设海缆长度L'、前进距离l'与海水深度H、坡度角θ、悬链线系数a有如下关系：

例如，着底的长度为100 m，则船只敷设海缆长度为162.621 4 m，前进距离为124.304 4 m。

第三，从如上表达式和例证中可以看出，在整个下坡敷设过程中，布缆的速度始终大于船速。据目前国内的施工资料显示，上下坡敷设套管时，布放速度和船速都是恒定且相等的，这并不合理的。例如，下坡时，布缆速度与船速恒定，就会导致悬链线系数的增大，即悬链线就会越平坦，导致着底点的残余拉力上升，最终超过NPTS。为了避免这种不利情况的出现，应该使布缆的速度大于船速。

第四，上坡敷设情况的计算仍然可以依据上面的思路，这里不再累赘。可以预测，基于悬链线模型的上坡敷设，会要求布缆的速度小于船速，而不是相等的关系。

第五，以上敷设海缆长度和船只行驶的距离除以时间，就可以转换到布缆速度和船速。但是，这有一个必要的前提：时间要足够长，即慢速行驶。

3　结 语

本文简要介绍定余量敷设和定张力敷设两种控制方式，并比较了两种敷设控制方式，得出了定张力敷设的控制方式不适用深海敷设的原因。然后，介绍现有深海定余量敷设的直线模型，并就实际深海敷设的情况，提出了慢速布放的悬链线模型。最后，重点分析了下坡敷设的情况，得出了海缆敷设长度L、船只行驶距离l和水深H、坡度角θ、着底缆长m的关系。

海缆着底点的张力是非常重要的参数。张力过小，会导致海缆的打扭；张力过大，可能会超过NPTS，从而降低海缆的性能，减少海缆的使用周期。在敷设模型中，海缆着底点张力直接影响海缆悬链线的平坦程度，而这也决定了海缆与海底地形伏贴的程度。

无论是直线模型还是悬链线模型，都是基于理想的海况，即无海流的影响。事实上，这种理想的海况是不存在的。因此，要想更好地了解海缆实时的悬浮情况，必须借助于实时动态的仿真系统[7]。相信随着现代仿真技术的进步，不久人们将可以更加直观地了解海缆的敷设情况。

[1] 郭胜利.海底光缆铺设与埋设施工程序及方法[M].北京:机械工业出版社,2013:29-35. GUO Sheng-li.Procedures and Methods of Laying and Embedding of the Submarine Fiber Cable[M]. Beijing:China Machine Press,2013:29-35.

[2] 蒋晖.海底光缆深海敷设余量的研究[M].北京:机械工业出版社,2009:25-33. JIANG Hui.Research of Deep-sea Deployment Slack of Submarine Fiber Cable[M].Beijing:China Machine Press,2009:25-33.

[3] 陶新华.用悬链线模型估算海床上海光缆的NPTS[M].北京:机械工业出版社,2013:147-155. TAO Xin-hua.Estimate the NPTS of Fiber Cable on the Seabed with Catenary Model[M].Beijing:China Machine Press,2013:147-155.

[4] 曾达人.海底通信电缆工程技术手册[M].北京:解放军出版社,2000:251-258. ZENG Da-ren.Undersea Communication Cable Engineering Technical Manuals[M].Beijing:PLA Publishing Press,2000:251-258.

[5] 董向华,靳煜.海缆船开始和停止布缆时海缆敷设状态的研究[M].北京:机械工业出版社,2009:34-38. DONG Xiang-hua,JIN Yu.Research of the Deployment Situations of Submarine Fiber Cable at the Start and the Stop[M].Beijing:China Machine Press,2009:34-38.

[6] 谢春童.浅海光缆维修中海光缆受力分析[J].海缆技术,2015,1(33):1-12. XIE Chun-tong.Force Analysis of the Maintenance of Submarine Fiber Cable in the Shallow Sea[J].Submarine Cable Technology,2015,1(33):1-12.

[7] 徐享忠,于永涛,刘永红.系统仿真[M].第2版.北京:国防工业出版社,2012. XU Xiang-zhong,YU Yong-tao,LIU Yong-hong.System Simulation[M].(Second Edition).Beijing:National Defence Industry Publishing,2012.

柯 超（1992—），男，硕士，主要研究方向为海底光缆通信系统、海缆敷设技术；

王瑛剑（1976—），男，硕士，副教授，主要研究方向为海底光缆通信技术；

张鹏杨（1991—），男，硕士，主要研究方向为海底光缆埋设深度。

Technical Research of Deep-sea Fiber Cable Deployment based on the Catenary Model

KE Chao, WANG Ying-jian, ZHANG Peng-yang
（College of Electronic Engineering, Naval University of Engineering, Wuhan Hubei 430033, China）

The quality of sea cable laying directly determines the service life of the optical cable system.The article introduces the differences and compare the applicabilities between the undersea fiber cable fixedslack deployment in the deep sea and fixed-tension deployment in the shallow sea.And the paper briefly introduces the relatively mature liner model of fixed-slack deployment and its applications.According to the analysis of the limitation of the liner model,the deep-sea fiber cable laying model based on the catenary has been proposed.There is a selective analysis in the situation of the deployment on the downhill and the relationship of the length of the undersea fiber cable paid out and the distance of ship's moving,namely the relatiobship of the speed of the cable deployed and the speed of the ship.The research has a guiding significance for the control of deep-sea fiber cable deploment.

deep-sea fiber cable; fixed-slack deployment; the liner model; the catenary model

TN929.11

A

1002-0802(2016)-08-01104-05

10.3969/j.issn.1002-0802.2016.08.028

2016-04-16;

2016-07-18

date:2016-04-16;Revised date:2016-07-18