一类卷积码的随机交织参数盲识别方法*

涂 榫，王伟玮，刘晓龙

（解放军78009部队,四川 成都 610066）

一类卷积码的随机交织参数盲识别方法*

涂 榫，王伟玮，刘晓龙

（解放军78009部队,四川 成都 610066）

针对卷积码随机交织参数的盲识别问题，重点对随机交织关系进行研究，提出了一种针对(2,1,m)卷积码随机交织参数进行盲识别的方法。该方法通过建立矩阵分析模型，在获取卷积码编码参数和交织长度的基础上，利用列删除矩阵的秩准则算法确定子码交织关系，进而利用基构造法和穷举比对法确定随机交织关系，实现了对(2,1,m)系统/非系统卷积码随机交织参数的盲识别。实验仿真表明，在仅获取含误码的卷积码交织后数据序列的情况下，实际数据的编码、交织参数识别分析结果正确。

卷积码；随机交织；盲识别；矩阵分析

0 引 言

数字通信系统中，通信编码都会遇到多径衰落和其他突发噪声的影响，而干扰产生的错误是突发的。在传输前对编码信息进行交织，分离相邻的码元，可使信道的突发错误在时间上得以扩散，从而使译码器可将它们当作随机错误处理，以增强译码的准确率。目前，常用的交织方式有分组交织（矩阵交织、随机交织）和卷积交织，而交织技术已在实际通信中大量使用。交织识别已经成为纠错码识别的关键，因此研究交织技术具有重要的价值。

在实际卫星通信中，信道编码通常使用卷积码和随机交织级联的方式。随机交织是按照某种交织（置换）关系，对交织长度内的码元重新进行排序，实质上也是分离相邻的码元。由于置换关系无规律可循，分离后的相邻码元之间的距离可能毫无规律，因此分析难度较大。目前，常用的卷积码为(2,1,m)非系统码和删余码。

卷积码随机交织的盲识别方法尚不多见。文献[1-2]仅对交织长度、起点和码率进行了盲识别，尚未对交织关系进行分析。文献[3]利用反转误码率最小准则对线性分组码伪随机交织进行识别。该方法将截获序列按可能的编码、交织等方式进行译码后再进行编码、交织，将所得新序列与原截获序列进行比较。由于该方法需遍历所有的可能，运算量较大，效率较低，且仅能对基于m序列的伪随机交织关系进行识别。文献[4]使用的遍历、比对的方法则仅能对标准的(2,1,m)卷积码的随机交织进行识别，且该方法不便于程序实现。

针对以上盲识别方法的局限性，本文提出了一种新的方法，即在识别交织长度的基础上，采用列删除矩阵的秩准则算法确定子码交织关系，再利用基构造法和穷举比对法确定随机交织关系。该算法不仅适用于标准的、非标准的(2,1,m)卷积码随机交织的识别，而且使可能的交织方式个数相比于文献[3-4]大幅降低，减少了遍历次数，提高了盲识别效率。

1 卷积码随机交织识别分析

设随机交织前使用的纠错编码方式为(n,k,m)卷积码，信息序列经卷积编码后生成序列c，c经随机交织后产生传输序列L，交织长度L。

为保证编码和交织结合的最优性能，随机交织和卷积码之间满足如下条件：

（1）交织长度L大于或等于编码约束长度，且一般是卷积码码长n的整数倍。

（2）交织块以卷积序列的一个分组起点为起点。

（3）块内连续性，即一个交织块内的L位，交织前是连续的L位卷积序列。

（4）块间连续性，即块与块之间是按时间顺序排列的，不会出现倒序。

（5）同组同块性，即卷积码的同一码字在同一交织块内。

交织分析需要识别的未知参数包括交织长度L、交织起点i、交织前的卷积码编码参数及交织关系。

1.1 建立矩阵分析模型

将接收序列u按行写入的方式构成一个p×q矩阵，行数p至少为交织长度的2倍（序列u长度应大于p2），列数q取值小于行数p。

1.2 交织长度L的确定

定理1：由卷积码性质可得，序列c所构成的p×q矩阵，当列数q为交织长度L的整数倍（也为码长n的整数倍）时，矩阵的秩小于列数q。

引理1：序列u是序列c经随机交织而产生的，序列u构成的p×q矩阵是由序列p×q构成的p×q矩阵（q为交织长度L的整数倍）经列置换产生的，而初等列变换不影响矩阵的秩。

由引理1知，序列u构成的矩阵的秩小于列数q。此外，由引理1知，对于标准化后左上角单位阵的维数相等、秩小于列数的矩阵，其列数为交织长度L的整数倍，则对不满秩矩阵的列值取最大公约数，即可得到L。

受实际信道误码率的影响，p×q矩阵是由含错交织序列ue构成。因此，矩阵中的元素不一定满足编码序列本身的校验关系，且这种校验关系可能会被完全破坏，从而导致矩阵满秩。

对于(n,k)线性分组码码字按行写入构成的p×n矩阵X(p＞n)，定义其码字空间C⊥的零空间（对偶空间）为C⊥，即C⊥={h|∀c∈C,hcT=0}。于是，有以下定理[5]：

定理2：对于任意的q维二元域行向量h，有∀h∉C⊥，w(hXT)的均值在p/2附近；反之，∀h∈C⊥，w(hXT)小于p×(1-(1-2τ)w(h))/2。其中：w(h)表示信道误码率，w(h)表示向量h的汉明重量。

推论1：定理2对卷积码仍然适用，即对(n,k,m)卷积码码字按行写入构成的p×q矩阵X（p＞q, q≥n×(m+1),q为n整数倍），结论仍成立。

推论2：由引理1和推论1可知，含错编码序列ue按行写入构成的p×q矩阵X（q为交织长度L的整数倍），结论仍成立。

对于矩阵X，利用伽罗华域上的高斯约当消元法，对X进行初等行列变换，化成一个下三角矩阵，则有P·X·Q=A，其中A是一个下三角矩阵，其上半部分近似为一个单位阵，矩阵X的具体变换可参考文献[6]。

记Q(:,i)、A(:,i)分别表示矩阵Q和A的第i列，矩阵P对X仅做行变换，则有w(X·Q(:,i)=w(A(:,i))。

如果A(:,i)的汉明重量为零或者小于一个检测门限阀值Tres，即：

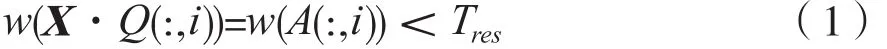
根据推论2，Q(:,i)属于X的零空间，也是方程组X的一个解向量，满足式（1）的所有Q(:,i)构成方程组X的一个基础解系，也构成含错编码序列ue的校验矩阵。设满足式（1）的列数为η，此时矩阵X的秩为q-η，对不满秩矩阵的列值取最大公约数，就可得到交织长度i。

1.3 交织起点i的确定

引理2[4]：序列u按行写入构成的p×q矩阵（p＞2L,q为L整数倍），当交织起点与矩阵每行起点重合时，其标准化矩阵的秩最小。

对于构造的分析矩阵，列数取交织长度L的整数倍，然后对矩阵移位L-1次，当交织块起点正确时，矩阵中相关的列最多，秩最小，根据最小秩确定交织起点。

对于含错序列ue，采用上文中提到的容错处理技术求取构造矩阵的秩。

交织块的块内连续性保证了交织块内不含有两个或两个以上的子交织块，即保证了交织起点具有唯一性。实际通信中，可能存在交织块中含子交织块的情况，子交织块数量即为可能的交织起点个数。这时需对每个可能的交织起点分别确定交织关系。

1.4 卷积码码长n和信息位长k的确定

在确定交织长度L和交织起点i的基础上，令[u]2L、[u]L分别为序列u按行构成的2L×2L维、L×L维分析矩阵，其秩分别为r([u]2L)和r([u]L)。于是，可按式（2）确定n、k。

1.5 交织关系的确定

实际通信中，使用卷积码和随机交织级联的方式时，常用的卷积码为(2,1,m)非系统码和删余码，本文重点对(2,1,m)非系统码进行讨论。假定每一时间单位输入卷积码编码器的信息元均参与子码（各支路）的运算，同时存储在第一个存储器内。这和实际应用的各类(2,1,m)码的编码器相吻合。

设(2,1,m)卷积码的生成多项式G(D)=[g(1,1)(D), g(1,2)(D)]，监督多项式H(D)=[h(1,1)(D),h(1,2)(D)]，生成元g=(11xx……xx)(x表示0或1)，则可采用改进高斯法[7]快速求取监督元。根据文献[8]，g(1,1)(D)=h(1,2)(D)，g(1,2)(D)=h(1,1)(D)，则监督元h=(xx……xx11)(x表示0或1)。

引理3[9]：当不知道卷积码子监督多项式的次数时，为求取系数，可把它们的次数适当假设得大一些，然后约去公因式，得到次数最低的多项式，即为子监督多项式。

根据引理3，设(2,1,m)卷积码的监督元为h，当卷积码构成p×q矩阵(p＞q,q≥2(m+1),q=2a,a为整数)，其监督元信号空间的一组基｛φi｝如下，维数为a-m：

这里，将生成这组基的方法定义为基构造法。

推论3：监督元h=(xx……xx11)的(2,1,m)卷积码，按行写入方式构成p×q矩阵(p＞q,q＞2(m+1)) q=2a,a为整数)，删除列值区间在2(m+1)+1～2a的任意两列，则删除最后两列形成的列删除矩阵的秩是所有删除组合中秩值最小的。

证明：删除矩阵最后两列后，监督元信号空间的一组基{φi}的个数为a-m-1，φi(i∈[0～a-m-2])为φi（i ∈［0~a-m -2］）删除最后两位0得到。监督元的0意味着该位不参与校验，不会影响约束关系；而φa-m-1的最后两位是1，删除意味着φa-m-1表示的约束关系被破坏。删除后，矩阵的秩为a+m-1，其余删除组合分以下两种情况进行讨论：

①删除同一子码的两列

设删除的两列列值为2(m+1)+2ε-1、2(m+1)+2ε(ε∈[1～a-m-2])，则φε对应位置的值为11，φi（i＜ε）对应位置的值为00。若φi（i＞ε）对应位置的值全为00或11时（若是11，可通过二元域上线性变换变为00），删除后矩阵的秩为a+m-1，原理同上；若φi（i＞ε）对应位置的值不全为00或11，删除两列时，有且仅有2个约束关系会被破坏，故删除后矩阵的秩为a+m。

②删除不同子码的两列

设删除的两列分属第i、j个子码(i,j∈[m+2～a],i≠j)，则除φi、φj以外，其余约束关系对应位置的元素可通过初等变换变为0，φi、φj的约束关系被破坏，删除后矩阵的秩为a+m。

1.5.1 子码交织关系的确定

交织长度L的子码交织关系确定方法如下：

①序列u按行构成p×2L(p＞2L)维矩阵，从L+1列至2L列遍历删除两列。当列删除矩阵的秩最小时，删除的两列属交织前的同一子码，即确定了交织长度L中第L/2个子码的交织关系（L中共含L/2个子码），并令k=1。如果秩最小值不唯一，需遍历每种可能分别进行讨论。

②删除已确定的两列，对列删除后的p×(2L-2k)维矩阵按步骤1求最小秩，确定L中第L/2-k个子码的交织关系，令k=k+1，并记列删除矩阵为Xi（i表示矩阵列数值）。

③若列删除矩阵的列数≥L+4，重复步骤2；若列数为L+2，结束。

1.5.2 卷积码编码存储m的确定

①序列u按行构成p×L(p＞L)维矩阵，令k=1。

②按子码交织关系删除第L/2-k+1个子码的两列，记列删除矩阵为Xi（i表示矩阵列数值）。若删除后的p×(L-2k)维矩阵不满秩，令k=k+1，重复步骤2；若满秩，记满秩时矩阵的列数为q，则m=q/2。

1.5.3 随机交织关系的确定

引理4：交织后卷积码的监督元，与交织前卷积码的监督元经交织变换后一致。

（1）根据容错处理技术，求取矩阵X2(m+1)的监督元μ。根据引理4，该监督元是由交织前序列c的监督元v经过交织置换后形成的。结合μ和子码交织关系，产生所有可能的v和部分随机交织关系。

具体方法如下：

若μ中属同一子码的两位相等（都为0或1），则v中对应子码的两位即可确定；若μ中属同一子码的两位不等，则v中对应子码的两位为01或10，即产生两种可能；若μ中共计k个子码不等，则v共有2k种可能，分别记录每种可能和每种可能对应的部分随机交织关系。

（2）穷举所有可能的v，对交织前、后的监督元分别在二元域上张成监督元空间。如果v估计正确，则监督元具有一一对应的关系，反之会出现不匹配情况。

具体步骤如下：

①依次穷举所有可能的v，令k=1。

②对X2(m+1)+2k按照容错处理技术求取交织后监督元空间的一组基，维数为k+1；在二元域上通过线性变换张成的监督元空间个数为2k+1-1，记为α。通过基构造法，由v张成交织前监督元空间的个数也为2k+1-1，记为β。

③遍历β，结合部分随机交织关系，在α内寻找匹配的监督元。根据β中子码内元素不等的位置，对匹配的两个监督元，检验已确定的交织关系，并确定新的交织关系。

如果监督元不能一一匹配或不满足部分随机交织关系，返回步骤①；否则，令k=k+1，返回步骤②，直至随机交织关系全部确定。

至此，(2,1,m)卷积码随机交织的各个参数已全部确定。如果实际中误码率过高，在容错处理技术的基础上，可采用迭代加权累计的方法[10]求取交织长度、起点及监督元。

2 误码率及参数对正确识别率的影响

交织关系的盲识别正确率与卷积码编码参数、交织长度和信道误码率有关。误码率越高，交织长度越长，卷积码约束长度越长，则识别率越低。(2,1,6)卷积码在交织长度为18的情况下，识别率和误码率的关系如图1所示。针对(2,1,6)码，本文方法在误码率小于0.001时，识别准确率可达70%以上。(2,1,6)卷积码在误码率为0.5×10-3情况下，识别率和交织长度的关系如图2所示。

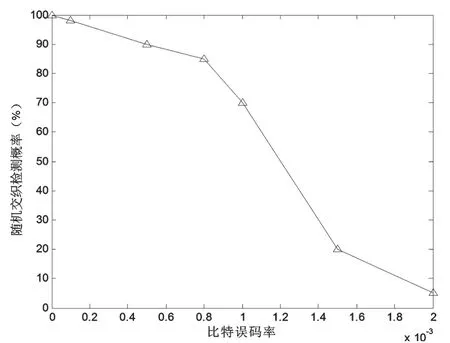
图1 不同比特误码率下的随机交织检测概率

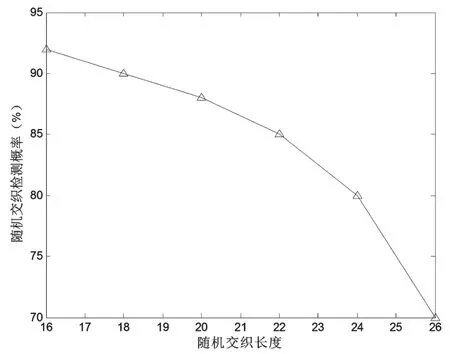
图2 不同交织长度下的随机交织检测概率

3 仿真实验

设信道转移概率为0.001，以某1/2码率的随机交织卷积码接收序列为例，取一段输出数据序列作为识别序列进行分析。

确定矩阵行数p=200，取定列值范围(2,190)，按列数变化将识别序列以按行写入方式构成矩阵，依次计算矩阵的秩，记下秩不等于列数的列值，依次为(36,54,72…)，列值和矩阵的秩如表1所示。交织长度为记录列值的最大公约数，故L=18。

表1 列值与矩阵的秩

分析起点时，取矩阵列值q=36，依次对进行移位并求秩，移位数和矩阵的秩如表2所示。当序列移9位时，矩阵的秩最小，即为随机交织的起点。

表2 移位数与矩阵的秩

根据式（2），卷积码码率为1/2，即

取矩阵列值q=36，遍历删除X36列值区间为19～36的任意两列。当删除第21、30列时，列删除矩阵X34的秩为23，删除其余两列时，秩均为24；继续对列删除矩阵X34进行两列删除的处理，当删除第8、12列（相当于原X36矩阵的第9、14列）时，列删除矩阵X32的秩最小；依次进行计算，同时记录各个Xi矩阵，可确定每个子码的交织关系，最终确认的子码交织关系为：

其中，13/14表示在交织长度内，交织后的第1位来自于交织前的第13位或第14位，即来自于交织前的第7个子码中的任一位。

分析卷积码编码存储m时，取矩阵列值q=18，依次删除X18子码交织关系中数字最大的两列并求秩。根据首次满秩时的矩阵列数值，可确定m=6，编码约束度na=2(m+1)=14。同时，记录每个列删除矩阵Xi，列删除矩阵的列值和矩阵的秩如表3所示。

表3 列删除矩阵的列值与矩阵的秩

求取X14的监督元μ=[11011110111100]，根据子码交织关系，发现共有两个码字内的比特不等，故交织前监督元v共有4种可能：

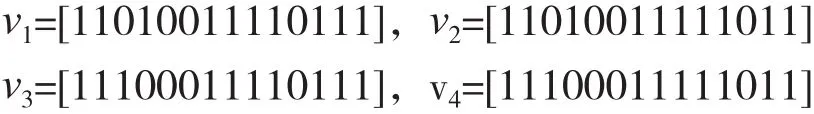
依次检验这4种可能。这里，以对v1的检验为例进行说明，其余3种的检验类似。

①v1确定子码交织关系中的(3/4,11/12,3/4,11/12)为(3,12,4,11)；

②求取X16的2个监督元，张成的监督元空间为h1-h3（共3个）；通过基构造法，由v1张成的交织前监督元空间为H1-H3；通过已确定的部分随机交织关系，可得到如下所示的一一对应关系：

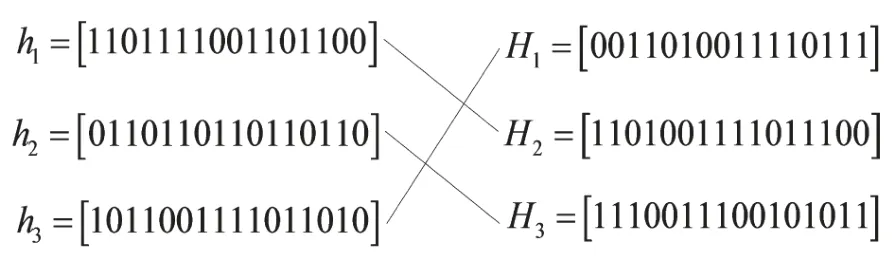
从一一对应关系中又可确定部分新的随机交织关系为：(13/14,5/6,13/14,5/6)→(14,6,13,5)。

③求取X18的3个监督元，张成的交织前后监督元空间共7个，一一对应关系如下所示：

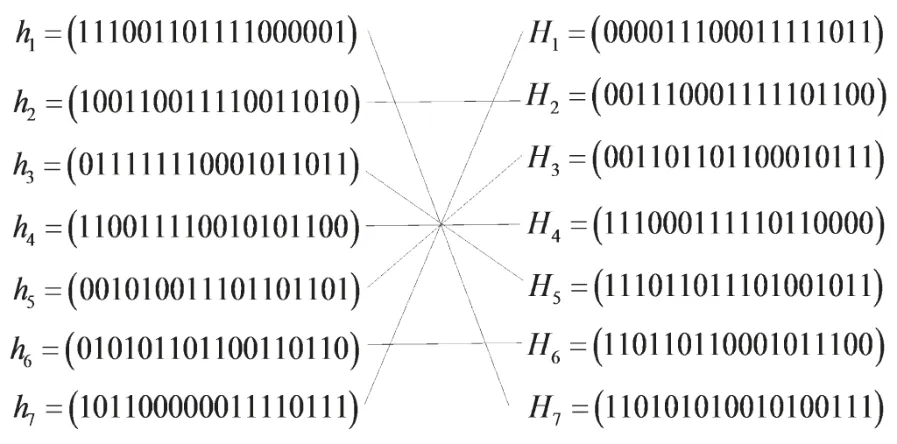
于是，确定部分新的随机交织关系为：

(7/8,15/16,7/8,15/16)→(7,15,8,16)。

类似地，求取X20的交织前后监督元空间，可确定部分新的随机交织关系为：(17/18,9/10,9/10,17/ 18)→(18,9,10,17)；求取X22的交织前后监督元空间共31个，根据已确定随机交织关系进行验证时，无法实现一一匹配，故判断v1不正确。

最终，求取的交织关系和原卷积码生成多项式如表4所示。

从表4可看出，两种有解情况的原码子生成多项式刚好互换，交织置换关系中1个码元内2个比特的位置也正好互换。可见，若先按置换关系解交织，再以生成多项式进行译码，则两种情况得到的原信息序列是完全一样的。

表4 交织关系和生成多项式

4 结 语

卷积码随机交织盲识别技术是一个新兴的研究方向，由于其置换关系具有随机性，故造成对其进行盲识别分析的技术难度较大。笔者提出利用基构造法和穷举比对法确定随机交织关系的方法，完整解决了(2,1,m)类卷积码随机交织参数的盲识别问题。该方法计算复杂度较低，数据利用率较高，容错性能较好。仿真实验表明，在10-3误码率情况下，本文算法能实现对随机交织长度为18的(2,1,6)非系统卷积码交织参数的有效估计，在卫星通信领域具有一定的实用价值。

[1] Sicot G,Houcke S,Barbier J.Blind Detection of Iinterleaver Parameters[J].Signal Processing,2009,89(04):450-462.

[2] Burel G,Gautier R.Blind Estimation of Encoder and Interleaver Characteristics in a Non Cooperative Context[M].Nrnaonal Onfrn on Ommnaon,2003.

[3] 廖斌,张玉,杨晓静.基于线性分组码的伪随机交织识别[J].探测与控制学报,2013,35(04):53-57. LIAO Bin,ZHANG Yu,Yang Xiao-jing.Blind Recognition of the Pseudo-random Interleaver Based on Linear Block Code[J].Journal of Detection & Control,2013,35(04):53-57.

[4] 张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010. ZHANG Yong-guang.LOU Cai-yi.Channel Coding and Identification[M].Beijing:Electronic Industry Press,2010.

[5] Valembois A. Detection and Recognition of A Binary Linear Code[J].Discrete Applied Mathemati cs,2001,111(1-2):199-218.

[6] 刘宗辉.交织和分组码参数盲估计与识别技术[D].成都:电子科技大学,2011. LIU Zong-hui.Blind Estimation and Recognition Technology of Interleaving and Block Code Parameters[D].Chengdu:University of Electronic Science and Technol,2011.

[7] 底强,苏彦兵,刘杉坚.基于改进高斯法的卷积码盲识别方法[J].通信技术,2012,45(10):68-70. DI Qiang,SU Yan-bing,LIU Shan-jian.Blind Recognition of Convolution Code based on Improved Gauss Algorithm[J].Communications Technology,2012, 45(10):68-70.

[8] 刘健.信道编码的盲识别技术研究[D].西安:西安电子科技大学,2010. LIU Jian.Research on Blind Recognition Technology for Channel Coding[D].Xi'an:Xidian University,2011.

[9] 刘玉君.求解非系统卷积码监督矩阵算法的研究[J].信息工程大学学报,2008,9(04):427-430. LIU Yu-jun.Studies on the Algorithms for Acquiring the Check Matrix of Nonsystematic Convolution Codes[J].Journal of Information Engineering University,2008,9(04):427-430.

[10] 彭淼.信道编码参数盲估计技术研究[D].成都:四川大学,2013. PENG Miao.Research on Blind Estimation Parameters of Channel Coding[D].Chengdu:Sichuan University,2013.

涂 榫（1982—），男，硕士，助理工程师，主要研究方向为卫星通信信号处理和信道编码识别；

王伟玮（1982—），男，硕士，助理工程师，主要研究方向为卫星通信信号处理和信道编码识别；

刘晓龙（1983—），男，硕士研究生，主要研究方向为卫星通信信号处理和信道编码识别。

Blind Recognition Algorithm based on Random Interwoven Parameter of A Convolution Code

TU Sun, WANG Wei-wei, LIU Xiao-Long
（Unit 78009 of PLA,Chengdu Sichuan 610066,China）

Aiming at the problem of blindly recognize convolution code random interwoven, mainly study on the relationships of random interwoven is mainly studied, and a method of random interwoven parameter with(2,1,m)convolution code is proposed. The method first build the matrix analysis model, then on the basis of obtaining the parameter of convolution code and the length of interwoven, use the way of the minimum rank of delete column matrix to confirm the sub-code interwoven relationships, and use base construction and exhaustive comparison to ensure random interwoven relationships, finally recognize (2,1,m)systematic/ nonsystematic convolution code random interwoven parameter blindly. Experimental simulation results show that, in the case of only known after-mixed convolution code data sequences which contain errors, the actual data’s encoding, recognition analysis results of interwoven parameter are correct.

convolution code;random interwoven;blind recognition;matrix analysis

TN911

A

1002-0802(2016)-07-0836-06

10.3969/j.issn.1002-0802.2016.07.008

2016-03-08;

2016-06-09 Received date:2016-03-08;Revised date:2016-06-09