基于随机译码算法的全并行架构*

云飞龙，肖 银，张 迅，朱宏鹏，吕 晶

（1.中国人民解放军理工大学， 江苏 南京 210001；2.中国人民解放军75707部队，广西 南宁 530000）

基于随机译码算法的全并行架构*

云飞龙1，肖 银2，张 迅2，朱宏鹏1，吕 晶1

（1.中国人民解放军理工大学， 江苏 南京 210001；2.中国人民解放军75707部队，广西 南宁 530000）

随机译码算法因实现电路简单，被广泛应用于LDPC码全并行译码架构。介绍几种随机译码架构，简化基于MTFM（Majority-based Tracking Forecast Memories）的随机译码架构，将MTFM架构中的加法器改为简单的与门电路，进一步降低了资源消耗。同时，针对CCSDS标准（8176，7154）LDPC码进行性能仿真分析，表明基于MTFM的随机译码算法与最小和译码算法相比，只有0.2 dB的损失。此外，对改进前后的MTFM架构进行资源消耗比较，结果显示每个变量节点改进后比改进前资源相比少了一个slice，且当码长很长时，改进方案的资源消耗大幅降低。

随机译码；全并行；简化MTFM；LDPC

0 引 言

LDPC（Low-Density Parity-Check Code）是20世纪60年代初期由Gallager博士提出的[1]。由于优越的译码性能、可并行译码以及相对其他码字较低的译码复杂度等特点，LDPC已经成为大部分通信系统的首选编码方案，如CCSDS、DVB-S2、GPS和WiMAX等。

LDPC码译码架构上共有3种，全串行、部分并行以及全并行译码架构。其中，全并行译码架构发挥了LDPC码全并行译码的潜力。然而，由于全并行带来的资源消耗巨大，尤其码长较长时，其资源消耗会急剧增加，因此大部分译码架构都会避开全并行架构。鉴于此，本文引进随机译码算法，同时介绍了几种译码架构[2-4]。与传统的基于最小和译码算法[5]的架构相比，本文的随机译码架构能大幅度降低资源。其中，针对基于MTFM的全并行架构进行简化，将MTFM架构中的n输入加法器简化为n输入与门电路。结果显示，一个变量节点减少了一个slice资源。而当LDPC码长为几千甚至几万时，简化后的架构资源消耗将得到大幅度降低。

1 随机计算概念及其译码算法

1.1 随机计算概念

在随机计算中，概率值用一串比特流表示，从而一些复杂的概率运算如采用随机计算实现，只需简单的门电路就可完成。同时，由于处理的单位是比特，因此大大降低了网络布局布线复杂度，有效提高了硬件时钟频率[6]。

概率的比特流表示不是唯一的。例如，对于概率0.875=7/8，其比特流表示有以下几种，如图1所示。

比特流表示的意义是‘1’在比特流中出现的概率，而‘1’的位置不影响比特流的表示值。图1中，比特流表示8个比特中有7个比特是1，即‘1’的概率是0.875。

随机比特流一般用一个比较器产生，如图2所示。用一个随机数S与概率值P做比较，如果P＞S，则输出比特‘1’，否则输出‘0’。若随机数的序列够长，则输出的比特流中‘1’出现的概率就会近似接近概率P。

图2 比特流产生

随机计算的除法通过JK触发器来实现。假设输入的比特流概率为p1、p2，输出的概率为p3，则JK触发器如图3所示。

图3 JK触发器

图3所表示的除法公式为：

JK触发器的真值表则如表1所示。

表1 JK触发器真值表

1.2 随机译码算法

LDPC码译码算法基于因子图，如图4所示。

图4 因子图

图4中，因子图分为变量节点vi以及校验节点ci，因此又被称为二分图。变量节点与校验节点之间的连线称为边。译码过程就是变量节点与校验节点之间信息传递的过程。随机译码算法的特点是校验节点与变量节点之间来回传递的信息是比特，因此大大降低了译码复杂度。

随机译码算法主要包括译码信息的初始化、校验节点运算、变量节点运算以及译码判决输出[6]。具体过程如下：

（1）初始化：随机译码算法的初始化，也就是产生所需要的随机比特流，并将它传递给对应的变量节点。将译码概率值与随机数比较，可得对应的随机比特流，如图2所示。在硬件设计中，通常随机数用一个线性反馈移位寄存器产生，如图5所示。

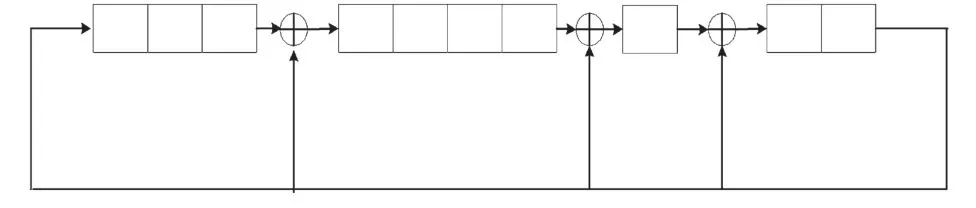
图5 10比特的线性反馈移位寄存器

图5给出了一个10比特的线性反馈移位寄存器，可产生210-1=1023个周期数。将接收到的译码概率值进行量化，并与寄存器中的值比较，每个时钟周期输出一个比特，最后可产生长度为1023的数据比特流。实验表明，所有变量节点可采用同一个线性反馈移位寄存器，且初始化值的不同不影响最后的译码性能[7]。

（2）校验节点运算：假设校验节点的度dc为3，则校验节点的运算电路如图6所示。图6中，a1、a2、a3为校验节点的输入比特信息，由对应的变量节点传递过来；b1、b2、b3为校验节点的输出比特信息，输出给对应的变量节点。

图6 dc=3校验节点电路

（3）变量节点运算：假设变量节点的度dv为2，则变量节点电路图如图7所示。

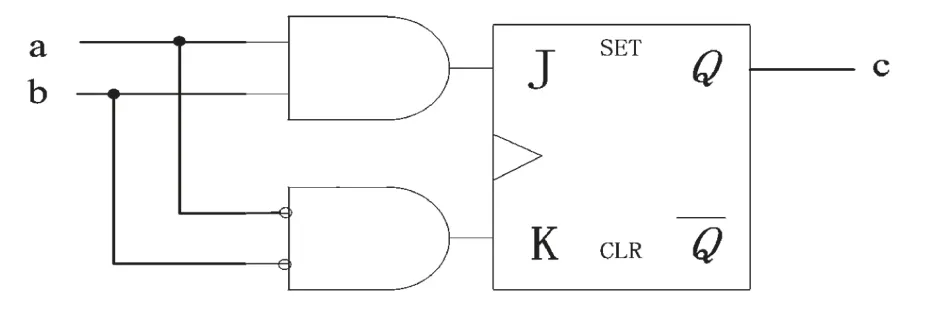
图7 dv=2变量节点电路

图7中，a、b为变量节点的输入比特信息，由对应的校验节点传递过来（在初始化过程中，由初始化模块传递过来），c为变量节点的输出比特信息，输出给对应的校验节点。于是，从表1可得到基于变量节点a、b、c的真值表，如表2所示。

表2 变量节点真值表

（4）译码判决输出：在随机译码中，每个变量节点对应一个有符号位的加/减计数器，每个时钟周期计数器接收到变量节点传递过来的比特信息，初始值一般设为0。如果接收到的变量节点值为‘1’，则计数器加1；如果接收到的为‘0’，则计数器减1。最后，判断计数器的值，若大于0，则输出译码信息为1，否则为0。

2 译码架构的改进

由表2可知，对变量节点的运算，当输入节点值a、b不同时，输出值c保持不变，等于上一时钟周期的值，称为锁存状态。只有当输入值a、b都相等时，输出值c才会等于输入值a、b，称为正常状态。JK触发器的这种特性对译码性能有很大影响。如果出现了误码，即输入节点值不等，则JK触发器就会处于保持状态。而LDPC码中存在环，环会使得这种状态被保持，尤其当高信噪比时，此时概率要么趋近于1，要么趋近于0，从而使得产生的比特流为全1或全0。长时间处于这种状态，导致比特间的信息交换缓慢，最后导致译码性能很差。因此，早期的随机译码算法主要应用于无环的LDPC短码，而LDPC长码对应的环路较多，严重影响随机译码算法的性能[8]。

针对这一问题，Tehrani引入边存储器（Edge Memories，EM）和内部存储器（Internal Memories，IM），打乱比特流间的关系，有效改善了译码性能[2]。

随后，Tehrani又提出了资源更少的预测追踪存储器架构TFM（Tracking Forecast Memories）[3]，用来代替EM。由于TFM与EM一样，都是以二分图中的边为基础，资源消耗仍旧较多。于是人们又提出了一种基于大数逻辑的预测追踪存储器的架构（Majority-based Tracking Forecast Memories，MTFM）[4]。它以变量节点为基础，变量节点的架构如图8所示。

图8 基于MTFM的变量节点结构

图8中，度为4的变量节点分成2级处理，第一级由2个度为2的节点构成。这2个子节点处理完后，将信息传递给第二级度为2的子节点，度为2的节点可由IM架构实现。2级处理完后输出比特si(t)和ri(t)，其中si(t)=0表示第i条边处于锁存状态，si(t)=1表示第i条边处于正常状态，而ri(t)为第i条边子节点输出的比特信息。4个si(t)比特和4个ri(t)比特送入MTFM进行处理，会发现一个变量节点处理单元中，只有一个MTFM，而不像EM和TFM架构，变量节点的每条边都对应一个。因此，MTFM比较节省资源。MTFM具体架构如图9所示。

图9 MTFM架构

图9中，4个si(t)比特和4个ri(t)相加得X(t)值，取其量化后的最高位作为TFM的更新数据，而4个si(t)经过与门操作得到的值作为TFM更新使能信号。

对CCSDS标准的（8176，7154）码字，其每个变量节点的度dv=4。通过观察分析图9发现，若将变量节点的度4量化，则量化后为”100”，即X(t)最高位为1的唯一条件是图9中加法器的4个输入数据都为1。又因只有当4个si(t)都为1时，更新数据值才有效，而此时4输入加法器的4个输入数据都为1的唯一条件是4个ri(t)都为1。因此可将图9中的dv个与门和dv输入加法器直接改为一个dv输入的与门，见图10，dv输入的与门输出为1的唯一条件是dv个ri(t)都为1，而简化后的性能不变。

图10 本文改进的MTFM架构

3 性能分析与资源比较

图11给出了传统的归一化最小和译码算法（NMSA）、分层归一化最小和译码算法（LNMSA）和基于MTFM的随机译码算法的性能比较，仿真条件为AWGN信道和BPSK调制。其中，NMSA和LNMSA算法采用10次迭代，译码6比特量化，同时归一化因子设为0.812 5，而MTFM采用改进后的图10架构进行500次迭代，输入的概率信息8比特量化，β为1/16，λ为5.22，β与λ可参见文献[6]。从图11可看出，MTFM与LNMSA算法相比，性能只有约0.2 dB的损失，而与NMSA算法相比，性能损失更少，不到0.1 dB。对于全并行译码架构，NMSA算法和MTFM可实现；就复杂度来说，MTFM的复杂度远远小于NMSA算法的复杂度。

图11 算法性能比较

图10中，当X(t)=4时，最高位为1，即更新数据为1；当X(t)=0、1、2、3时，最高位为0，即更新数据为0。事实上，可能认为X(t)的取值长度不一样，更新数据为1或0的概率也不一样，从而影响最后的译码性能。为此对其进行性能仿真：第一种，当X(t)=4时，更新数据为1，当X(t)=0、1、2、3时，更新数据为0；第二种，当X(t)=3、4时，更新数据为1，当X(t)=0、1、2时，更新数据为0；第三种，当X(t)=2、3、4时，更新数据为1，当X(t)=0、1时，更新数据为0；第四种，当X(t)=1、2、3、4时，更新数据为1，当X(t)=0时，更新数据为0。图12给出了对应的性能仿真图，仿真条件在AWGN信道以及BPSK调制下，400次迭代，概率信息8比特量化，β为1/16，λ为5.22。从图12可看出，4条性能曲线几乎重合，因此针对CCSDS（8176，7154）的码字而言，这4种情况对最后的译码性能影响不大。

下面进行进一步分析。因为所有si(t)都为1时，即输入的dv个节点都处于正常状态，X(t)值才有用。而此时所有输入节点值都相等的概率很大，且随着迭代次数的增加越来越大。因此，X(t)为最大值或者最小值的概率也越来越大。于是，在最大值与最小值之间的数对最后的译码性能影响不是很大。

事实上，变量节点度码字只是一种特例，恰好满足图10的架构。而由上述分析可知，最大值与最小值间的数对译码性能影响不大，即度为其他值也可采用该架构。然而，如果度dv不同，对译码器设计来说，将会变得比较复杂，需不同的MTFM架构。因此，本文以变量节点度都为4的码字矩阵为例。在文献[4]中，作者同时指出，dv太小，会严重影响MTFM架构的性能。因此，MTFM的架构适用于度dv≥4的码字矩阵。

图12 不同X(t)取值长度的性能比较

通过上述分析，可以得出结论：当校验矩阵的变量节点度dv≥4时，适用于MTFM架构，同样也适用于本文改进后的MTFM架构。

表3给出了本文对MTFM架构改进后（图10中四输入与门）和改进前（图9中四输入加法器，4个二输入与门）之间的资源消耗比较。

表3 改进前后的资源消耗比较

从表3可看出，改进后比改进前资源减少，而每一个变量节点都对应一个MTFM架构。因此，当变量节点较大时，改进后比改进前的资源将大大降低。

4 结 语

本文针对全并行译码架构资源消耗大的问题，介绍了一种随机译码算法。算法实现只需简单的逻辑运算，可大大降低资源消耗，且因处理单位是比特，能有效提高硬件时钟频率。同时，针对算法中变量节点的锁存问题，引进几种改进的译码架构，并基于MTFM的译码架构对其进行简化，提出了一种资源消耗更低的译码架构。结果显示，改进前后性能不变，而每个变量节点的资源消耗减少了一个slice，且LDPC码长较大时，资源消耗将大幅降低。

[1] Gallager R G.Low-density Parity-check Codes[J]. IRE Trans. Inform. Theory,1962,8(01):21-28.

[2] Tehrani S S,Mannor S,Gross W J.Fully Parallel Stochastic LDPC Decoders[J].Signal Processi ng,2008,56(11):5692-5703.

[3] Tehrani S S,Naderi A,Kamendje G A,et al.Tracking Forecast Memories for Stochastic Decoding[J].Journal of Signal Processing Systems,2011,63(01):117-127.

[4] Tehrani S S,Naderi A,Kamendje G A,et al.Majoritybased Tracking Forecast Memories for Stochastic LDPC Decoding[J].IEEE Transactions on Signal Processing,2010,58(09):4883-4896.

[5] 姜明.低密度奇偶校验码译码算法及其应用研究[D].南京:东南大学,2006. JIANG Ming.Decoding Algorithm and Applied Research of Low-Density Parity-Check Code[D].Nanjing:Southeast University,2006.

[6] 朱行信.LDPC码的随机译码研究[D]西安:西安电子科技大学,2013. ZHU Xing-xin.The Research on Stochastic Decoding Algorithm based on LDPC[D].Xian:Xidian University,2013.

[7] Sarkis G,Gross W J.Reduced-latency Stochastic Decoding of LDPC Codes over GF(q)[C].Proc.2010 European Wireless Conf,2010:994-998.

[8] 任祥维,文红,张颂.LDPC码的全并行概率译码[J].通信技术,2011,44(08):42-44. REN Xiang-wei,WEN Hong,ZHANG Song. The All-parallel Probability Decoding Architecture based on LDPC[J].Communication Technology,2011,44(08):42-44.

云飞龙（1990—），男，硕士，主要研究方向为信道编码；

肖 银（1986—），男，学士，工程师，主要研究方向为通信技术；

张 迅（1987—），男，学士，工程师，主要研究方向为通信技术；

朱宏鹏（1982—），男，博士，讲师，主要研究方向为信道编码；

吕 晶（1965—），男，博士，教授，主要研究方向为卫星通信。

Full-Parallel Architecture based on Stochastic Decoding Algorithm

YUN Fei-long1, XIAO Yin2, ZHANG Xun2, ZHU Hong-peng1, LV Jing1
(1.PLA University of Science and Technology,Nanjing Jiangsu 210001,China; 2.Unit 75707 of PLA,Nanning Guangxi 530000, China）

LDPC is applied in full-parallel architecture for its simple implementation of stochastic decoding algorithm.This paper introduces several stochastic decoding architectures and simplifies stochastic decoding architecture based on MTFM(Majority-based Tracking Forecast Memories) which is proposed by the former .In the improved architecture,the adding circuit is replaced by the AND circuit,which reduces the resources effectively.Meanwhile, aiming at the simulation analysis based on the (8176,7154)LDPC in the CCSDS standard, the result suggests that the performance is 0.2 dB close to the Min-Sum algorithm. Besides, the resources of the architecture between the old and the new are compared,and the result suggests that the proposed architecture saves one slice than before.When the length of the LDPC code is long , the resources of the proposed architecture could be decreased significantly.

stochastic decoding algorithm;full-parallel;fimplifying MTFM;LDPC

National Natural Science Foundation of China(No.61401507)

�TN911.22

A

1002-0802(2016)-07-0821-05

10.3969/j.issn.1002-0802.2016.07.005

2016-03-13;

2016-06-09 Received date:2016-03-13;Revised date:2016-06-09

国家自然科学基金(No.61401507)