以“教学生思考"为目标的数学教学案例研究

夏小强

1问题的提出

南京师范大学的涂荣豹先生认为，数学教学的目标有三个：一是使学生爱学；二是会学；三是发展学生的认识力。发展学生的认识力，指的就是数学教学要教学生学会思考。

教师在教学过程中，对数学知识的呈现方式存在差异，这种差异对学生获得数学知识也许影响不大，但对学生数学思维活动的影响，却可能有很大的差别。

2教学内容说明

向量是刻画现实世界的重要数学模型，力、速度、位移等都是向量的实际背景，可以用向量加以刻画和描述。用什么样的数学模型来刻画位移、速度、力这样的量？这个数学模型有什么性质与应用？这就是《平面向量》的中心问题，也是本章的知识学习的固着点。

向量的数量积是在向量的线性运算基础上学习的一种新的运算，向量的线性运算是封闭性运算，而向量的数量积运算是非封闭性运算，运算的对象是二元的，而运算的结果又是一元的，这种运算的非封闭性对学生的认知造成了很大的失衡。

3教学案例分析

笔者近期听了两堂关于“平面向量的数量积”的课，两位老师的教学过程都分为五个环节：问题情境——抽象模型——辨析模型（内涵、外延）——模型性质（运算律）——数学应用，两位老师都是以“问题”的形式来推动教学过程。

本文结合其中的环节一和环节四，来探究在教学中如何实现教学生“学会思考”。

3.1环节一问题情境

甲教师：

师：（问题1）向量的运算有向量的加法、减法、数乘，叫做向量的线性运算，那么向量与向量能否“相乘”呢？

生：能。

师：向量与向量“相乘”这种运算怎么定义呢？

生：应该不是线性运算。

师：为什么？

生：老师，向量的加法、减法、数乘，叫做向量的线性运算，向量与向量“相乘”没有和它们放在一起学，那肯定和它们不一样了。

师：怎么个不一样法？

生：……

师：我们是怎么得到向量的线性运算的，它的结果是什么？

生：是通过将实际生活中，物理中的矢量的合成与分解，速度在某时问段的位移抽象出来的，得到的结果还是向量。

师：你想一想，向量与向量“相乘”的结果是什么呢？

生：应该不是向量了。

师：结果不是向量，只能是什么？

生：数……数量……（不是很肯定）

师（点头）：是数量，我们在实际生活中有这样的物理背景吗？

生：做功，力做功的结果就是标量，是一个数。

师：好，我们来分析这个物理背景。看看从求功的运算中可以抽象出什么样的向量运算？

乙教师：

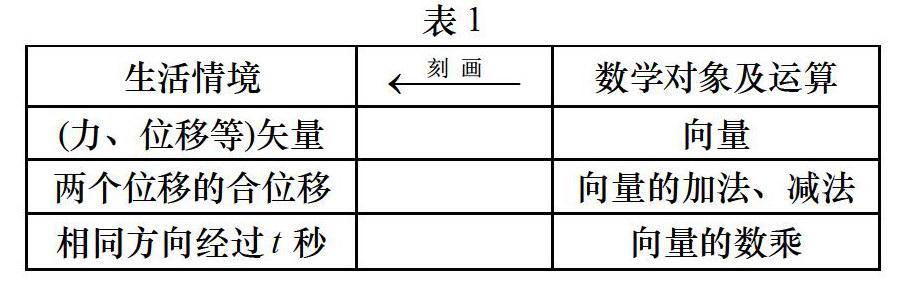
师：前面我们已经学过的向量、向量的加减法、实数与向量的数乘，向量的加法、减法、向量的数乘我们称之为向量的线性运算。它们都是对实际问题的刻画。（附表1）

师：（问题1）向量的线性运算可以刻画出所有的矢量运算吗？

生：（思考了一会）不能，不能形容矢量的做功运算。

师：为什么？

生：矢量的做功得到的结果是一个标量，也就是数，而你列举的三种运算得到的结果都是向量。

师：那怎么办？

生：应该引入一种新的运算，用这种运算来刻画力的做功。

师：你准备如何定义这种运算？

生：现在还没想好，我想我们应该先分析矢量做功这个物理背景，找出这个物理背景中和数学有关的元素。

师：研究数学元素的目的是什么？

生：建立数学的量的关系，就像从力的合成与分解中，得出向量的加法、减法一样。

师：对，建立物理背景中数学的量的关系就是建立数学模型，下面，请大学先分析做功这个物理背景。

教学意图

甲教师：从数学知识内部发展的需要引入概念，前面学习了向量的线性运算，接下来就应该学习向量的非线性运算，并根据线性运算的结果，引导学生得出新运算的结果是数，侧重数学知识的联系和对比。

乙教师：从实际问题中抽象出向量的概念及运算（数学模型），然后用数学的方法研究数学模型，最后再运用数学模型去解决实际问题。突出了知识的来龙去脉，有助于学生对数学完整的认识。

案例分析

情境的引入要能体现学习新知识的必要性，学习新知识的必要性一般有两种情况：一是从数学概念体系的发展过程中引入新概念，也就是从数学的内部出发，在原有知识的基础上，通过归纳、比较、分析等思维活动，寻找新知识与原有知识的区别与联系，建立新的知识，甲教师正是采用这一方式引入的；二是从解决实际问题的需要出发引入新概念，原有的知识不能解决新的问题，需要引入新的知识来刻画，乙教师是采用这种方式引入的。

甲教师的引入虽然体现了新知识与原有知识的联系，但是学生不能认识到学习向量的数量积的必要性，只是因为前面学过了向量的线性运算，所以今天就要学非线性运算，但是学习这个知识有什么用？非线性运算是怎么来的？这些都是通过老师以设问的方式提出来的，虽然学生也能在老师的引导下去研究，但这是一种停留在数学知识本身的学习，这种学习相对被动，学生被老师牵着走，学生的思维难以得到激发。

乙教师的问题情境能够让学生认识到学习向量数量积的必要性，教师的提问不是直接指向数学知识本身，而是通过一系列的元认知提示语，引导学生像数学家一样思考问题，再现知识的“创造”过程，这个“创造”的过程就是研究数学的一般方法。不仅仅向量可以这样研究，许多别的知识也可以这样研究，如函数、指数函数、三角函数、数列等。这种教学不仅教了知识，也教会了学生如何思考。

3.2环节四 向量数量积的运算律

甲教师：

师：我们学习了向量的数量积，下面我们来学习向量的数量积的运算律。

（问题3）实数的运算满足哪些运算律呢？

生：交换律、结合律、分配律。

师：请同学们类比一下，向量的数量积满足交换律、结合律、分配律吗？

（学生计算、思考）3分钟后，

生：满足交换律，不满足结合律。

师：满足分配律吗？

生：应该满足吧。

师：为什么满足分配律，说说理由，你能证明吗？

生：……

师：好，大家类比一下实数的运算，应该是满足分配律的。现在大家还不会证明，是因为我们没有学向量的投影，现在我们来学习向量的投影。

（教师开始介绍向量的投影）

乙教师：

师：我们刚刚学习了一种新的运算——向量的数量积，学习了一种运算后，下一步我们应该研究什么？

生：研究它的性质。

师：哪些性质？

生：是否满足运算的交换律、结合律、分配律？

师：满足吗？

（学生计算、思考）

生：满足交换律，不满足结合律，分配律还不确定。

师：怎么不能确定？

生：不知道怎么证明。

师：那怎么办？不会证明，就没办法知道是否满足分配律吗？

生：能不能先用特殊的向量试试看？

师：对啊，你为什么不先试试看呢？

（学生用特殊向量计算、验证）

生：满足。

师：为什么满足？

生：我用好几个特殊的向量验证后都满足了。

师：那不特殊的向量也满足吗？你的结论具有一般性吗？

生：那得证明后才能知道。

师：好，我们下面就来证明这个结论。

教学意图

甲教师：教师通过设问，引导学生通过类比实数的运算律，证明向量的数量积所满足的运算律。

乙教师：引导学生回顾学习数学对象的过程，学习数学对象之后，应该学习数学对象的性质，对于在现阶段还不能证明的结论，以追问的形式引导学生用猜想、归纳、验证，最后进行演绎证明。

案例分析

数的运算、向量的线性运算、向量的数量积、矩阵的运算是一个发展趋势链，教学应该从发展的角度理解向量的数量积，引导学生认识到数、向量的运算联系，也为今后引入矩阵及其运算做了铺垫。

两位教师都能通过类比实数，学习向量数量积的运算律。甲教师是直接让学生去比较，乙教师则是引导学生经历“新的数学对象——对象的性质——（若可以进行运算）——运算法则”这一过程，这也是概念系统的建立过程，在这个过程中，学生能体会到研究数学的通法，这种教学就能促进学生主动地思考如何去研究数学对象。

当学生遇到困难，不会证明向量数量积的分配律时，甲教师是直接进行下一阶段的学习，通过补充新的知识来加以证明。乙教师则是引导学生从特殊到一般，先猜想、再验证、最后证明，这个过程也是数学新知识的发现过程，数学中的许多定理、结论都是这样发现的，如费马定理、庞加莱猜想、希尔伯特问题等，数学家们通过直觉思维猜想某个定理，再通过一些特殊的例子加以验证，最后以严密的方法进行逻辑证明。

当然，学生的发现与数学家的发现是不同的，学生是在教师引导下对知识的“再发现”，这种“再发现”可以帮助学生学会思考，思考解决问题的策略，乙教师的教学能引导学生经历这种“再发现”的过程。

4结束语

数学是思维的科学，数学的发展蕴含着丰富的思想方法，学生学习数学，不仅仅要学数学知识本身，还要学会像数学家一样思考。

数学教学是带领学生对数学知识进行“再创造”的过程，在这个过程中，学生感受数学知识的发生、发展，参与数学结论的发现，参与数学概念系统的创建，从而形成对数学完整的认识，发展理性思维。

教师不仅肩负着教学生知识的任务，更肩负着育人的使命。因此，在教学中如何呈现具体的数学知识，将科学的数学转换成具有教育任务的数学，使之能发挥培养学生思维的作用，是我们共同追求的理想。