数学历史发生法:概念及应用
2016-11-29徐伯华朱凤琴
徐伯华 朱凤琴
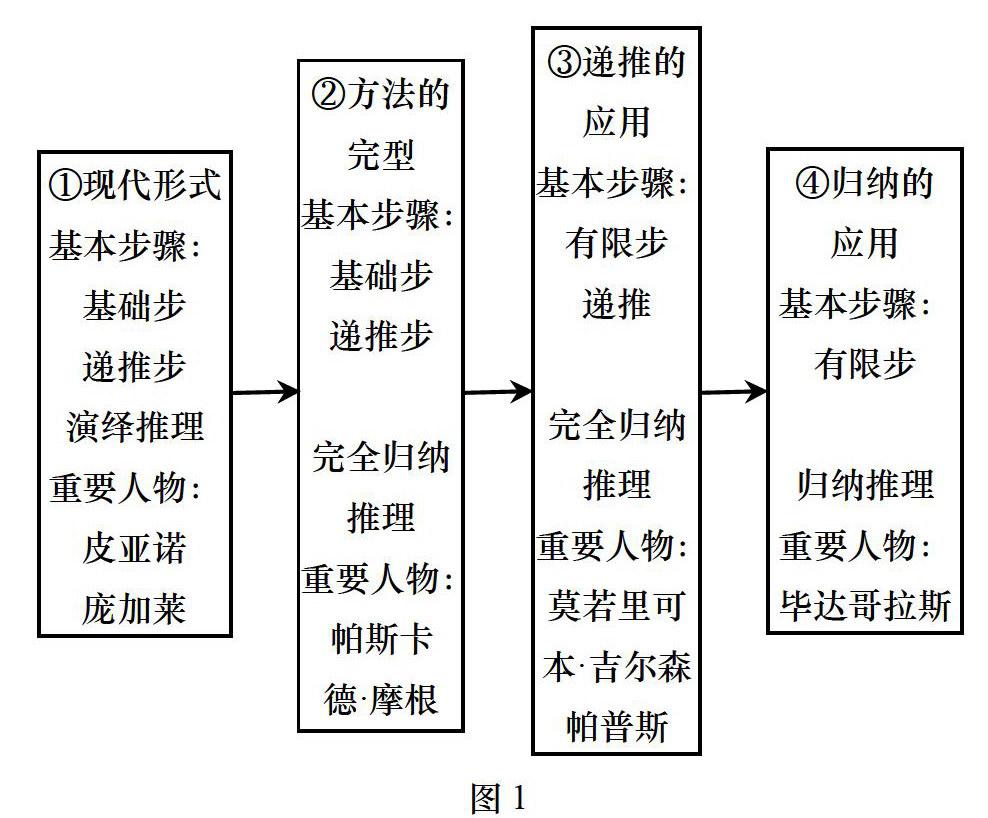
1历史发生法:探寻数学知识的历史发生规律
在HPM(数学史与数学教育)研究中,历史发生法是被广泛应用的发生学方法。所谓发生学方法(Genetics Methodology),“是在研究自然和社会现象时以分析它们的起源和发展过程为基础的一种研究方法”。发生学研究有两种取向:一是基于历史考查的历史发生研究,一是基于个体观察的个体发生研究。前者反映人类种族的认识发生,涉及的时问、区域、文化的跨度通常比较大,涉及的人物、事件及其影响通常是典型的、确定的甚至定论的,得到的结论更具有普遍性和规律性。后者反映人类个体的认识发生,时间、区域、文化的跨度通常很小,人物、事件及其影响可能是非典型的甚至是不确定的,结论更具有启发性和代表性。不过,很多人相信“种族的发展积淀为个体的发展,历史的过程以逻辑的形式保存在个体发生中”,这就在历史发生和个体发生之间架起了一座桥梁。因此,通过数学史的研究,寻求数学认识的发生发展规律,就能预见现在学生的数学认知,解决当前的数学教育问题,在很大程度上提高数学教学的效益。这种追本溯源、探索演变、寻求规律的研究方法就是历史发生法。
理解现在学生的数学认知和数学学习提供了有益的思路,一经提出就得到很多教育学家和数学教育家的支持。不过,历史发生原理毕竟是一个认识论假设,人们对它表现出四种态度:
(1)相信,直接的应用。典型代表是庞加莱、F·克莱因、A·Sfard等。如A·Sfard多次指出,数学史是分析、解释学生学习过程和学习困难的最宝贵资源,历史发生原理在同化、创造一个新概念时显得特别突出,已有的知识系统必须要经历一个完整的重建过程。还有美国学者表现得更坚决,“指导个体认知发展的最佳方式是让他重溯人类的认知发展,即使知识点A在逻辑上先于知识点B,但如果B在历史上先于A出现,那么我们仍应先教B”。
(2)原则上相信,批判的应用。典型代表是皮亚杰、维果斯基、波利亚、弗赖登塔尔等。如维果斯基认为,社会文化和环境会通过不同工具的使用改变人的思维活动,个体发生是由种族发生和社会历史条件共同决定的。弗赖登塔尔也清楚地指出,“我们不应该遵循发明者的足迹,而是经过改良同时有更好地引导作用的历史过程”,“从某种意义上说,儿童应该重蹈历史,尽管不是实际发生的历史,而是倘若我们的祖先己经知道我们今天有幸知道的东西,将会发生的历史”。
(3)检验,支持应用。自20世纪80年代开始,对历史发生原理的实证检验逐渐增多,几乎所有的检验结果都表明它是成立的。不过,历史发生原理毕竟难以获得完全的检验,不少人更愿意把它称为历史相似性原理,并支持在相似的意义下恰当地借鉴历史。
(4)质疑。20世纪90年代以后,质疑的声音时常出现。如A-Arcavi就对A-Sfard提出的“利用历史作为分析代数概念教与学的工具”给予质疑:“当年天才数学家对概念的理解过程,能帮助我们更好地了解现今学生的学习吗?”。K.Brating和J.Pejlare也指出,把数学的历史认识与学生的概念发展相提并论,会因为概念架构不同、默认观点不同、智力水平不同而产生严重的问题。
尽管有质疑,大家对历史发生原理的态度总体上还是积极的,尤其在数学史融入数学教学的研究中,正如Fauvel和Maanen所说:怎么用数学史?一方面是用数学史来了解并克服数学理解发展中的认识障碍,其中历史发生原理下的深刻分析是必要的;另一方面是把数学史当作一面镜子,在研究数学概念的发展中反映数学思想转变的机制,历史的视角与心理的视角相结合很值得重视。
运用历史发生原理考查数学归纳法的学习过程,学生也应该经历从不完全归纳到直觉的完全归纳、再到演绎的完全归纳的认识路线,其中可能会遇到从不完全归纳到完全归纳的困难、从有限到无限的困难、构建递推步的困难、认识归纳原理的困难等,而要化解这些困难,需要让学生很好地理解无穷的思想、递推的思想、不完全归纳法、完全归纳法、演绎法、归纳公理。但是,从学生的心理发展水平看,归纳公理和无穷的思想具有很强的基础性,对高中生的要求不宜太高,应把重点放在完全归纳的理解、递推步骤的构建和方法的适用条件上。
3历史发生教学法:依据学生数学发生设计课堂教学
发生教学法是与公理化教学法相对的,前者注重数学知识的认识发生过程,后者注重形式演绎过程。由于人的认识总是从简单到复杂、从具体到抽象,所以公理化教学法违背了人的认识规律。新数运动的失败也证明公理化教学法不符合学生数学学习的实际。而发生教学法不把数学知识视为既定的结果,而是促进学生去数学发现,这就容易引起学生的意识活动,因此能够提高学生的数学理解水平和数学认识能力。
教学法是对教学要素的组织方式。历史发生教学法就是根据某个数学知识的历史发生规律,考虑学生个体的认知过程和关键环节,通过适当的教学法加工,促进学生数学认知的发生发展,化解可能遇到的困难,提供有用的教学资源,设计出有助于学生数学学习的教学方案。
1963年,托普利茨出版《微积分:发生原理》,标志着“发生教学法的思想最终形成”。作者把数学史作为教学的指南,主张从数学史中获取概念发展的关键方式,在朴素水平上就开始教授本质的观念,然后是较低水平的应用,然后是深入到背景的解释和应用,在学生获得概念的意义之后,再逐步增加概念的精确性和严密性,很好地应用了微积分的历史发生过程和规律。
历史发生教学法有多种形式,可以用数学史不谈数学史,或者用数学史也谈数学史,还可以把数学史和数学方法论、数学哲学、数学文化结合起来使用。在HPM实践中,以下两种模式是比较典型的:
(1)台湾师范大学苏意雯博士提出的三面向模式。即在认识论和自我诠释理论指导下,把数学知识的逻辑分析、历史分析和心理分析结合起来,通过学习单的设计和实施,使教学内容和形式既能适应学生的认知水平和课程目标,又能提高学习兴趣、增强数学体验、发展数学能力。主要操作步骤是:①体会教科书编者、课程标准与教科书内容;②体会古代数学家、数学知识、数学理论之精神;③考虑学生需求,编制学习单;④课堂教学。
(2)华东师范大学汪晓勤团队提出的历史发生原理工程化。即以Gmssman学科教学知识框架和认知的历史发生原理为基础,通过研读数学史,获得关于特定课题的学科性质知识、学科本质知识、课题来源及发展的知识、学生理解和误解的知识以及数学课程与教材的知识等,再结合课堂和学生的实际,组织特定的教学策略和知识表征。主要操作步骤是:①了解所教主题的历史;②理解该主题历史进化的关键步骤;③在现代情境下重构推动进化的关键思想或问题,使之适合介绍新知;④从易到难给出上述重构的问题系列;⑤课堂教学。
关于数学归纳法的教学分析和设计,可参考文献,不再赘述。
