含三个含时点接触的量子输运

程 芳

(长沙理工大学物理与电子科学学院，中国 长沙 410004)



含三个含时点接触的量子输运

程 芳*

(长沙理工大学物理与电子科学学院，中国 长沙 410004)

拓扑绝缘体的材料可大大提高计算机芯片的运行速度和工作效率，甚至可能会成为以自旋电子学为基础的下一代全新计算机技术的基石．拓扑绝缘体的边缘态展现出奇特的性质，电子在表面自由流动，不损耗任何能量．使用玻色化，重整化群，格林函数的方法从理论上研究了三个含时点接触存在对拓扑边缘态输运性质的影响．得到电流随偏压和温度变化的解析表达式，以及依赖于电子间相互作用幂指数变化规律．该理论提供了一种调控纳米结构中输运性质的手段．

拓扑绝缘体；含时点接触； 拉廷格液体；量子输运

全电操纵的自旋电子学器件的制备和性能研究是当今凝聚态物理领域的前沿研究课题[1-2]．拓扑绝缘体是现代凝聚态物理中的一个重要研究主题．拓扑绝缘体不是常规的超导体，它只能携带很小的电流，不能用于超高效电源线，但它为微芯片开发的范式转移铺平了道路，这将导致自旋电子学的新应用，即利用电子自旋来携带信息．从电子能带结构上来说，拓扑绝缘态不能用传统的金属、绝缘体来描述，而是一种全新的物质态．它的体电子态是有能隙的绝缘态，但它的表面(对三维体系)或者边缘(对二维体系)电子态则是零能隙有手性的金属态[3-7]．螺旋的表面电子态具有线性色散关系并且自旋与动量满足特定的手性关系．由于其独特的能带结构和手征特性，电子的输运、磁学和光学性质将明显不同于普通体系[8-13]． 这个快速成长的领域中的关键问题之一是如何检测和控制的拓扑边缘态．到目前为止，量子自旋霍尔坝的边缘态已经通过直流偏压下测量源极和漏极之间电导检测到．最近，文献[14-17]提出使用量子点接触，即带间耦合， 来控制边缘态的输运．量子霍尔效应不是唯一的拓扑绝缘体，最近物理学家陆续预言并实验发现了一系列二维材料由于其自身的自旋轨道耦合导致新的拓扑绝缘态．在该类材料中，自旋轨道耦合会在体能带打开一个带隙分开完全占据的价带和空的导带，并在带隙里面建立起边缘态．量子自旋霍尔边界状态有重要的自旋过滤性质，它可以使自旋向上的电子向一个方向传播，而使自旋向下的电子向另一个方向传播．类比于一种螺旋型粒子的自旋和动量间的关系，后来把这种边界状态称作“螺旋形状态”．

1 螺旋Luttinger 液体的哈密顿量

螺旋Luttinger 液体的自旋与动量方向锁定的，只有准一维系统一半的自由度．考虑一个由右移自旋向上，左移自旋向下的螺旋Luttinger 液体[18]．由于时间反演对称性，单粒子的背散射过程被禁止．自由电子的哈密顿量

同一分支两个电子散射产生的哈密顿量

不同分支两个电子散射产生的哈密顿量

一般忽略倒逆 (umklapp)散射，因为这个过程只在commensurate fillings变得重要．其中λ2和 λ4是相互作用的常数．定义共轭玻色相场 φ=ΦR↑+ΦL↓,θ=ΦR↑-ΦL↓,得到玻色化后系统总的哈密顿量 H=H0+Hch+Hfw.

我们研究含三个量子点接触的自旋霍尔体系，系统示意图如图1所示.自旋守恒的隧穿哈密顿量

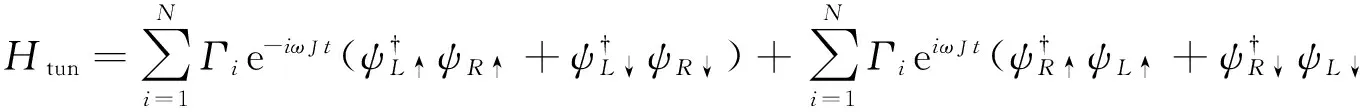
2 隧穿电流

总电流 I=〈j(t)〉 由直流和交流两部分组成，现实体系中频率 Ω 很高，因此我们通常计算隧穿电流在一个周期内的平均值，也就是隧穿电流的直流部分．

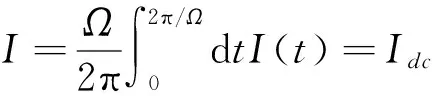
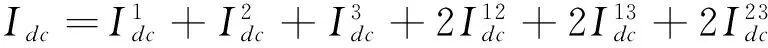
2.1 温度T=0情形

隧穿电流的直流部分的表达式为

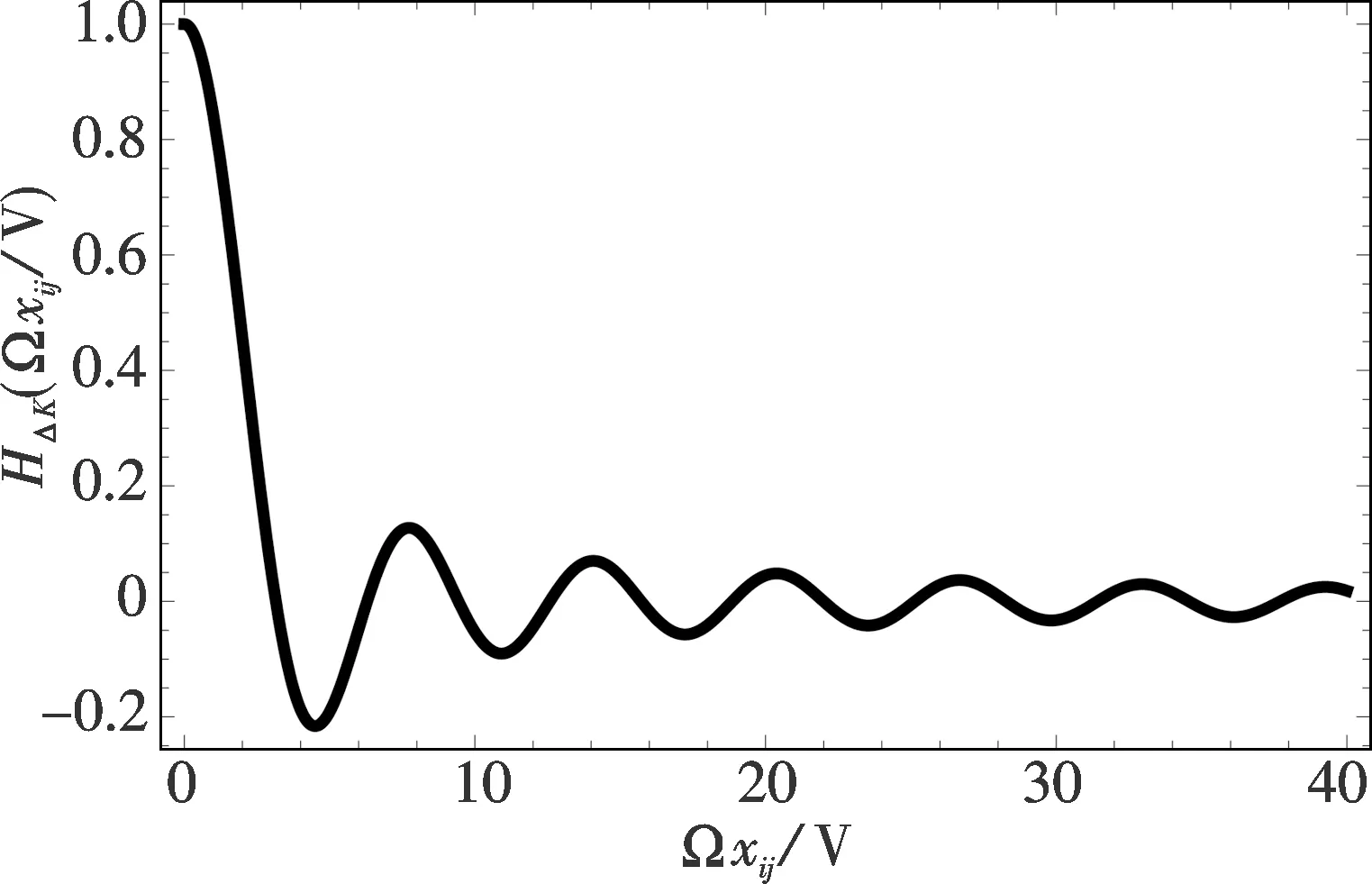
图2 函数H随频率的变化关系，其中K=0.9Fig.2 H as a function of the frequency for a fixed interaction-strengths K=0.9

其中 xij=xi-xj表示两个量子点接触的空间距离；φij=φi-φj表示施加在两个量子点接触上含时电压的相位差．

隧穿泵电流，(ωJ=0)，我们研究了H函数随频率的变化关系，结果如图2所示.

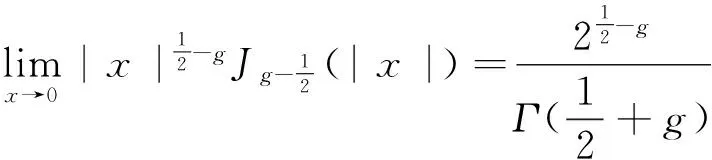
2.2 温度T≠0情形

单个点接触情况隧穿电流的直流部分为

其中B是欧拉beta函数．

隧穿泵电流，也就是当V=0电流的表达式为

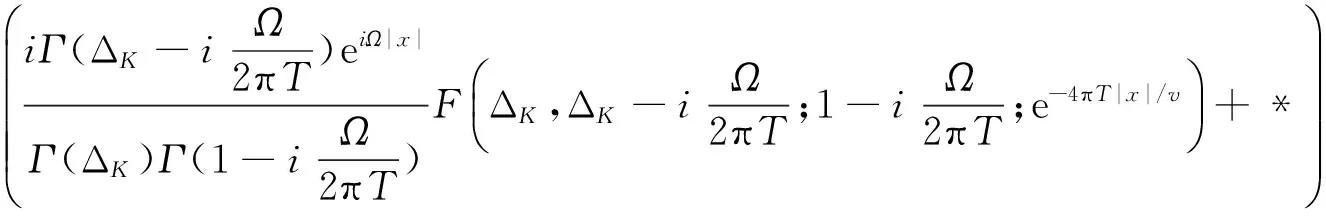
我们研究了在不同参数范围内，泵浦电流随频率Ω的变化关系式，见表1.

表1 在不同的参数范围内，泵浦电流随频率Ω的变化关系

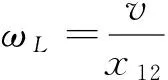
3 结论

采用玻色化、重整化群及格林函数的方法从理论上研究了3个含时点接触存在对拓扑边缘态输运性质的影响．得到泵浦电流随偏压和温度变化的解析表达式，以及依赖于电子间相互作用幂指数变化规律．研究结果提供了一种调控纳米结构中输运性质的手段．

[1] WOLF S A,AWSCHALOM D D,BUHRMAN R A,etal.Spintronics: a spin-based electronics vision for the future [J].Science,2001,294(16):1488-1495.

[3] QI X L,ZHANG S C.The quantum spin Hall effect and topological insulators [J].Phys Today,2010,63(1):33.

[4] HASAN M Z,KANE C L.Topological insulators [J].Rev Mod Phys,2010,82(4):3045-3067.

[5] MOORE J E.Perspective article the birth of topological insulators [J].Nature,2010,464(6):194-198.

[6] SHI L,ZHANG S C,CHANG K.Anomalous electron trajectory in topological insulators [J].Phys Rev B,2013,87(5):161115.

[7] CHEN M N,SHENG L,SHEN R,etal.Spin Chern pumping from the bulk of two-dimensional topological insulators [J].Phys Rev B,2015,91(12):125117.

[8] SHENG D N,WENG Z Y,SHENG L,etal.Quantum spin-hall effect and topologically invariant chern numbers [J].Phys Rev Lett,2006,97(3):036808.

[9] FU L,KANE C L,MELE E J.Topological insulators in three dimensions [J].Phys Rev Lett,2007,98(11):106803.

[10] BERNEVIG B A,HUGHES T L,ZHANG S C.Quantum spin hall effect and topological phase transition in HgTe quantum wells [J].Science,2006,314(6):1757.

[11] CHANG K,LOU W K.Helical quantum states in HgTe quantum dots with inverted band structures [J].Phys Rev Lett,2011,106(2):206802.

[12] MIAO M S,YAN Q,WALLE C G,etal.Polarization-driven topological insulator transition in a GaN/InN/GaN quantum well [J].Phys Rev Lett,2012,109(8):186803.

[13] ZHANG D,LOU W K,MIAO M,etal.Interface-induced topological insulator transition in GaAs/Ge/GaAs quantum wells [J].Phys Rev Lett,2013,111(7):156402.

[14] STRÖM A,JOHANNESSON H.Tunneling between edge states in a quantum spin hall system [J].Phys Rev Lett,2009,102(9):096806.

[15] SCHMIDT T L.Current correlations in quantum spin hall insulators [J].Phys Rev Lett,2011,107(9):096602.

[16] TEO J C Y,KANE C L.Critical behavior of a point contact in a quantum spin Hall insulator [J].Phys Rev B,2009,79(23):235321.

[17] ZHANG L B,CHENG F,ZHAI F,etal.Electrical switching of the edge channel transport in HgTe quantum wells with an inverted band structure [J].Phys Rev B,2011,83(8):081402(R).

[18] RONETTI F,VANNUCCI L,DOLCETTO G,etal.Spin-thermoelectric transport induced by interactions and spin-flip processes in two-dimensional topological insulators [J].Phys Rev B,2016,93(16):165414.

(编辑 CXM)

Quantum Transport with Three Time Dependent Quantum Point Contacts

CHENGFang*

(Department of Physics and Electronic Science,Changsha University of Science and Technology,Changsha 410004,China)

The novel topological insulator material has provided the physical foundation for the dissipationless spin transport,possibly constructed the brand-new spintronic devices.The edge state of the topological insulator shows unusual helical feature due to the electron spin-momentum locking.Using the Luttinger liquid theory and nonequilibium Green function,the quantum transport in a quantum spin Hall bar with three quantum point contacts (QPCs)was studied.The currents display very different pump frequency dependence for weak and strong e-e interaction.These unique properties were induced by the helical feature of the edge states,and therefore can be used to detect and control edge state transport.

topological insulator; time dependent quantum point contacts; Luttinger liquid; quantum transport

10.7612/j.issn.1000-2537.2016.05.010

2016-07-12

国家自然科学基金资助项目(11374002)

*通讯作者,E-mail：277165900@qq.com

O413.2

A

1000-2537(2016)05-0061-04