车载作用下矮塔斜拉桥拉索疲劳性能研究

陈泽

（长沙理工大学土木与建筑学院，湖南长沙 410004）

车载作用下矮塔斜拉桥拉索疲劳性能研究

陈泽

（长沙理工大学土木与建筑学院，湖南长沙 410004）

以国内某矮塔斜拉桥为研究背景，在假定“疲劳车”交变应力作用下，利用MIDAS/Civil对该桥模型进行车辆荷载移动时程分析，得到恒载及活载共同作用下拉索的时变应力；依据疲劳线性累积损伤理论，证明了仅在车载作用下矮塔斜拉桥拉索的应力幅非常小，能经历规范规定的200万次循环荷载作用而不会发生疲劳破坏。

桥梁；车辆荷载；部分斜拉桥；斜拉索；疲劳性能

与其他斜拉桥相比，矮塔斜拉桥的塔高降低一半以上，梁的刚度增大，其受力特点是斜拉索承担约30%的荷载。因此，斜拉索在车载、风载等活载的共同作用下容易产生疲劳损伤，当损伤累积达到一定程度时将会发生疲劳破坏。由于条件限制，该文仅对车载作用下国内某矮塔斜拉桥拉索的疲劳性能进行研究。

1 工程概况

某五跨四塔矮塔斜拉桥，桥跨布置为128 m+3 ×210 m+128 m。其主要技术标准为：双向六车道高速公路；公路-Ⅰ级设计荷载；设计行车速度100km/h；地震动峰值加速度为0.05g。主桥桥型布置见图1。

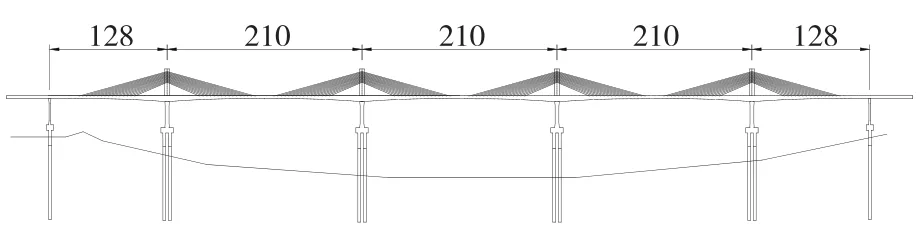
图1　主桥桥型布置示意图（单位：m）

采用MIDAS/Civil建立该桥模型，全桥结构分为主墩、基础、主塔、主梁、斜拉索五部分，斜拉索在主塔上的连接以刚性连接进行建模；主梁上为了更好地模拟车辆荷载，结构中选择以无重量及刚度为无穷大的虚拟梁进行连接。全桥由782个节点和839个单元组成（见图2）。

图2　大桥有限元模型

2 疲劳荷载谱的获取

2.1车载作用下拉索的时变应力

斜拉索常年裸露在外，在车载、风载等活载作用下易发生疲劳破坏。这里只对拉索疲劳影响最大的车载进行研究。当车辆按照一定的速度驶过桥面时，其对斜拉索产生的作用随着时间改变。要输入全部桥面节点随时间改变的荷载，工作量非常大，且不必要。该文要研究的是车载作用下拉索的疲劳问题，只要按拉索的内力影响线在其受力较大的桥面节点位置输入车辆时变荷载即可。该桥是对称的，故选取1、2号主塔的斜拉索（单元号576～639）为研究对象。1、2号主塔斜拉索单元号见图3，拉索内力影响线见图4和图5。

图3　1、2号主塔斜拉索单元号示意图

图4　576号单元内力影响线

图5　639号单元内力影响线

根据单元内力影响线，1、2号主塔斜拉索影响最大的位置为各跨跨中位置，并且塔根处车载对斜拉索内力的影响极小，可不考虑。因此，只需输入各跨跨中位置附近各桥面节点的时变荷载。

为简化起见，把1辆主车简化成1个集中荷载，1辆重车简化成2个集中荷载。将主车和重车组成一列车队，该车队中重车数为1辆，各主车之间的距离为20 m，并匀速（v=20 m/s）行驶（见图6）。

图6　简化车辆荷载示意图（单位：荷载为k N，其他为m）

该桥设计为双向六车道，考虑横、纵向折减系数（分别为0.55、0.97）和动力系数μ，各个数据乘以0.55×0.97×（1+μ）×2=0.55×0.97×1.05×2= 1.12即可将其转换为六车道车辆荷载。通过各桥面节点的时程函数将车辆随时间变化的荷载作为节点动力荷载输入模型，对模型进行移动时程分析，得到斜拉索在该车列经过桥面时的时变应力。1、2号主塔上斜拉索的时变应力见图7～10。

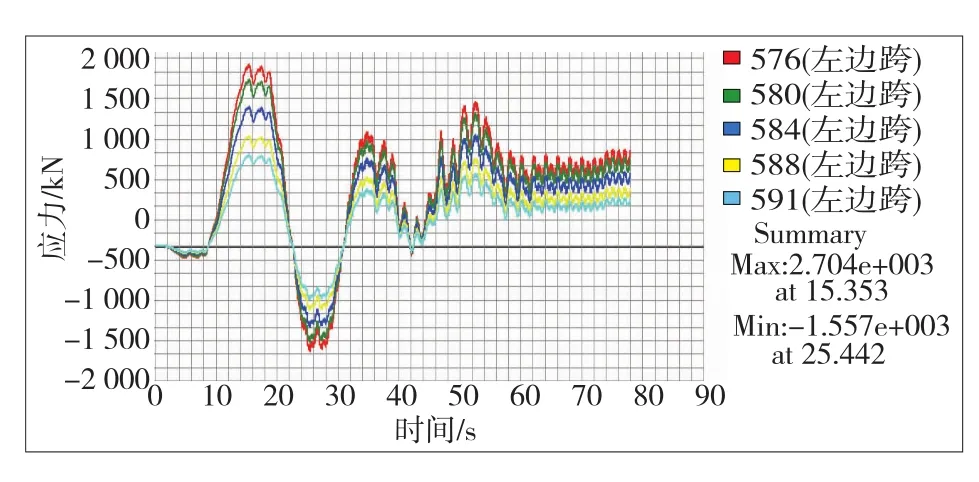
图7　1号主塔左侧斜拉索时变应力曲线

图8　1号主塔右侧斜拉索时变应力曲线

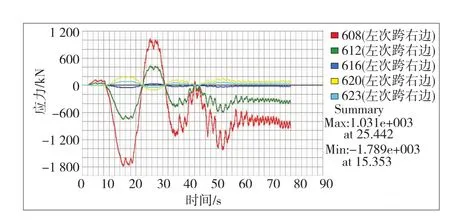
图9　2号主塔左侧斜拉索时变应力曲线

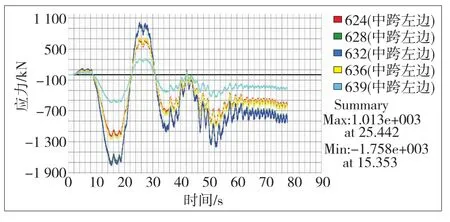
图10　2号主塔右侧斜拉索时变应力曲线

2.2恒载及活载共同作用下拉索的时变应力

以上斜拉索的时变应力只考虑了车载的作用，而车载对斜拉索应力的影响不是最大的，最主要的是恒载作用。把荷载作用下的常幅应力与车载作用下的交变应力叠加，可得到斜拉索的疲劳交变应力。选取对疲劳影响最大（应力幅最大）的602号斜拉索进行研究，其应力时程曲线见图11。

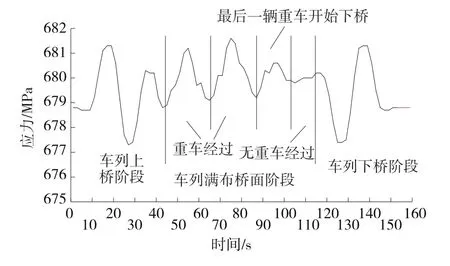
图11　602号斜拉索应力时程曲线

3 矮塔斜拉桥拉索的疲劳性能分析

当一列车队经过桥面时，602号斜拉索的损伤度见表1。因没有详尽的斜拉索在不同应力比下模拟试验的S-N曲线，根据GB 50017-2003《钢结构设计规范》第6.2.1条的规定，对于无连接处的主体金属，其参数C=1 940×1012、β=4，则根据N= C/（Sa为应力幅；m=β=4）可得到破坏循环次数Ni。

表1中模拟的是一列车队中只有1辆重车，实际上重车的数量在一列车队中是随机的。使用MATLAB软件随机生成1组均值为2、标准差为3的数列，除去该数列的负数随机数，取该数列前100个随机数列作为一列车队中重车数量的随机数列，得该100列车队中重车总数为144辆，含有重车的车列为72列。当前100列车队驶过桥面时，602号斜拉索的损伤度见表2。

按照疲劳线性累积损伤理论，当第100列车之后的车列驶过桥面时，各个车列对斜拉索的损伤度可以按前100次总损伤度的1%来计算。设总的车队列数为N，则第100列车队以后602号斜拉索的损伤度总和为（N-100）×（2.58×10-11）/100。按照疲劳破坏的极限状态方程，取累计损伤度a= 1，则可求出602号斜拉索能够经历的车队列数：

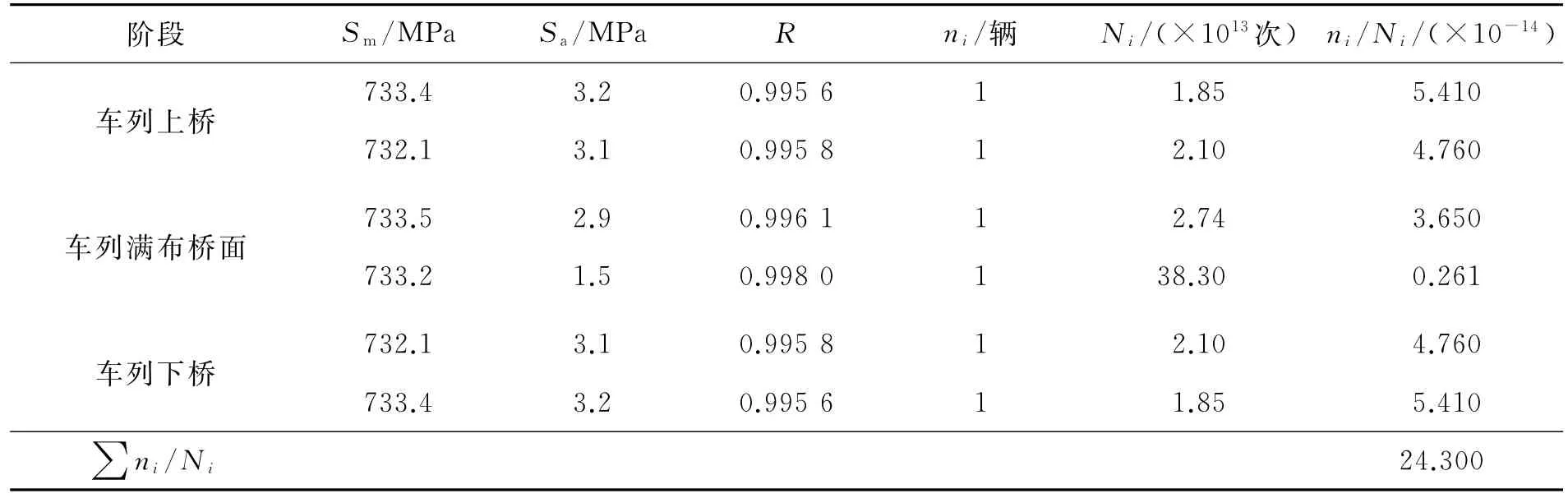
表1　一列车队经过桥面时602号斜拉索的损伤度

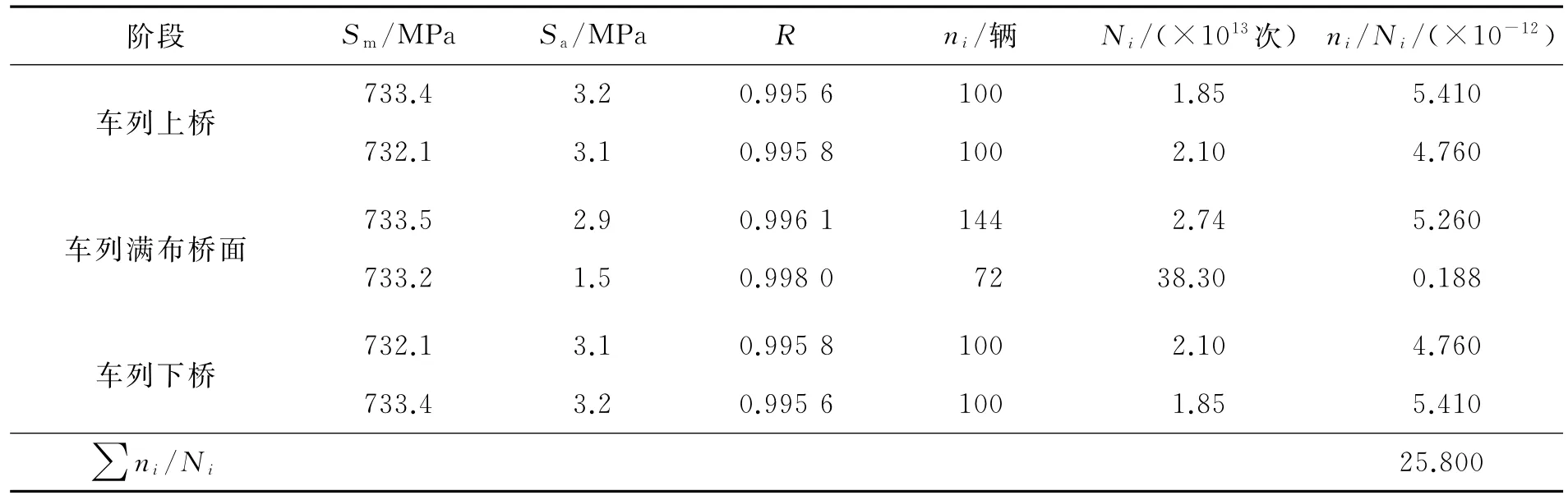
表2　前100列车队经过桥面时602号斜拉索的损伤度

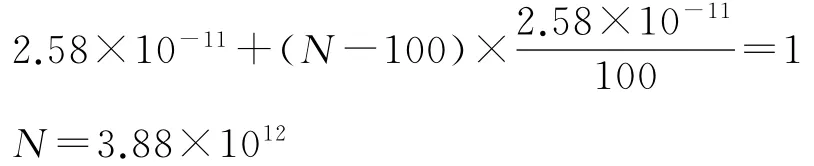
4 结论

在假定“疲劳车”交变应力作用下，该矮塔斜拉桥拉索最少能经历1012次应力循环，远远超过规范中规定的2×106次应力循环，不会发生疲劳破坏。表明仅在车载交变应力作用下，矮塔斜拉桥拉索的应力幅非常小，也说明矮塔斜拉桥设计时拉索应力强度按0.6σu（拉索的抗拉标准强度）设计合理。

［1］ 杨美良，李波，张建仁.车辆荷载作用下部分斜拉桥拉索疲劳可靠度研究［J］.公路交通科技，2007，24（12）.

［2］ 何震.部分斜拉桥车载疲劳研究及索塔锚固分析［D］.武汉：华中科技大学，2007.

［3］ 刘扬，杨刚，马宁，等.车辆荷载下长山大桥斜拉索以及塔梁墩连接处疲劳分析［J］.大连海事大学学报，2015，41（2）.

［4］ 邱敏，高宁妥，覃巍巍，等.三官汉江矮塔斜拉桥索塔节段模型试验研究［J］.预应力技术，2014（5）.

［5］ 孙向东.江肇高速西江大桥宽幅脊梁矮塔斜拉桥设计［J］.公路，2010（5）.

［6］ 刘沐宇，涂开智，孙向东，等.基于疲劳可靠度矮塔斜拉桥拉索容许应力分析［J］.武汉理工大学学报，2009，31（14）.

［7］ 朱殷桥，姚国文.钢绞线腐蚀疲劳试验方法与损伤评定研究［J］.公路与汽运，2014（2）.

［8］ 郑万山，唐光武，郑罡，等.苏通大桥斜拉索拉弯疲劳试验研究［J］.公路交通技术，2010（4）.

［9］ 胡晓.随机车流作用下大跨度斜拉桥振动响应分析［D］.长沙：长沙理工大学，2013.

［10］ JTG D60-2004，公路桥涵设计通用规范［S］.

U448.27

A

1671-2668（2016）05-0156-03

2016-03-14