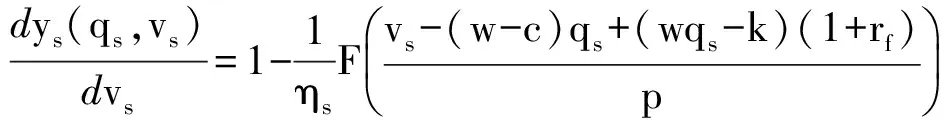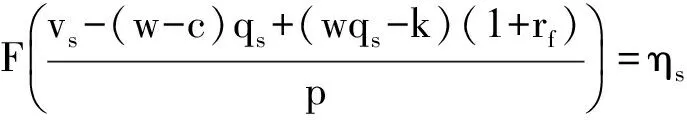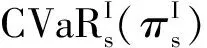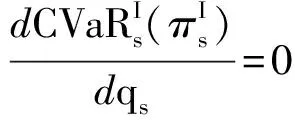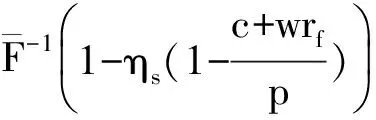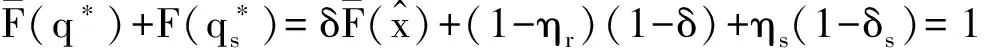基于η-CVaR准则的供应链金融回购契约协调策略

刘重庆，晏妮娜

(中央财经大学 商学院，北京 100081)



基于η-CVaR准则的供应链金融回购契约协调策略

刘重庆*，晏妮娜

(中央财经大学 商学院，北京 100081)

在条件风险价值(CVaR)的风险度量准则下，设计了一个由生产商、受资金约束的零售商和银行组成的供应链金融系统.同时考虑生产商和零售商的风险偏好，研究回购契约下供应链金融的融资与运营决策及其协调策略，得出了各个主体的最优决策.研究了生产商风险偏好、零售商风险偏好和回购价格对最优决策的影响，并分析了分散决策与集成决策的协调性.研究发现，分散供应链的最优决策可以与集成供应链的最优决策保持一致，甚至出现超协调效应.最后，通过数值算例验证该文的研究结果.

供应链金融； 风险偏好； 条件风险价值； 回购契约； 协调

近年来，供应链金融(Supply chain finance，SCF)运营风险与融资决策备受关注.2014年，爆发的青岛港“德正系”仓单重复质押骗贷案中，数十家中外银行受牵连，涉案金额45亿美元左右.可见，供应链金融面临的风险对其经营具有重大影响，研究不同决策主体的风险偏好具有重要意义.对于现实中的融资企业，尤其是中小型零售商，由于信贷条件较差，很难从银行及时筹措资金.而回购契约是一种解决中小企业融资问题的方法，如何实现回购契约下供应链金融的有效协调，也是值得关注和研究的问题.

关于供应链中风险特征的研究已有大量文献.Schweitzer 和Cachon对比了采购经理的实际订购量与期望利润最大化计算的订购量，两者不一致[1].采购经理的风险偏好会影响其决策.近年来许多供应链库存管理的研究都开始采取决策者风险偏好的观点[2].此后，利用条件风险价值(CVaR)研究供应链风险决策的成果大量涌现[3-6].还有学者将CVaR和期望利润最大化等方法结合起来，如构建CVaR和期望利润的均衡模型来分析风险规避的传统库存决策[7].

最近，供应链协调的研究取得了丰厚的成果.王新辉和汪贤裕考虑了销售商的风险特征，而没有研究供应商的风险特性[8].Wei和Choi设计了批发定价和利润分享计划来协调均值——方差风险测度下的供应链[9].“Target Sales Rebate”契约[10]和多期模型[11]也可用于协调供应链的库存和价格策略.收益共享契约和回购契约下的供应链协调策略也曾有报道[12-13].Yan和Sun研究了有限融资方案下的供应链金融系统的协调性[14].与其不同的是，本文在回购契约下同时考虑了生产商和零售商的风险偏好.

上述研究大都针对生产商和零售商组成的传统二级供应链，且很少同时考虑生产商和零售商的风险偏好，也缺乏对回购契约下供应链金融的协调分析.基于此前研究基础，本文同时考虑了生产商和零售商的风险偏好，基于η-CVaR准则研究了回购契约下供应链金融系统的协调性.

1 模型描述

1.1 变量定义与假设条件

表1 变量符号

注：r、m、b分别表示零售商、生产商、银行的决策，*表示最优决策.

1.2 决策时序与模型框架

生产商首先制定批发价格w，然后零售商确定订购量q，并根据融资缺口确定向银行的借款额wq-k，银行制定贷款利率r.销售期末，如果零售商实现的收益能够足额偿还借款本息，则银行收回贷款本息(wq-k)(1+r)；否则，生产商按照价格b回购零售商的库存量q-x，零售商因回购而取得收益b(q-x)，从而降低了银行的贷款损失.生产商和零售商分别作为主方和从方进行动态博弈，风险中性的银行与生产商和零售商组成的子系统进行静态博弈.决策模型框架如图1所示.

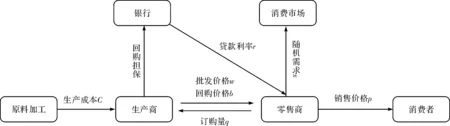
图1 供应链金融系统框架Fig.1 Framework of supply chain finance system

2 均衡分析

2.1 风险中性型银行的最优决策

如果零售商期末能够偿还借款本息，则银行全额收回贷款本息(wq-k)(1+r)；否则，生产商将回购零售商的库存商品，假设理性的生产商不会通过回购使零售商获取超额的利润，零售商将其收益px+b(q-x)全部用于偿还债务.

银行期末获得的利润可表示为：

完全竞争的资本市场中，银行进行决策时是使期望利润为零，即E(πb)=0.因而，银行的决策问题可表示为(1)式：

(wq-k)(1+rf) .

(1)

命题1 由(1)式可直接得出银行的最优贷款利率决策，即

银行最优贷款利率随着其自有资金成本率的增加而增加.而且最优贷款利率与回购价格密切相关，具体关系可表述为推论1.

最优贷款利率和回购价格之间存在着递减关系.回购价格越高，意味着生产商分担了更多的零售商破产风险，银行承担的风险降低，因而银行制定的最优贷款利率就越低.

2.2 风险偏好型零售商的最优决策

零售商风险偏好系数是ηr，基于CVaR准则，零售商所面临的决策问题如(2)式所示.

MaxCVaRr(πr)=

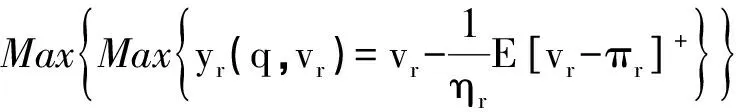
(2)

其中，yr(q，vr)是一个凹函数.根据CVaR模型的定义式可以得出，

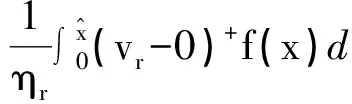
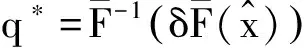
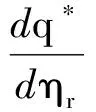
零售商的最优订购量随着其风险偏好程度的增加而增大，也就是说如果零售商越规避风险，那么就会减少订购量.

2.3 风险偏好型生产商的最优决策

当零售商期末实现的销售收益能够还清贷款本息时，就谈不上生产商回购的问题，生产商可以获得稳定收益(w-c)q；否则，生产商就会以价格b回购零售商的库存商品，此时生产商的利润为(w-c)q-b(q-x).生产商期末的利润可以表示为：

生产商风险偏好系数为ηm，基于CVaR准则，生产商所面临的决策问题为(3)式.

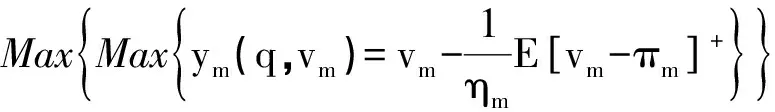
(3)

其中，ym(q，vm)是一个凹函数，根据CVaR模型的定义式可以得出，

命题3 考虑最优贷款利率r*和零售商最优订购量q*，生产商的最优批发价格w*应满足：

生产商最优批发价格受其风险偏好系数、回购价格的影响.只有当生产商风险偏好系数大于或等于零售商破产风险时，生产商的风险偏好系数才会对其批发价格产生影响.而回购价格总会对最优批发价格产生影响，回购价格越大，意味着生产商承担了更多的风险，那么它就会制定更高的批发价格.

3 协调分析

3.1 集成决策

集成决策时的预期利润为：

(wqs-k)(1+rf).

(4)

根据CVaR模型的定义式可知ys(q，vs)满足：

(wqs-k)(1+rf))f(x)dx-

(wqs-k)(1+rf))f(x)dx.

可见，ηs越小，集成决策时的最优订购量就会越小.这种情况下，分散决策时的最优订购量就有可能与集成决策时的最优订购量保持一致.

3.2 协调策略

批发价格和回购价格等因素会对最优订购量产生影响，而且生产商和零售商的风险偏好系数也会对协调策略产生重大影响，这是本文与传统研究的区别之一.分散决策时的最优订购量受生产商和零售商的风险偏好系数的影响，集成决策时的最优订购量受系统风险偏好系数取值的影响.系统的风险偏好特性将使集成最优决策发生重大变化，供应链金融分散系统与集成决策有可能实现协调.

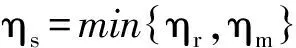
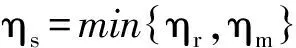
在协调机制中，以生产商和零售商风险偏好系数的较小者代表集成决策时的系统风险偏好系数，系统的风险规避特性将导致集成决策时的最优订购量降低.此外，生产商的回购策略促进了分散决策时最优订购量的扩大.集成决策时最优订购量的降低和分散决策时最优订购量的扩大使协调得以实现.

4 算例分析

本部分结合数值算例进行模型检验.假设随机需求满足均值为50的指数分布，单位生产成本c=0.3，单位零售价格p=2，银行自有资金成本率rf=0.05.

4.1 零售商风险偏好的影响

图2表明，零售商的最优订购量和其风险偏好系数之间存在着递增关系，验证了本文的推论2.图3表明，最优批发价格和零售商风险偏好系数之间存在着递减关系.如果ηr越大，说明零售商愿意承担更多的风险，那么生产商就会制定较低的批发价格以激励零售商扩大订购量.图4表明，最优贷款利率和零售商风险偏好系数之间存在着递增关系.ηr越大，零售商需要的融资额就会提升，银行面临的贷款风险就会提高，因而银行会提高贷款利率.

图2 零售商风险偏好对订购量的影响Fig.2 The effect of retailer’s risk preference on orders

图3 零售商风险偏好对批发价格的影响Fig.3 The effect of retailer’s risk preference on wholesale price

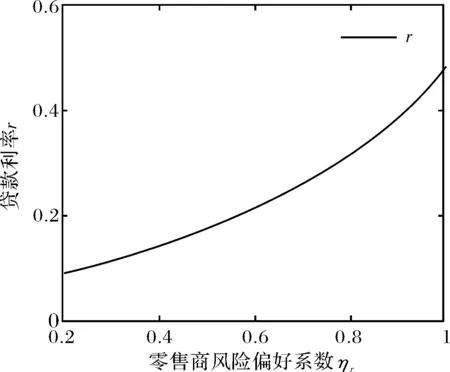
图4 零售商风险偏好对贷款利率的影响Fig.4 The effect of retailer’s risk preference on interest rate

4.2 生产商风险偏好的影响

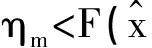
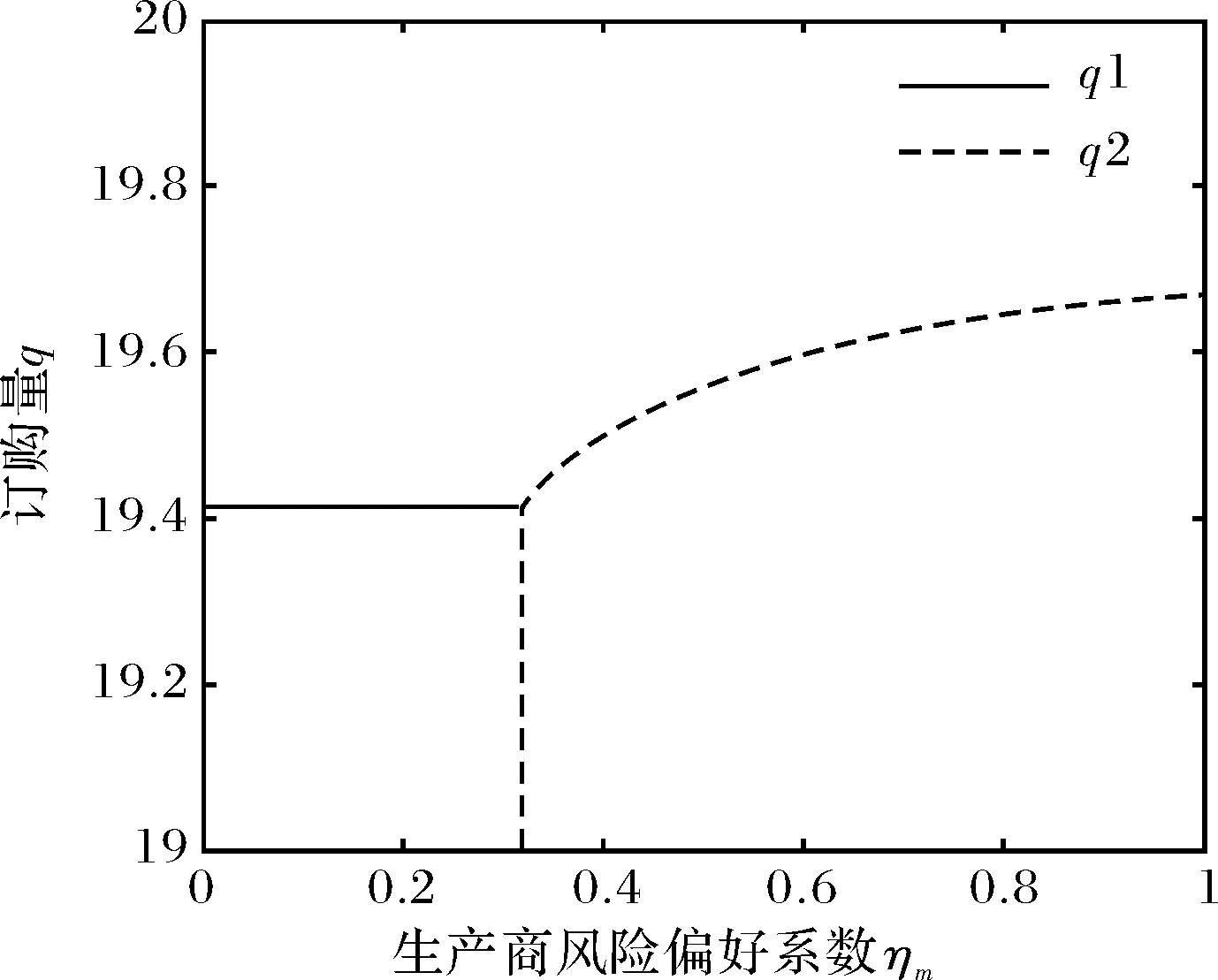
图5 生产商风险偏好对订购量的影响Fig.5 The effect of manufacture’s risk preference on orders

图6 生产商风险偏好对批发价格的影响Fig.6 The effect of manufacture’s risk preference on wholesale price

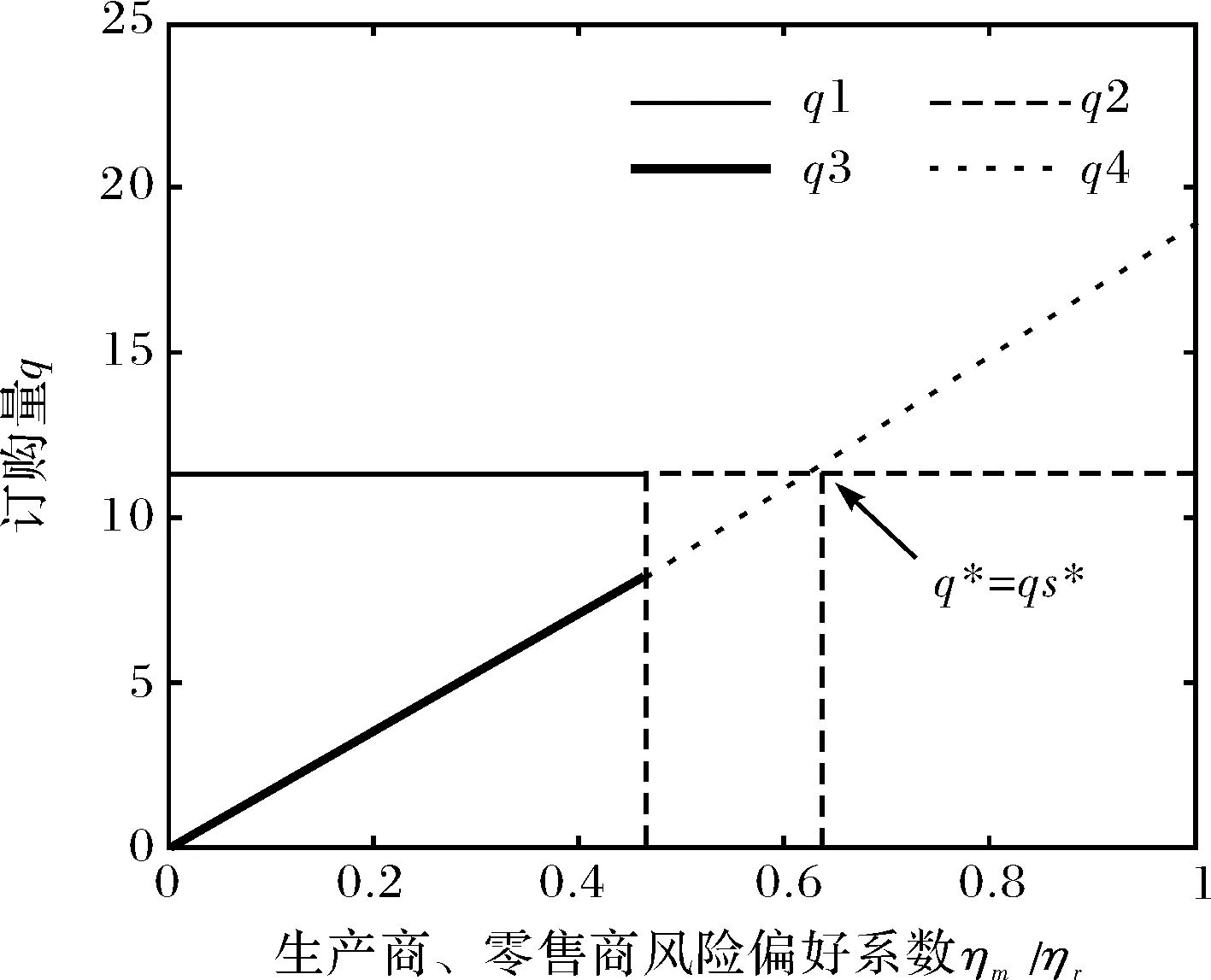
图7 生产商、零售商风险偏好系数与协调分析Fig.7 Manufacture’s and retailer’ risk preference and coordination analysis

4.3 回购价格的影响

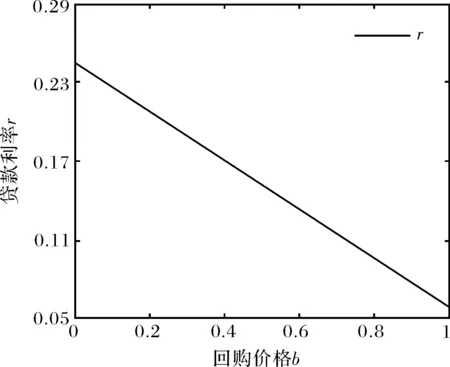
图8 回购价格对贷款利率的影响Fig.8 The effect of buy-back price on interest rate

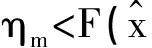
图9 回购价格对订购量的影响Fig.9 The effect of buy-back price on orders

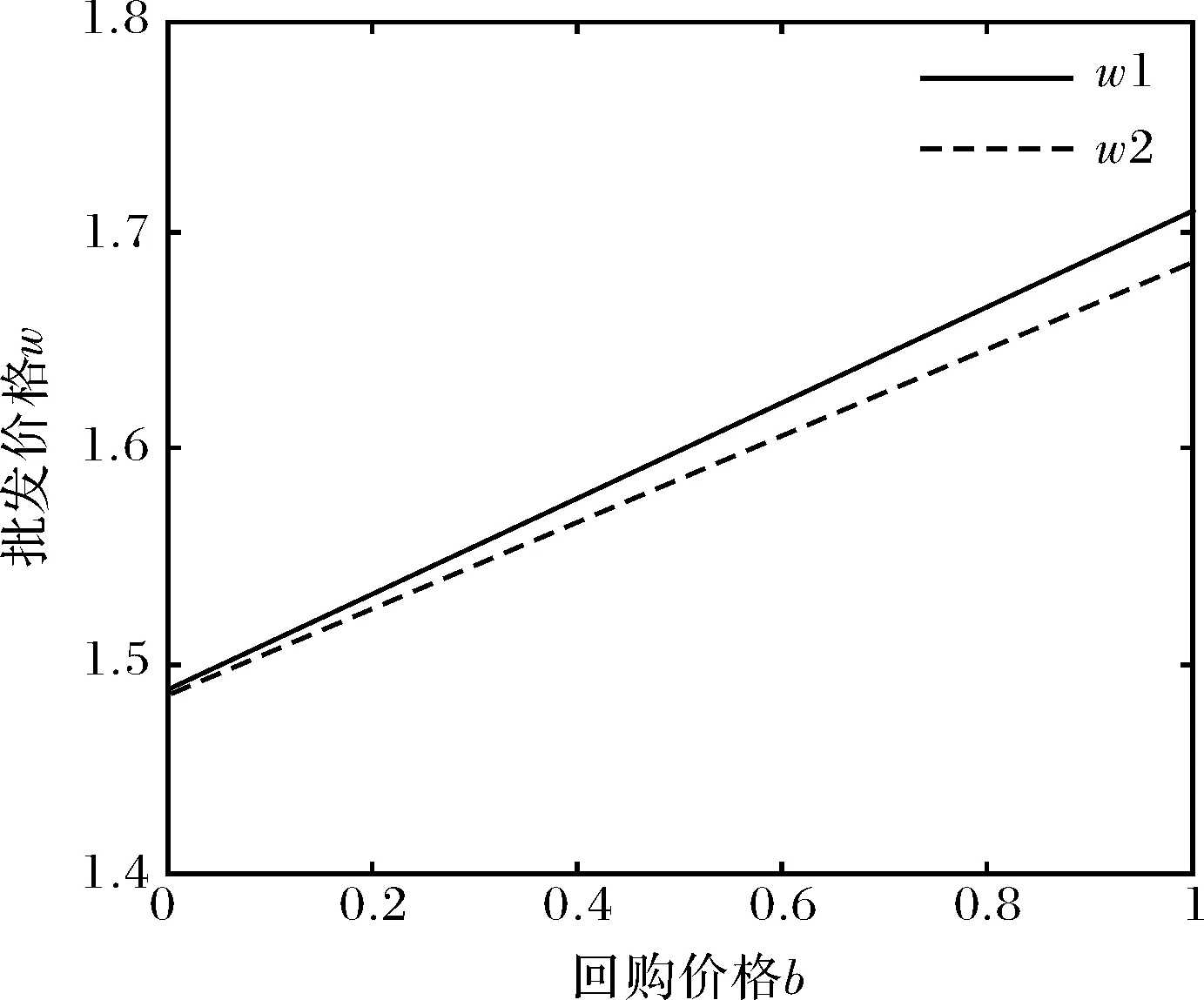
图10 回购价格对批发价格的影响Fig.10 The effect of buy-back price on wholesale price

5 结论

同时考虑生产商和零售商的风险偏好，基于η-CVaR准则研究了回购契约下供应链金融的融资与运营决策及其协调策略.研究发现，分散供应链的最优决策可以与集成供应链的最优决策实现协调，甚至出现超协调效应.生产商能够通过一定的回购契约改善供应链绩效.此外，零售商的风险规避特性会导致其最优订购量的减少，而生产商的风险偏好系数会对其最优批发价格决策产生重大影响.除了CVaR准则，衡量供应链绩效的准则还包括加权CVaR、效用函数等，不同准则下的决策与协调机制将是需要进一步研究的问题.

附录

命题1和推论1的证明：构造函数G(x)

(wq-k)(1+rf)

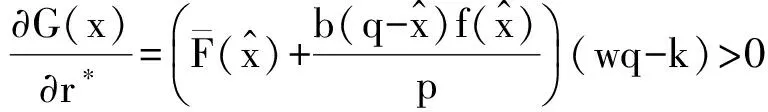
命题2和推论2的证明：对于(2)式，分两种情况进行最优解的讨论.

yr(q，vr)=vr-

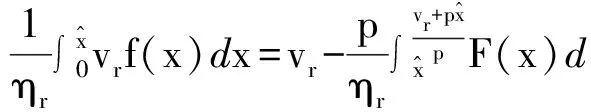
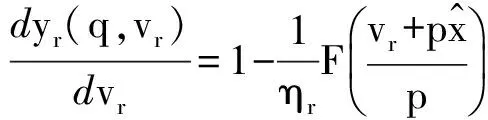
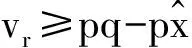
yr(q，vr)=vr-

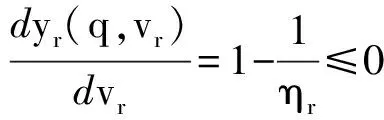
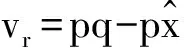
对q求一阶导数，

对q求二阶导数，

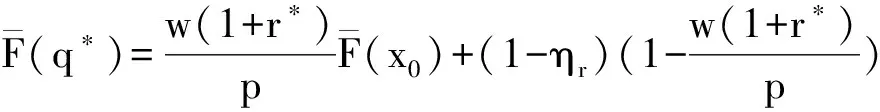
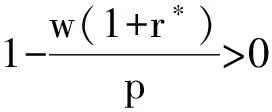
命题3的证明：对于(3)式，分3种情况进行最优解的讨论.

1)当vm≥(w-c)q时，

ym(q，vm)=vm-

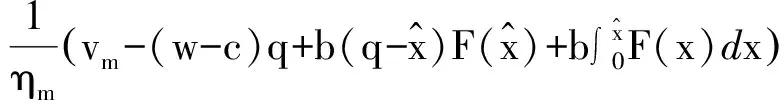
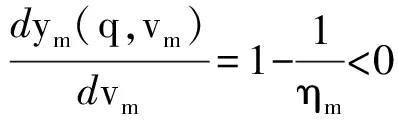
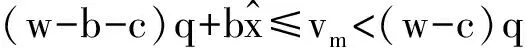
ym(q，vm)=vm-

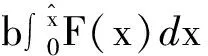
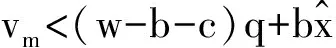
ym(q，vm)=vm-

对vm求一阶导数

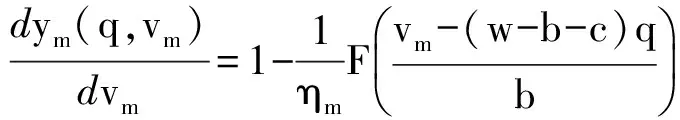
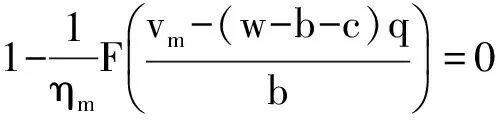
vm=bF-1(ηm)+(w-b-c)q.

CVaRm(πm)=(w-b-c)q+

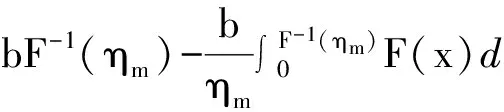
CVaRm(πm)=(w-c)q-

对w求一阶导数可得

命题4～6的证明：根据(4)式，分两种情况进行最优解的讨论.

1)当vs≥pqs+(w-c)qs-(wqs-k)(1+rf)时，

(wqs-k)(1+rf)-px)f(x)dx-

(wqs-k)(1+rf))f(x)dx=

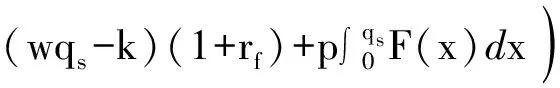
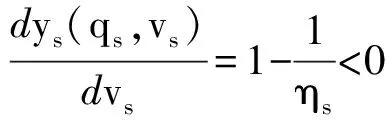
(2)当vs

ys(qs，vs)=vs-

(wqs-k)(1+rf)-px)f(x)dx=

令

得出

[1] SCHWEITZER M E，CACHON G P. Decision bias in the newsvendor problem with a known demand distribution: experimental evidence[J]. Management Science，2000，46(3): 404-420．

[2] QIN Y，WANG R，VAKHARIA A J，et al. The newsvendor problem: review and directions for future research[J]. European Journal of Operational Research，2011，213(2): 361-374．

[3] WU M，ZHU S X，TEUNTER R H. Newsvendor problem with random shortage cost under a risk criterion[J]. International Journal of Production Economics，2013，145(2):790-798．

[4] KATARIYA P A，CETINKAYA S，TEKIN E. On the comparison of risk-neutral and risk-adverse newsvendor problems[J]. Journal of the Operational Research Society，2014，65(7)：1090-1107．

[5] ZHANG Q H，DONG M，LUO J W，et al. Supply chain coordination with trade credit and quantity discount incorporating default risk[J]. International Journal of Production Economics，2014，153:352-360．

[6] DAI J S，MENG W D. A risk-averse newsvendor model under marketing-dependency and price-dependency[J]. International Journal of Production Economics，2015，160:220-229．

[7] XU M H，LI J B. Optimal decisions when balancing expected profit and conditional value-at-risk in newsvendor models[J]. Journal of Systems Science & Complexity，2010，23(6)： 1054-1070．

[8] 王新辉，汪贤裕.考虑销售商风险规避的双边信息不对称的供应链协调[J].中国管理科学，2015，23(3)：97-107．

[9] WEI Y，CHOI T M. Mean-variance analysis of supply chains under wholesale pricing and profit sharing schemes[J]. European Journal of Operational Research，2010，204(2)：255-262．

[10] CHIU C H，CHOI T M，Li X. Supply chian coordination with risk sensitive retailer under target sales rebate[J]. Automatica，2011，47(8)：1617-1625．

[11] CHEN X，SIM M，SIMCHI-LEVI D，et al. Risk adverse in inventory management[J]. Operations Research，2007，55(5)：828-842．

[12] 赵 霞，吴方卫，蔡 荣. 随机产出与需求下二级供应链协调合同研究[J].管理科学学报，2014，17(8)：34-47．

[13] 代建生，孟卫东. 基于CVaR的供应链联合促销的回购契约协调研究[J].中国管理科学，2015，22(7)：43-51．

[14] YAN N N，SUN B W. Coordinating loan strategies for supply chain financing with limited credit[J]. OR Sprctrum，2013，35(4)：1039-1058．

[15] CHEN X F. International Journal of A model of trade credit in a capital-constrained distribution channel Production economics [J]. 2015，159(C)：3477-357．

[16] AFELLAR R T，URYASEV S. Optimization of conditional value-at-risk[J]. Journal of Risk，2000，2(3)：21-42．

Coordination strategies for supply chain finance with buy-back contract under criterion ofη-CVaR

LIU Chongqing，YAN Nina

(Business School，Central University of Finance and Economics，Beijing 100081)

Under criterion of conditional value at risk (CVaR)，a supply chain finance (SCF) system comprising of a manufacture，a capital-constrained retailer and a bank are established. Considering the risk preference of both the manufacture and the retailer，the financing and operation decisions and coordination strategies of SCF with buy-back contract are studied，generating optimal decision of each side. Through investigation on the impacts of manufacture’s risk preference，retailer’s risk preference and buy-back price on the optimal decisions，the coordination strategies in SCF are analyzed. It is shown that the decentralized supply chain is able to coordinate with the centralized supply chain，and even super-coordination effects may appear. Finally，some numerical examples are conducted to verify the results．

supply chain finance; risk preference; CVaR; buy-back contract; coordination

2016-05-03.

国家自然科学基金项目(71372191)；中央财经大学2015年度研究生科研创新基金项目(201515).

1000-1190(2016)05-0704-09

F274

A

*E-mail: liuchongqing@139.com.