一个分数阶四翼混沌系统的动力学特性及其多元电路实现
2016-11-29杨志宏屈双惠马志春张彩霞
杨志宏,屈双惠,马志春,张彩霞
(石家庄学院 物理与电气信息工程学院,石家庄 050035)
一个分数阶四翼混沌系统的动力学特性及其多元电路实现
杨志宏*,屈双惠,马志春,张彩霞
(石家庄学院 物理与电气信息工程学院,石家庄 050035)
对一个分数阶四翼系统的相图、分岔图和Poincaré 截面等动力学特性进行了详尽的分析,利用Multisim电子工作平台设计了该系统的树型、链型以及树链混合型的多元模拟电路进行仿真,多元电路仿真结果均与Matlab数值模拟结果相一致,证实了所设计电路的有效性.
分数阶四翼系统; 动力学特性; 分岔图; Poincaré 截面; 多元模拟电路
随着信息化程度的不断提高,保障信息传输的安全性已逐步成为全球信息行业的焦点和难点问题,而如何进行更好的信息加密则是信息安全的核心问题. 非线性系统由于具有一些特有的复杂状态而在信息加密技术中越来越突显出它的优越性,也得到了越来越多的实际应用. 目前利用整数阶微积分非线性系统进行保密通信的研究已较为普遍,但对于分数阶微积分非线性系统而言,其理论研究还没有得以广泛的实践,发展相对滞后. 分数阶微积分与整数阶微积分的关系为,前者是后者的拓展,后者是前者的特例. 所以,分数阶微积分算子更具有普及性和代表性,更能够准确、真实地描述和反应现实系统的复杂本质. 同时,由于分数阶系统具有更大的密钥空间,相对整数阶系统而言拥有更高的实用价值. 因此,对分数阶混沌系统的实现电路开展深入研究有着广泛的意义[1-4].
本文设计出的分数阶混沌系统,它能够出现越过上、下吸引域界限的对角混沌吸引子,是一个具有四翼吸引子的系统. 在前期研究的基础上,我们发现本系统的信号具有相对较宽的频谱带宽,这更有益于在信息加密技术中实现其应用价值[5]. 本文同时对系统的庞加莱截面、分岔图等基本动力学特性进行了详细的研究,并设计了树型、链型等效阻容单元电路,通过独立使用或混合使用这两种单元电路去替换整数阶电路中的积分电容实现了对该分数阶系统的电路仿真,电路模拟与数值仿真结果完全一致,为今后将该系统应用于实践提供了强有力的依据.
1 分数阶微分的定义
分数阶微分虽然有多种不同的定义形式,但其科学性在实践中均已得到了证实. 本文选用目前使用较为广泛的一种分数阶微分定义—— RL分数阶微分,其形式为:
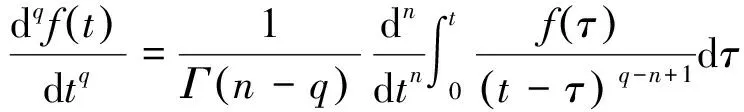
(1)
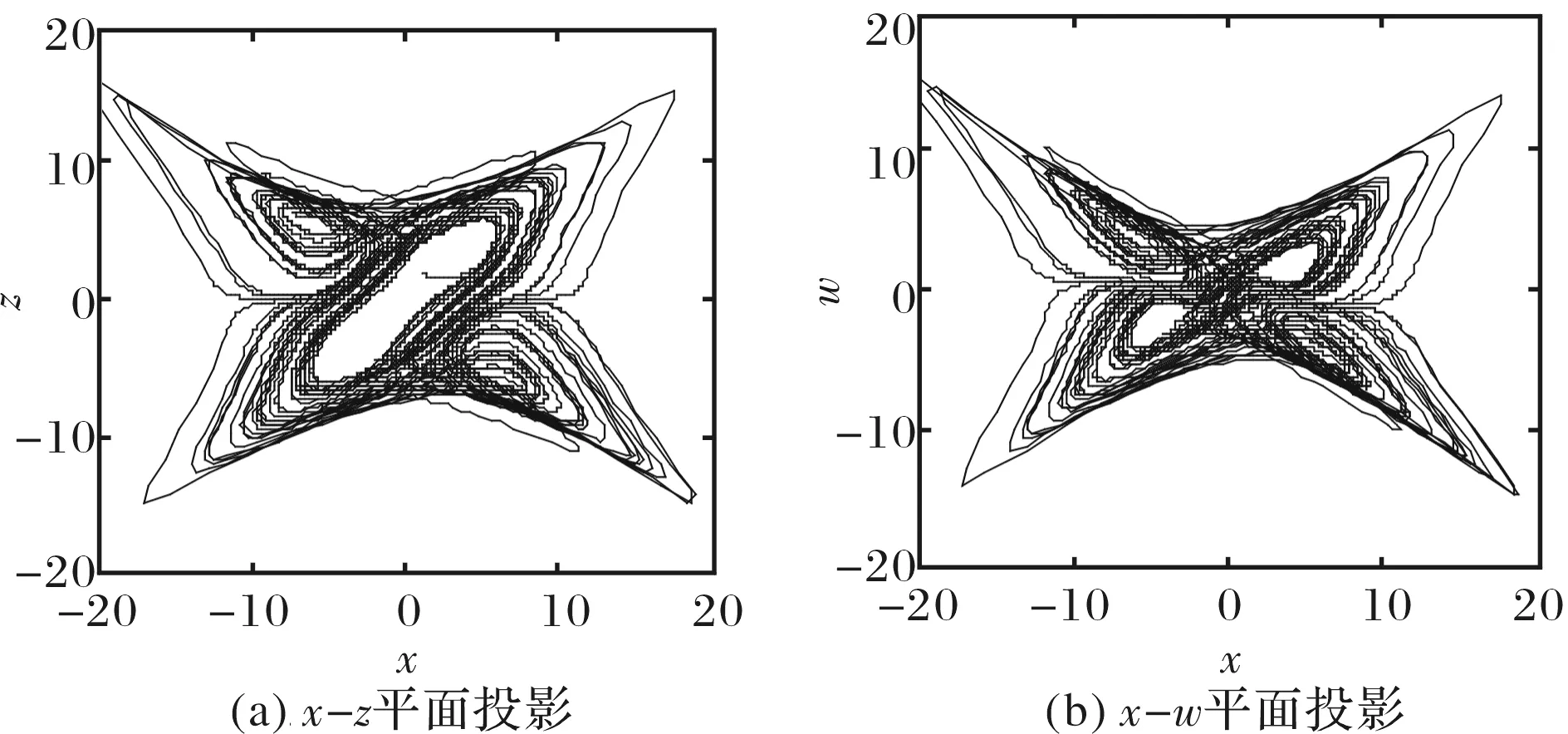
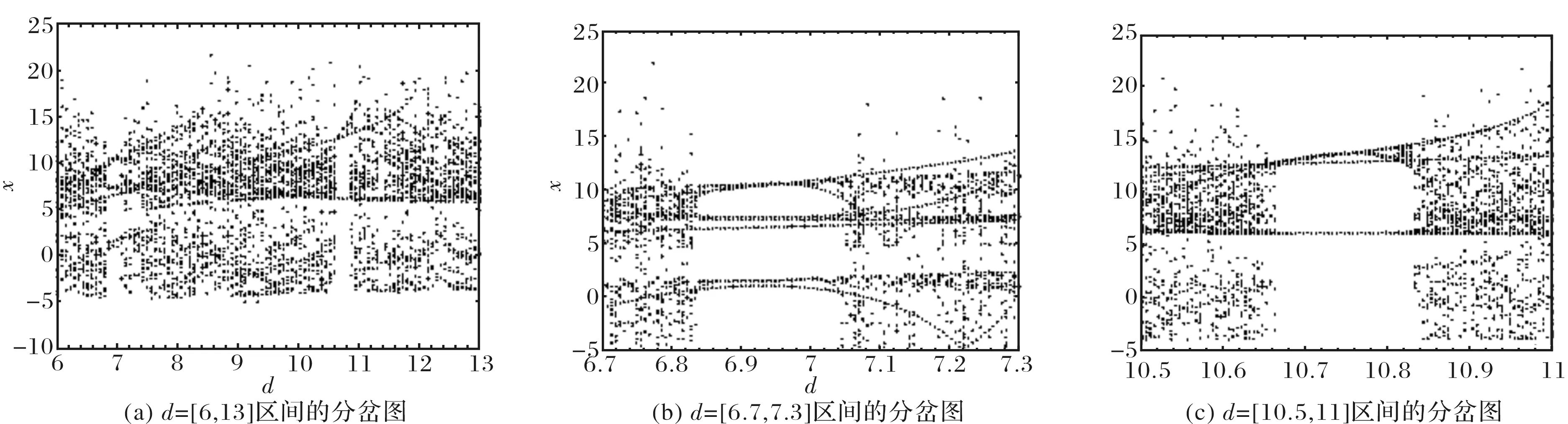
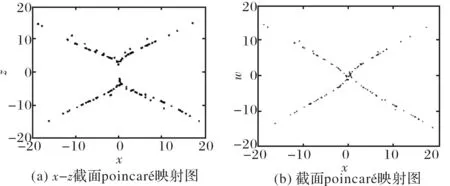
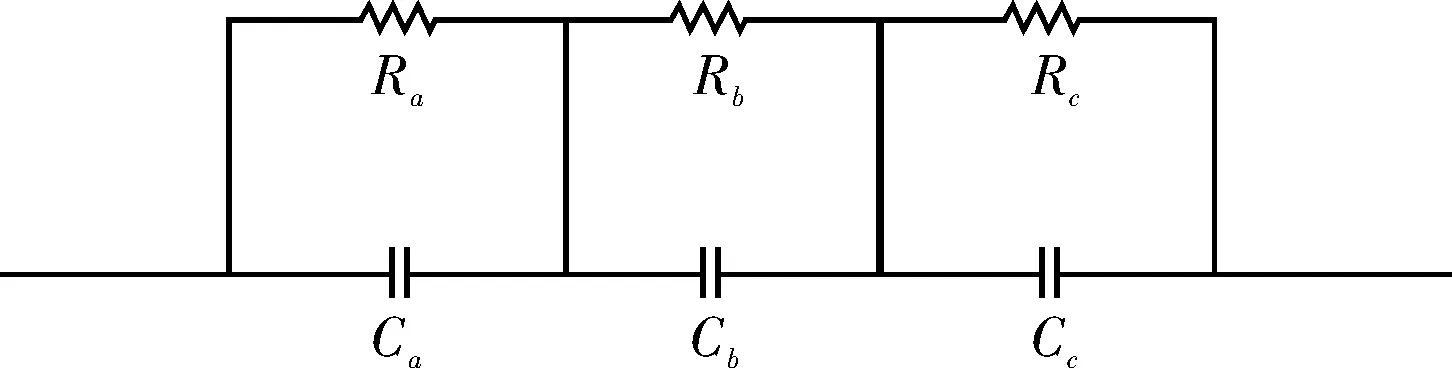
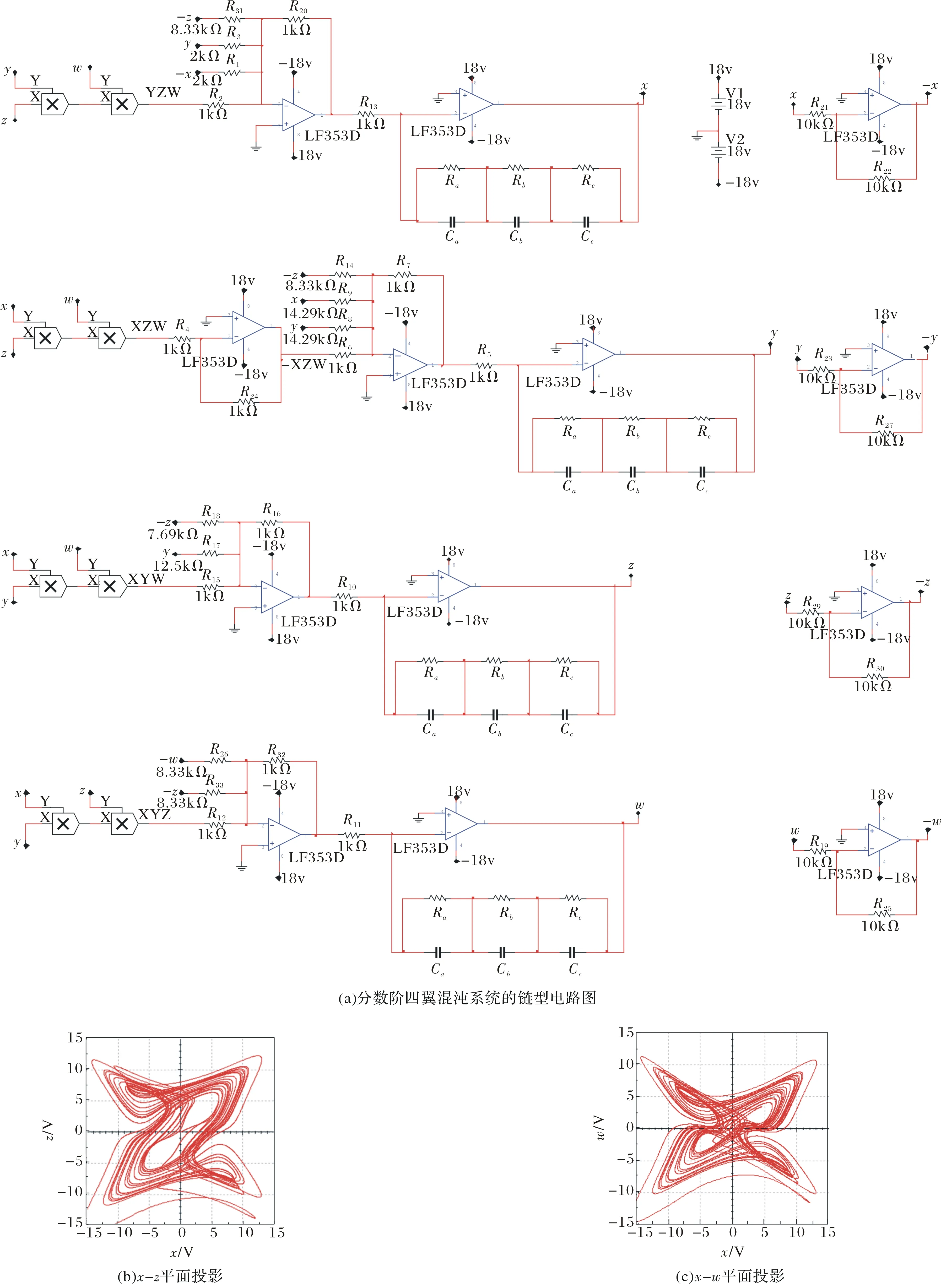
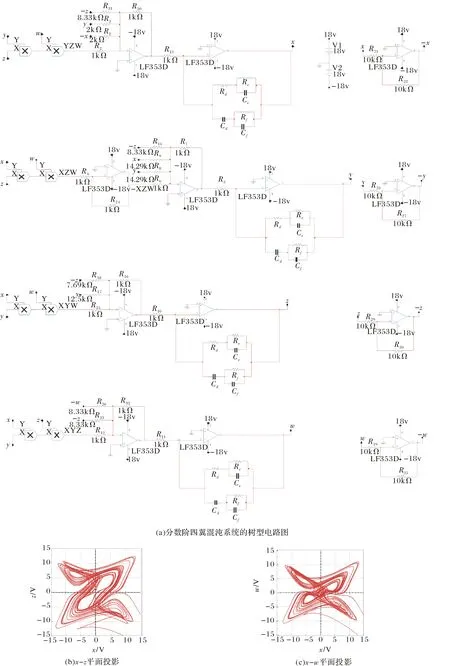
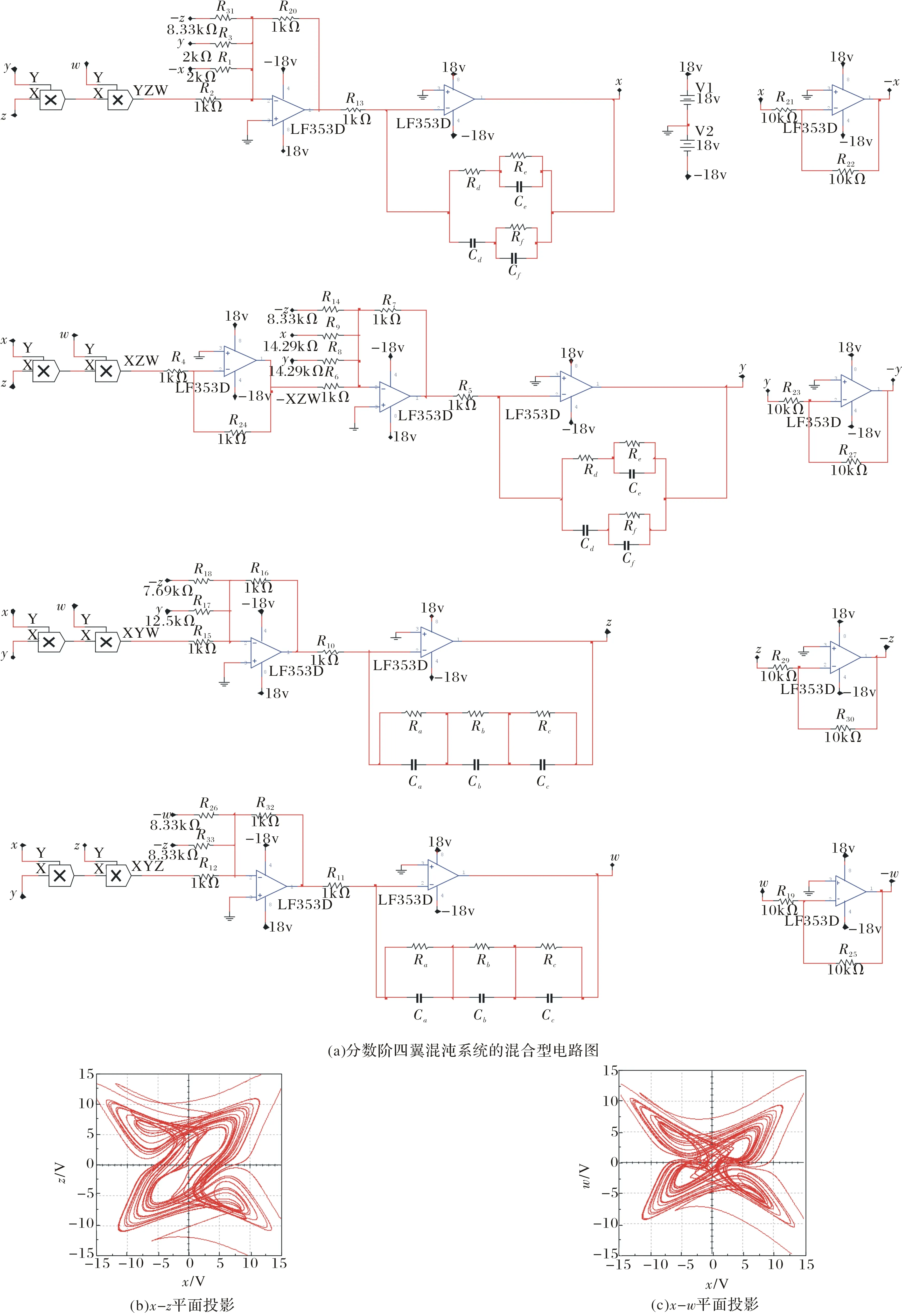
其中,Γ(·)为伽马函数,n-1 分数阶微积分的求解方法主要有两种:预估-校正法和时频域转换法,预估-校正法主要应用于数值求解,时频域转换法主要应用在工程上[6-8]. 本文对分数阶系统的数值仿真采用了预估-校正法,而电路仿真则采用了时频域转换法. 本文设计的分数阶四翼系统其数学形式为[9] (2) 采用预估-校正法对系统进行数值仿真,当取参数a=50,b=7,c=13,d=12,e=8,q=0.95时,可以得到该分数阶系统的吸引子相图如图1所示. 可以看到,系统的吸引子是一个能够越过上、下吸引域界限的对角混沌吸引子,是一个真正的四翼吸引子. 图2(a)给出了d=[6,13]时,变量 x 随参数d 变化时的分岔图,由图2(b)和图2(c)可以明显地观察到,在d=[6.83,7.04]以及d=[10.66,10.83]的区域内,系统出现周期窗口. 图1 分数阶四翼系统的相图Fig.1 Phase diagram of the four-winged fractional order system 图2 x 随 d 变化时的分岔图Fig.2 Birfurcation diagram of d vary with x 图3给出了参数a=50,b=7,c=13,d=12,e=8,q=0.95时系统(2)在y=0时的x-z 截面和x-w 截面的Poincaré映射图. 我们从上图中可以发现,Poincaré截面图上产生了多处成片的密集型点,这些叶片反复折叠并越过了上、下吸引域界限,表明了该系统确实能够产生越过上、下吸引域界限的真正四翼混沌吸引子. 图3 Poincaré截面图(y=0)Fig.3 Poincaré map(y=0) 采用时频域转换法进行电路仿真[6-8,10-11]. 假如时域函数f(t)的初始值是零,那么把(1)式进行拉普拉斯变换可表示如下: (3) 这里的分数阶微分算子“q”可以在频域中用传递函数H(s)=1/sq来实现. 通过求解复频域的传输函数1/sq,可推导出复频域的展开模式,再将复频域模式转化为时域的模式求解. 当q=0.95时,1/s0.95的1 dB误差的近似公式为[7]: (4) 对于分数阶电路,可通过利用等效阻容单元电路替换单个整数阶电路中的积分电容来实现. 以下分别给出了实现1/s0.95的树型、链型等效阻容单元电路,并通过独立使用或混合使用这两种单元电路实现了对该分数阶系统的多元电路模拟. 3.1 链型等效阻容单元电路 分数阶算子1/s0.95的链型等效阻容单元电路如图4所示,其传递函数可表示为 (5) 将(4)式、(5)式进行比较,可得到链型单元电路中的各电阻和电容值分别为Ra=15.1 kΩ,Rb=1.51 MΩ,Rc=692.9 MΩ,Ca=3.616 μF,Cb=4.602 μF,Cc=1.267 μF. 3.2 树型等效阻容单元电路 分数阶算子1/s0.95的树型等效阻容单元电路如图5所示,其传递函数可表示为 (6) 图4 链型等效阻容单元电路Fig.4 Chain type equivalent unit circuit 图5 树型等效阻容单元电路Fig.5 Tree type equivalent unit circuit 将(4)式、(6)式进行比较,可得到树型单元电路中的各电阻和电容值分别为 Rd=0.3258 MΩ,Re=694.1 MΩ,Rf=2.172 MΩ, Cd=1.049 μF,Ce=0.2135 μF,Cf=3.039 μF. 3.3 分数阶四翼系统的多元电路实现 图6(a)为在Multisim平台上设计的分数阶四翼混沌系统的链型仿真电路图,该电路共由4路模拟运算电路组成,每支电路中都采用了2个增益为0.1的模拟乘法器AD633实现对公式(2)中的三次非线性交叉乘积项的运算,运算放大器型号为LF353D,其电源电压为±18 V,链型等效阻容单元电路用以实现对各变量的分数阶积分运算. 对于每一路运算电路都可分别选用链型和树型2种单元电路实现对分数阶电路的运算,本文选用的分数阶四翼混沌系统是四维系统,共有24=16种组合方式,如表1所示. 表1 多元电路的组合方式 表1中的组合1,如图6(a)所示,通过独立使用链型单元电路实现了分数阶四翼系统的链型电路仿真,通过Multisim仿真可以在示波器上得到系统的吸引子相图,如图6(b)和图(c)所示. 若将图6(a)中的链型单元电路全部更换为树型单元电路,该组合方式对应于表1中的组合16,如图7(a)所示,可得到通过独立使用树型单元电路实现的该系统的树型电路仿真. 通过Multisim仿真可以在示波器上得到系统的吸引子相图,如图7(b)和图7(c)所示. 图6 分数阶四翼混沌系统的链型电路及仿真结果Fig.6 Chain type analog circuit and multisim experimental results of the four-winged fractional order system 图7 分数阶四翼混沌系统的树型电路及仿真结果Fig.7 Tree type analog circuit and multisim experimental results of the four-winged fractional order system 其余组合方式为树型和链型单元电路混合在一起时实现的分数阶四翼系统的混合电路.鉴于篇幅限制,本文只给出了该系统的组合13混合电路,如图8(a)所示,其中前两路电路选用了树形单元电路,后两路电路选用了链型单元电路,通过仿真得到系统的吸引子相图,如图8(b)和图8(c) 图8 分数阶四翼混沌系统的混合型电路及仿真结果(组合13)Fig.8 Mixed type plural analog circuit and multisim experimental results of the four-winged fractional order system 所示. 此外,对表1中 的其他13种混合电路也都进行了电路仿真实验,得到了相同的吸引子相图. 可以看出,以上3种组合电路得到的吸引子相图完全相同,均与matlab数值仿真得到的吸引子相图相一致. 对新提出的分数阶四翼混沌系统的动力学行为进行了分析,分数阶系统不仅能够更真实的反映出系统的混沌特性,而且比整数阶系统具有更大的密钥空间,所以分数阶系统在加密领域,如图像加密和信息加密等领域都具有更大的升值潜力. 设计了这个新分数阶系统的链型、树型、混合型多元模拟电路进行研究,各电路仿真均与数值仿真结果相一致,不仅验证了所设计电路的有效性和可靠性,也为实现该系统的实际应用奠定了基础. [1] LI C,CHEN G. Chaos and hyperchaos in the fractional order Rossler equations[J]. Physica A,2006,27(1): 685-688. [2] SUN K,WANG X,SPROTT J C. Bifurcations and chaos in fractional-order simplified Lorenz system[J]. International Journal of Bifurcation and Chaos,2010,20(4): 1209-1219. [3] 张成芬,高金峰,徐 磊. 分数阶Liu系统与分数阶统一系统中混沌现象及二者的异结构同步[J]. 物理学报,2007,56(9):5124-5130. [4] 王发强,刘崇新. Liu混沌系统的混沌分析及电路实验的研究[J]. 物理学报,2011,55(10):5061-5069. [5] 胡国四. 一类具有四翼吸引子的超混沌系统[J]. 物理学报,2009,58(6):3734-3741. [6] 孙克辉,杨静利,丘水生. 分数阶混沌系统的仿真方法研究[J]. 系统仿真学报,2011,23(11):2361-2370. [7] 黄丽莲,辛 方,王霖郁. 新分数阶混沌系统的异结构同步及其电路仿真[J]. 系统仿真学报,2012,24(7):1479-1484. [8] 闵富红,余 杨,葛曹君. 超混沌分数阶Lü系统电路实验与追踪控制[J]. 物理学报,2009,58(3): 1456-1461. [9] 杨志宏,屈双惠,王 清. 一个四翼超混沌系统的多翼效应及其控制电路实现[J]. 华中师范大学学报(自然科学版),2015,49(5): 696-700. [10] JIA H,CHEN Z,QI G. Topological horseshoe analysis and the circuit implementation for a four-wing chaotic attractor[J]. Nonlinear Dyn,2011,65:131-140. [11] 张若洵,杨世平. 分数阶共轭Chen混沌系统中的混沌及其电路实验仿真[J]. 物理学报,2009,58(5):2957-2962. The dynamic properties of a four-winged fractional order chaotic system and its plural circuit implementation YANG Zhihong,QU Shuanghui,MA Zhichun,ZHANG Caixia (Department of Physics and Electrical Information Engineering,Shijiazhuang University,Shijiazhuang 050035) Some basic dynamic properties of a four-winged fractional order system are investigated,such as phase diagrams,bifurcation diagrams and Poincaré sections. Using Multisim electronics platform,tree type,chain type and mixed type plural analog circuit are designed to implement the new system. The plural circuit simulation results are consistent with the Matlab emulation results,which show the effectiveness of the proposed circuit. four-winged fractional order system; dynamic properties; bifurcation diagrams; Poincaré sections; plural analog circuit 2016-05-24. 河北省自然科学基金项目(F2013106079); 石家庄市科技计划指导项目(141131561); 石家庄学院科研平台建设成果(XJPT002). 1000-1190(2016)05-0665-07 O415 A *E-mail: yangzhihon_g@126.com.2 分数阶四翼系统的模型及其动力学行为研究
3 分数阶四翼系统的电路设计
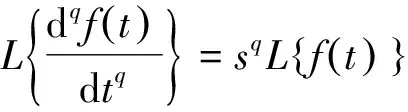
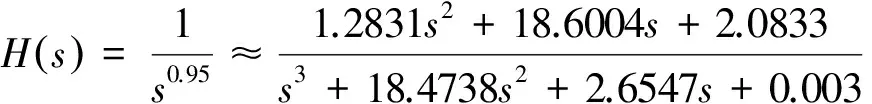
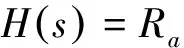
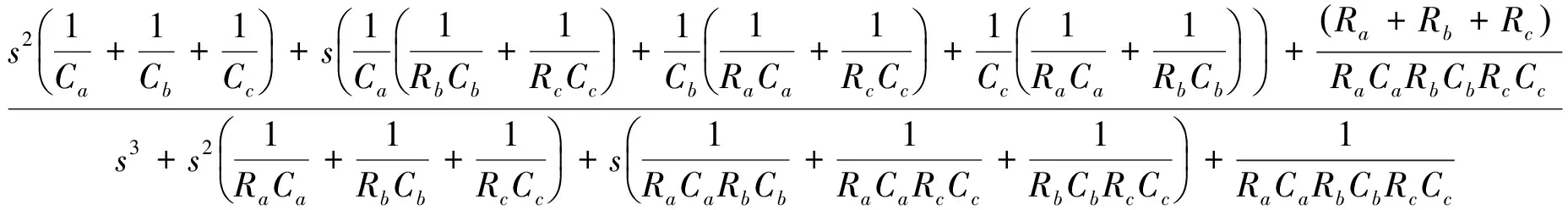
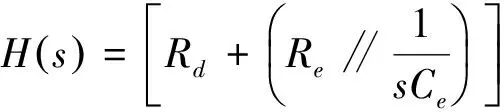
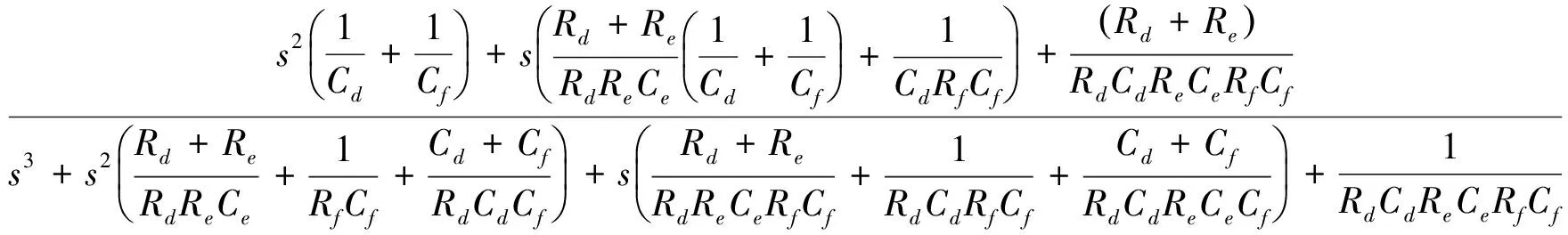


4 结论
