次大体积增长的流形的曲率与拓扑研究

薛 琼，陈欢欢，陈爱云，肖小峰

(1.武汉理工大学 理学院，武汉 430070； 2.武汉纺织大学 机械工程与自动化学院，武汉 430073)



次大体积增长的流形的曲率与拓扑研究

薛 琼1*，陈欢欢1，陈爱云1，肖小峰2

(1.武汉理工大学 理学院，武汉 430070； 2.武汉纺织大学 机械工程与自动化学院，武汉 430073)

该文研究了一类具有非负Ricci曲率和α(α∈[0，2])次衰减截曲率下界的完备非紧黎曼流形.利用Toponogov型比较定理和临界点理论，证明了该流形在一定次大体积增长条件下具有有限拓扑型，从而推广了J.Sha、Z.Shen和C.Xia的关于这类流形的一系列结果.

Ricci曲率； 次大体积增长； Excess函数； Busemann函数

由著名的Cheeger-Gromoll核心定理[1]知，具有非负截曲率完备非紧的黎曼流形具有有限拓扑型.但是，如果没有其他限制条件，光有非负Ricci曲率的条件是不能得到这一个结论的.对此，Sha和Yang在[2]中构造出了相应的反例.熟知，非负Ricci曲率完备非紧的n维黎曼流形具有如下的体积增长估计：

c(n)vol[B(p，1)]r≤vol[B(p，r)]≤ωnrn，

其中，c(n)是一常数，ωn是Rn中单位球的体积.于是可以

定义1[3]设M是具非负Ricci曲率完备非紧的黎曼流形，若

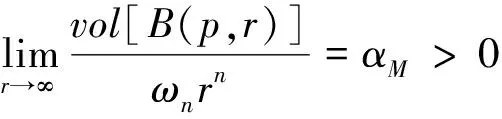
则称M具有大体积增长.

定义2 设M是具非负Ricci曲率完备非紧的黎曼流形，若

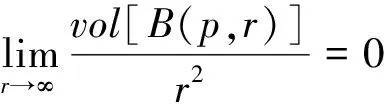
则称M具有小体积增长．

Bishop-Gromov体积比较定理[4]的一个重要应用是研究具有非负Ricci曲率和二次衰减截曲率下界的非紧Riemann流形在一定体积增长条件下的有限拓扑型问题．

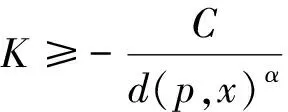
当α=2时，称M在基点p处具有系数为C的二次衰减截曲率下界．

1 预备知识及引理

在引出结论之前，先给出一些记号．

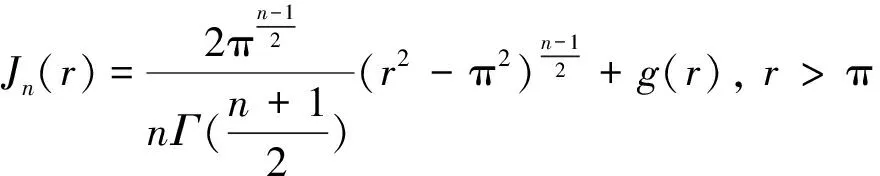
(1)

(2)

其中

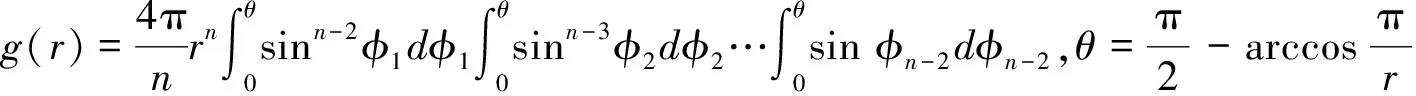
(3)

令In(r)rn-1=Jn(r)，那么当r>π，In(r)是关于r单调递减函数．

本文研究一类完备非紧n维Riemann流形满足RicM≥0，

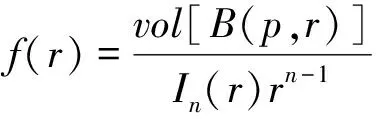
(4)

(5)

其中，R是一给定的大的常数．

注 这里M满足(4)、(5)是既非大体积增长又非小体积增长，称M具有次大体积增长．

记∑为p点处切空间TpM上单位球SpM的一个闭子集.令

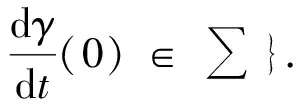
∑p(r)={v∈SpM|γ(t)=expp(tv)∶[0，r)→M是一条极小测地线}．

注意

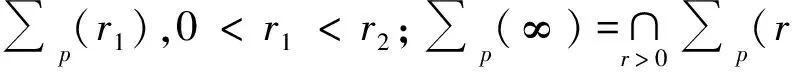
引理1[10]设(M，g)是具有非负Ricci曲率的完备非紧n维Riemann流形，且满足(4)-(5)，则对任意的x∈∂B(p，r)和足够大的r，有

h∶=d(x，B∑p(2r)(p，2r))≤

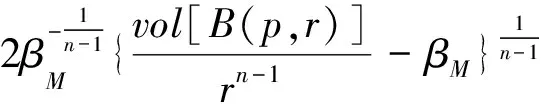
(6)

为了证明定理，还需如下定义和引理.首先给出截曲率的Toponogov型比较定理，这是临界点理论的基础．

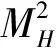
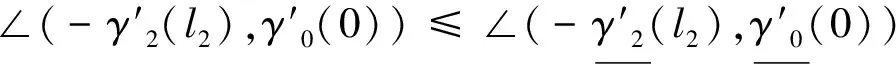
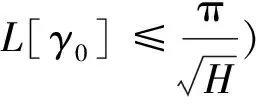
定义5 对任意p，q∈M，p，q的Excess函数定义为

epq(x)=d(x，p)+d(x，q)-d(p，q)，

其中d(p，q)表示从p到q的距离．

结合以上定义及关于边的Ricci曲率的Toponogov型比较定理[12]，Z.Shen在[13]中得到了推广的Excess估计，给出了一个上界．

若对任意的(k+1)维子空间V⊂TpM中的一组标准正交基{ei，…，ek+1}，曲率张量R(x，y)z满足

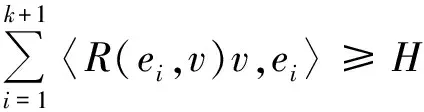
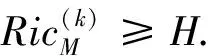
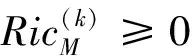
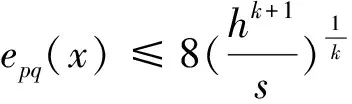
(7)

这里h=d(x，γ)，s=min(d(p，x)，d(q，x))．

定义6 对任意r>0，记S(p，r)为以p为中心以r为半径的测地球面.定义Bp∶M→M为

Bp(x)∶=d(x，S(p，2r(x)))-r(x)，

其中，r(x)∶=d(p，x).这是典型的Busemann函数．

J.Sha和Z.Shen在[7]中证明了

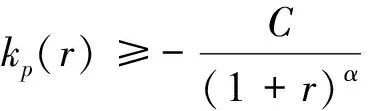
那么M具有有限拓扑型．

2 主要结果及其证明

利用Busemann函数与Excess函数的关系，可以证明如下结论，

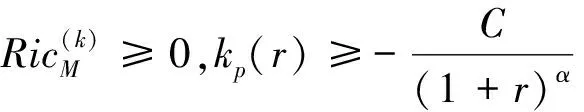
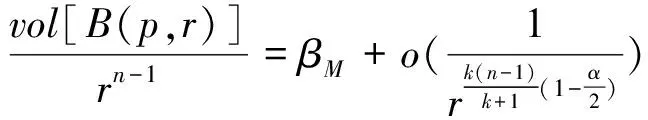
(8)

那么M具有有限拓扑型．

证明 对任意的x∈M，记r(x)=d(p，x).设γ:[0，2r(x)]→M是从点p到点q=γ(2r(x))的一条极小测地线，使得

h∶=d(x，γ)=d(x，B∑p(2r(x))(p，2r(x))).

根据引理1中的(6)，可知当r(x)>R时，

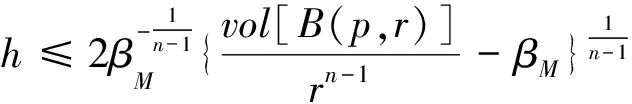
(9)

注意min(d(p，x)，d(q，x))≥r(x)．

再通过引理3中的(7)和(9)及Bp(x)的定义，可得

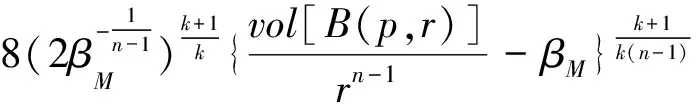
那么

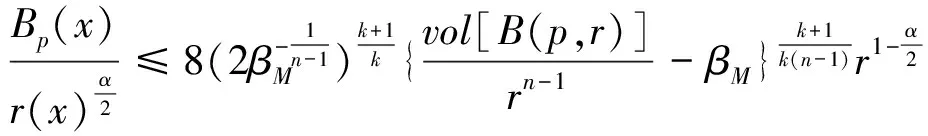
应用Toponogov型比较定理和距离函数的临界点理论又可证明：

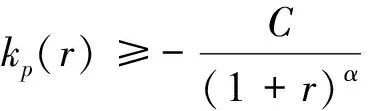
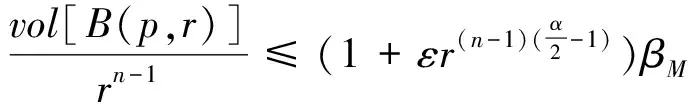
(10)

那么M具有有限拓扑型．

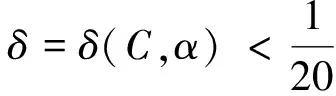
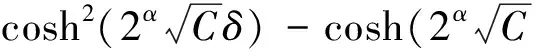
(11)

对任意的x∈M，记r=d(p，x)>R.只需证明x点不是p点的临界点即可.设γ:[0，2r]→M是从点p到点q=γ(2r)的一条极小测地线，使得

h∶=d(x，γ)=d(x，B∑p(2r)(p，2r)).

由引理1中的(6)，条件(10)及ε的选取，可知当r>R时，

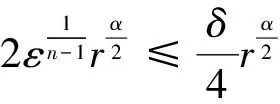
(12)

作一条从x到q的极小测地线σ.对任意的从x到p的极小测地线σ1，取

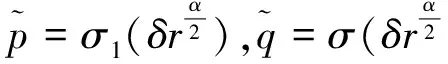
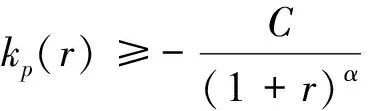
(13)

这里θ=∠(σ′(0)，σ′1(0))．

另一方面，取m∈γ使得d(x，m)=d(x，γ)，那么由三角不等式及(12)可得

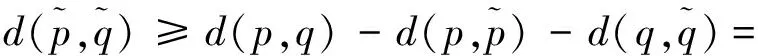
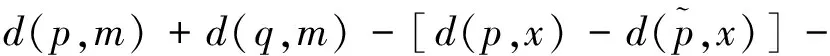
[d(p，m)-d(p，x)]+[d(q，m)-d(q，x)]≥

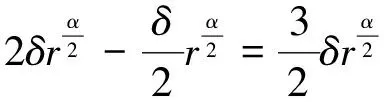
(14)

把(14)带入(13)，并结合(11)，得到

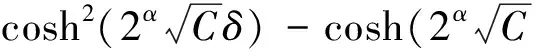
因此，x点不是p点的临界点，故M具有有限拓扑型．

注 定理2中条件(10)包含了定理1中条件(8)，从而推广了定理1.以上所得结果均推广了J.Sha、Z.Shen和C.Xia的关于这类流形的一系列结果．

[1] CHEEGER J，GROMOLL D. On the structure of complete manifolds of nonnegative Ricci curvature[J]. Ann of Math，1972，96:413-443．

[2] SHA J，YANG D. G. Examples of manifolds of positive Ricci curvature[J]. J Differential Geom，1989，29∶95-103．

[3] GROMOY M. Metric structures for Riemannian and non-Riemannian spaces[M]. Boston: Birkhäuser Boston Inc，1999．

[4] BISHOP R.L，CRITTENDEN R J. Geometry of manifolds[M]. New York: Academic Press，1964．

[5] ABRESCH U. Lower curvature bounds，Toponogov’s Theorem，and bounded topology[J]. I Ann Sci Ecole Norm Sup，1985，18:651-670．

[6] ABRESCH U. Lower curvature bounds，Toponogov’s Theorem，and bounded topology，II[J]. Ann Sci Ecole Norm Sup，1987，20:475-502．

[7] SHA J，SHEN Z. Complete manifolds with nonnegative Ricci curvature and quadratically nonnegatively curved infinity[J]. Amer J Math，1997，119:1399-1404．

[8] XIA C. Open manifolds with nonnegative Ricci curvature and large volume growth[J]. Comment Math Helv，1999，74: 456-466．

[9] XIA C. Large volume growth and the topology of open manifolds[J]. Math Zeit，2002，239:515-526．

[10] XUE Q，XIAO X. Complete manifolds with nonnegative Ricci curvature and sub-large volume growth[J].J of Math，2012，32(4): 629-636．

[11] MACHIGASHIRA Y. Complete open manifolds of nonnegative radial curvature[J].Pacific J Math，1994，165: 153-160．

[12] DAI X，WEI G. A comparison-estimate of Toponogov type for Ricci curvature[J]. Math Ann，1995，303: 297-306．

[13] SHEN Z. On complete manifolds of nonnegative kth-Ricci curvature[J].Tran Amer Math Soc，1993，338: 289-310．

Research on the curvature and the topology of manifolds with sub-large volwume growth

XUE Qiong1，CHEN Huanhuan1，CHEN Aiyun1，XIAO Xiaofeng2

(1.School of Science，Wuhan University of Technology，Wuhan 430070;2.School of Mechanical Engineering and Automation，Wuhan Textile University，Wuhan 430073)

In this paper，complete noncompact Riemannian manifolds are studied with nonnegative Ricci curvature and lower bound of α(α∈[0，2])-sectional curvature decay. By Toponogov’s comparison theorems and critical point theory，the above manifold is demonstrated to have finite topological type with certain sub-large volume growth，which extend these results presented by J.Sha，Z.Shen and C.Xia．

Ricci curvature； sub-large volume growth； excess function； Busemann function

2016-05-10.

国家自然科学基金项目(61573012); 中央高校基本科研业务费专项资金项目(2015IA010)．

1000-1190(2016)05-0652-04

53C20

A

*E-mail: rabbit_801005@163.com.