剪切集的上盒维数的一种等价刻画

殷峰丽，王 聪

(1.周口师范学院 数学与统计学院，河南 周口 466001; 2.华中师范大学 数学与统计学学院，武汉 430079)



剪切集的上盒维数的一种等价刻画

殷峰丽1，王 聪2*

(1.周口师范学院 数学与统计学院，河南 周口 466001; 2.华中师范大学 数学与统计学学院，武汉 430079)

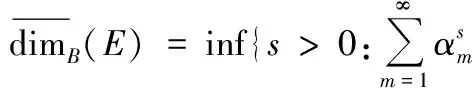
剪切集； 上盒维数； 间隔序列

上盒维数是分形几何中非常重要的概念，也有着十分广泛的应用.本文着重考虑剪切集这一类分形集的上盒维数. Falconer在文[1]给出一维剪切集E的上盒维数和间隔序列的关系，即

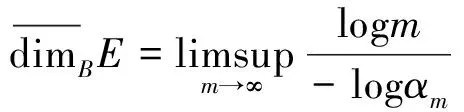
其中{αi}i≥1是集合E的间隔序列.饶辉等人在文[2]给出满足一定条件，上述结果可以推广到高维.本文在此基础上给出了剪切集上盒维数的另一种刻画：

应用此刻画，证明了文献[3-5]中的关于齐次Cantor集上盒维数的一个主要结论.该结论对齐次Cantor集填充维数的计算起着关键性的作用．

1 预备知识

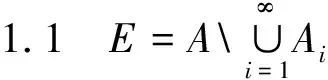
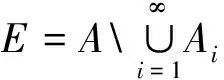
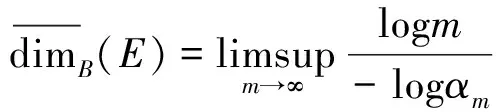
2 主要结论及证明

证明 首先，证明

成立．

(记n0=1)．

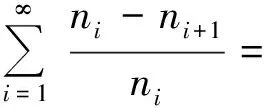
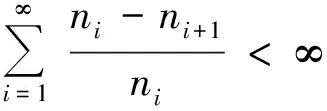
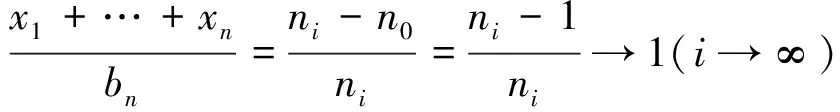
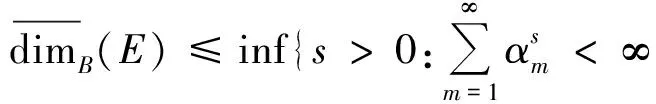
其次，证明

成立．

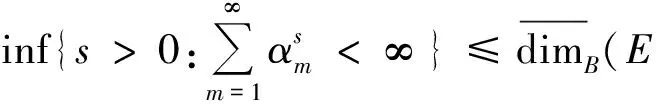
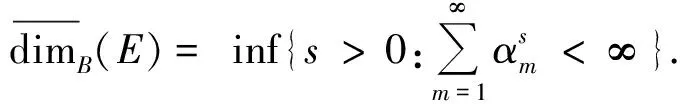
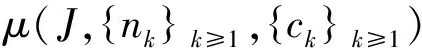
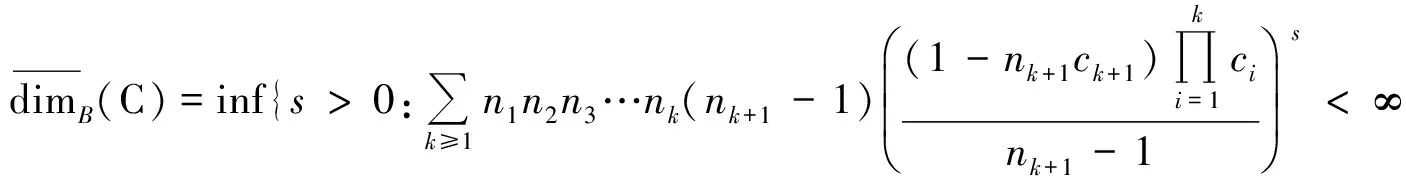
证明 由于

和定理1.3可得

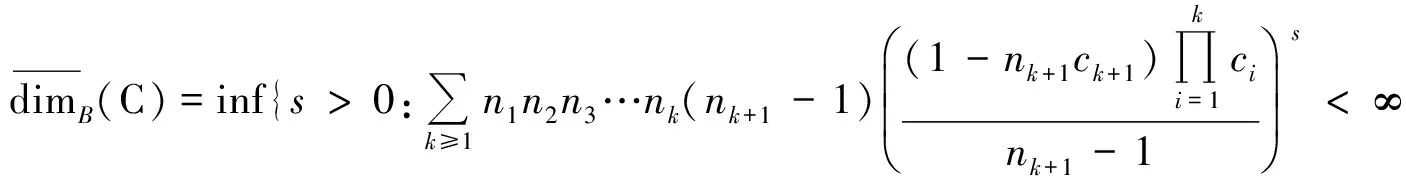
定理3.1[2]设E是d的紧集.如果存在一个常数C和一个趋向于0的序列k≥1且满足=1，以及E(δk)的每一个连通分支的勒贝格测度都小于，则

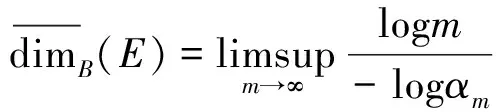
由定理2.2可得

[1] FALCONER K. Techniques in Fractal Geometry[M].Chichester，1997．

[2] RAO H，RUAN H J，YANG Y M. Gap sequence，Lipschitz equivalence and box dimension of fractal sets[J].Nonlinearity，2008，21(6):1339-1347．

[3] TRICOT C.Douze definitions de la densite logarithmique[J].C R Acad Sc Paris，1981，293:549-552．

[4] 文志英. 分形几何的数学基础[M].上海：上海科学技术教育出版社，1999．

[5] 丰德军，文志英，吴 军. 齐次Moran集的维数[J].中国科学(A)，1997，27(1):1-7.

[6] G B，ICD. On Kronecker’s lemma[J]. Gaz Mat，1980(2):57-59．

[7] BESICOVITCH A S ，TAYLOR S J. On the complementary intervals of a linear closed set of zero Lebesgue measure[J].Lond Math Soc，1945，29:49-59．

[8] FALCONER K.Fractal Geometry[M].Mathematical Foundation and Applications. Chichester: John Wiley & Sons，1990．

An equivalent definition of the upper box dimension of cut-out sets

YIN Fengli1，WANG Cong2

(1.School of Mathematics and Statistics，Zhoukou Normal University，Zhoukou，Henan 466001;2.School of Mathematics and Statistics，Central China Normal University，Wuhan 430079)

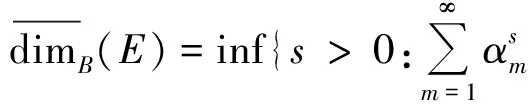
cut-out set; upper box dimension; gap sequence

2016-07-06.

国家自然科学基金面上项目(11271148).

1000-1190(2016)05-0649-03

O192

A

*通讯联系人. E-mail: 240765489@qq.com.