某类与In算子有关的解析函数的不等式

郭 栋，李宗涛

(1.滁州职业技术学院 基础部，安徽 滁州 239000； 2.广州民航职业技术学院 数学教学部，广州 510403)



郭 栋1，李宗涛2

(1.滁州职业技术学院 基础部，安徽 滁州 239000； 2.广州民航职业技术学院 数学教学部，广州 510403)

令H表示在U={z:|z|<1}内形如

f(z)=z+a2z2+a3z3+…

(1)

的解析函数f(z)的全体所成的函数类．

对于复数(或实数)a，b，c(c≠0，-1，-2，…)，定义超几何级数为

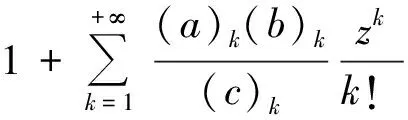
其中

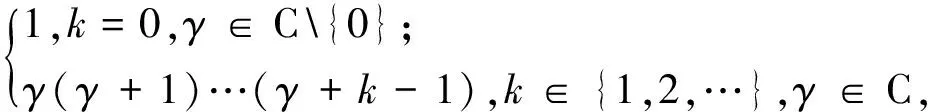
此级数在U内绝对收敛解析．

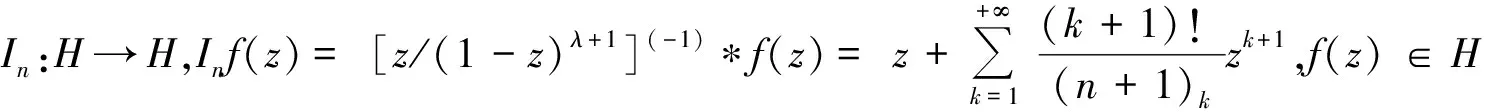
定理A 设f(z)∈S，f(z)由(1)式给出，0≤μ<1，则

且对每个μ等号都成立．

文献[2]中定义函数类P(α)={f(z)∈H，Re f′(z)>α，0≤α<1;z∈U}，文献[3]中定义了函数类:

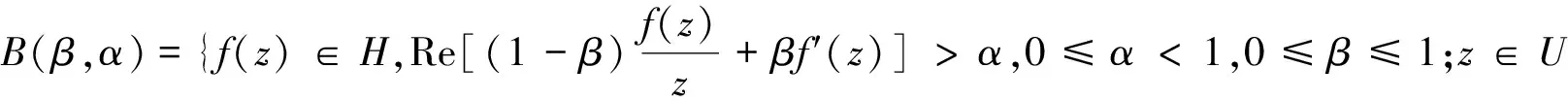
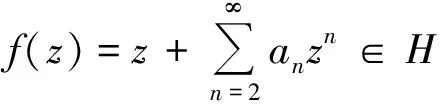
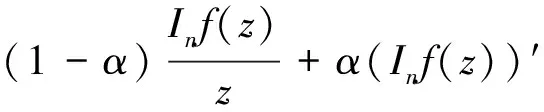
(2)

则记函数f(z)∈H(a，n;A，B)．

当参数α，B，A取特殊值时，可得一些特殊的解析函数类.例如:

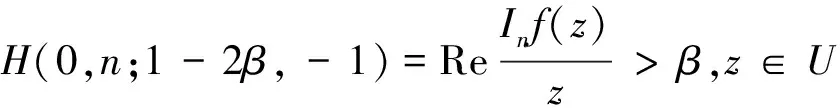
H(0，0;1，-1)=H(1，1;1，-1)=

Re f′(z)>0，z∈U;

H(1，n;1，-1)=Re(Inf(z))′>0，z∈U；

H(1，0;1，-1)=Re[f′(z)+zf″(z)]>0，z∈U

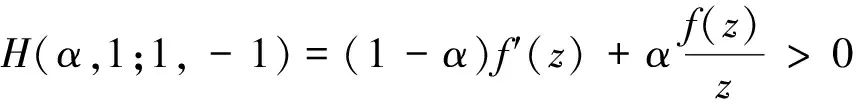
z∈U．

近年来，许多作者[4-6]研究了与NOOR算子相关的各种解析函数类和亚纯函数类．

1 引理

为了导出主要结果，需要如下引理．

引理1[10]设ω(z)=d1z+d2z2+…在z∈U时解析，且|ω(z)|≤|z|，则

|d1|≤1，|d2|≤1-|d1|2．

引理2[11]设p(z)=1+p1z+p2z2+…在U={z:|z|<1}内解析且满足Re p(z)>0，则

2 主要结果及证明

定理1 假设f(z)∈H，由式(1)给出，f(z)∈H(α，n;A，B)，α≠1，u为复数，则

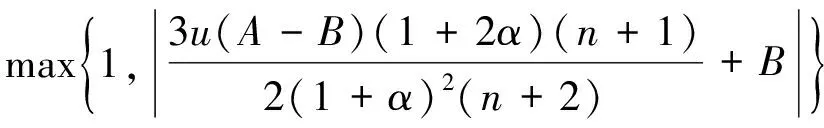
证明 因为f(z)∈H(α，n;A，B)，所以存在ω(z)=1+d1z+d2z2+…，使得

(3)

将Inf(z)的幂级数展开式代入(3)式，并比较恒等式两边的z和z2两项的系数，可得

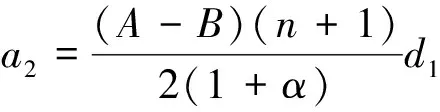
由引理1可得:

H(x)=C+CDx2，

E=2B(1+α)2(n+2)+3u(A-B)(1+2α)(n+1).则

相应地极值函数为：

|a2|≤(n+1)，

和

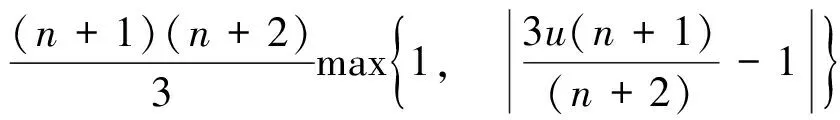
且对所有的u等号都成立．

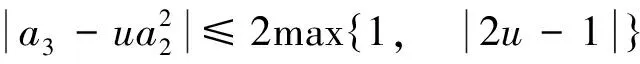
且对所有的u等号都成立．

推论3 假设Re f′(z)>0，z∈U，由式(1)给出，u为复数，则有|a2|≤1，和

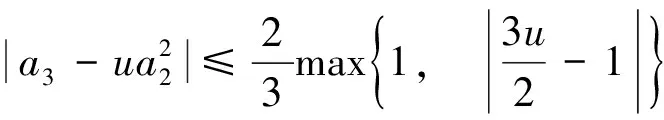
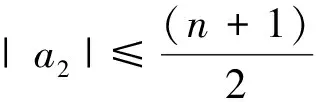
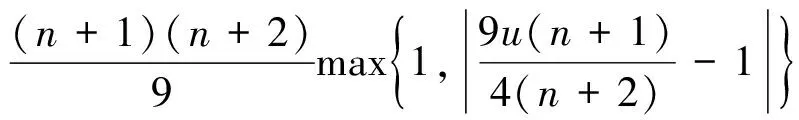
且对所有的u等号都成立．

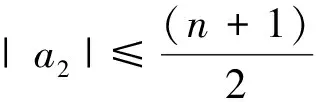
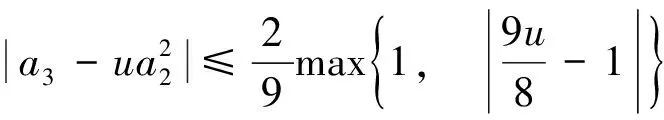
且对所有的u等号都成立．

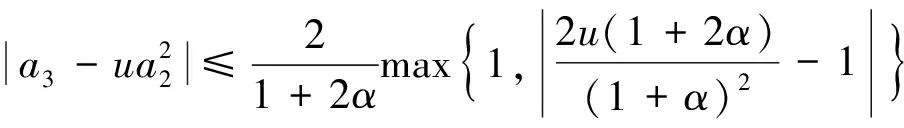
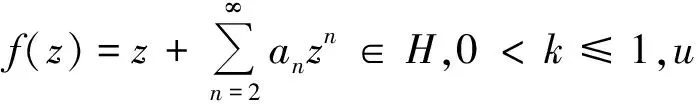
且对所有的u等号都能成立．

证明 定理的假设条件等价于存在一个p(z)∈P满足下列式子

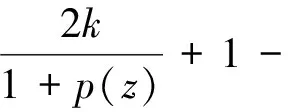
(4)

将Inf(z)，p(z)的幂级数展开式代入(4)式，并比较恒等式两边的z和z2两项的系数，可得

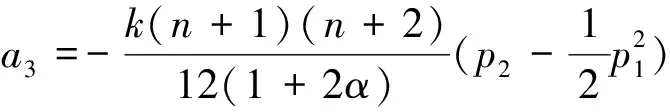
由式(4)及引理2可得:

所以相应的极值函数为:

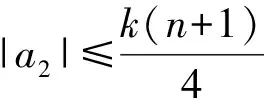
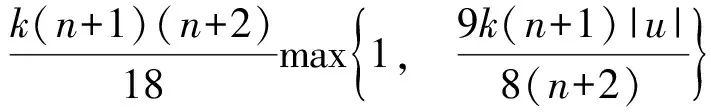
且对所有的u等号都能成立．

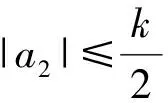
且对所有的u等号都能成立．

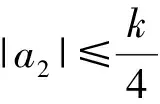
且对所有的u等号都能成立．

[2] Owa S，Aouf M K，Nasr M A.Note on subclass of close-to-convex functions of order α[J]. Internat. J Math Sci，1990，13(1):189-192．

[4] 魏 丽，刘名生. 涉及Noor多重积分算子的解析函数的中间定理[J].华南师范大学学报(自然科学版)，2010，2(1):9-13．

[5] 施冬芳，鲁大前，王 敏. 由NOOR积分算子定义的解析函数的性质[J].扬州大学学报(自然科学版)，2008，1(11):1-4．

[6] 刘文娟，彭 娟，杨 清. 与NOOR积分算子有关的多叶解析函数子类的性质[J].扬州大学学报(自然科学版)，2012，3(15):8-11．

[10] 夏道行，张开明. 从属函数的一些不等式[J]. 数学学报，1958，8(3):408-412．

GUO Dong1，LI Zongtao2

(1.Foundations Department，Chuzhou Vocational and Technical College，Chuzhou，Anhui 239000;2.Department of Mathematics Teaching，Guangzhou Civil Aviation college，Guangzhou 510403)

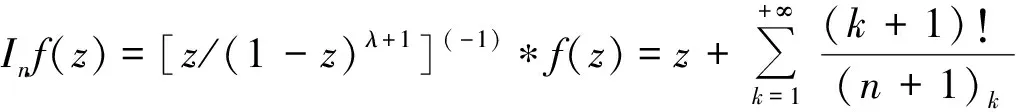
2016-05-08.

安徽省高校自然科学基金资助项目(KJ2015A372)；广东省博士启动项目(2016A030310106).

1000-1190(2016)05-0645-04

O174.51

A

*通讯联系人. E-mail: gd791217@163.com.