双极能量输运稳态模型弱解的存在性
2016-11-29董建伟朱军辉王艳萍
董建伟,朱军辉,王艳萍
(郑州航空工业管理学院 理学院,郑州 450015)
双极能量输运稳态模型弱解的存在性
董建伟*,朱军辉,王艳萍
(郑州航空工业管理学院 理学院,郑州 450015)
考虑一个半导体双极能量输运稳态模型,在Dirichlet-Neumann混合边界条件下,利用截断方法和Leray-Schauder不动点定理得到了其模型弱解的存在性. 研究结果表明,如果电子密度、空穴密度和粒子温度在Dirichlet边界处有正的上、下界,则它们在区域内部也有正的上、下界.
能量输运模型; 稳态解; 存在性
1 引言和主要结果
描述亚微半导体器件中载流子运动规律的宏观模型常见的有漂移-扩散模型、能量输运模型和流体动力学模型. 由于漂移-扩散模型未考虑热电子效应,在半导体器件的模拟中会给出不准确的结果,而完整的流体动力学模型形式过于复杂,不便于进行数值模拟,于是人们开始转向研究能量输运模型[1-7]. 最近,Jungel等人[8]从流体动力学方程组中推导出了一个简化的能量输运模型:
nt-div((nθ)+nV)=0,
(1)
div(nθ)=n(θ-θL(x)),
(2)
-ΔV=n-C(x),x∈Ω,t>0,
(3)
其中电子密度n、电子温度θ和电位势V为未知函数;晶格温度θL(x)和杂质密度C(x)为已知函数,Ω⊂Rd(d=1,2,3)为半导体器件所占据的有界区域.
文献[8]在Dirichlet-Neumann混合边界条件下得到了模型(1)~(3)的初边值问题有界弱解的整体存在性,文献[9-10]在Dirichlet边界条件下分别证明了(1)~(3)的一维稳态模型古典解的存在性和唯一性,文献[11]在Dirichlet-Neumann混合边界条件下证明了(1)~(3)的多维稳态模型弱解的存在性. 与(1)~(3)相关的带量子项的模型研究结果见文献[12-15].
本文研究对应于(1)~(3)的双极稳态模型:
-div(θn)=div(n(θ+V)),
(4)
-div(θp)=div(p(θ-V)),
(5)
div((n+p)θ)=(n+p)(θ-θL(x)),
(6)
-ΔV=n-p-C(x),x∈Ω,
(7)
其中电子密度n、空穴密度p、粒子温度θ和电位势V为未知函数;晶格温度θL(x)和杂质密度C(x)为已知函数.
假设区域Ω的边界∂Ω∈C0,1,∂Ω=ΓD∪ΓN,ΓD∩ΓN=∅,ΓN是闭集,ΓD的d-1维Lebesgue测度是正的,即measd-1ΓD>0. ΓD表示半导体器件的欧姆联结部分,ΓN表示绝缘边界部分. 于是,对于模型(4)~(7),提出如下边界条件:
n=nD,p=pD,θ=θD,V=VD,x∈ΓD,
(8)
n·ν=p·ν=θ·ν=V·ν=0,x∈ΓN,
(9)
其中ν表示∂Ω上的单位外法向量.
主要结果叙述如下:
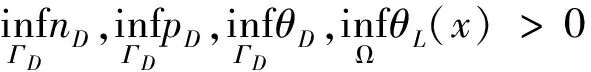
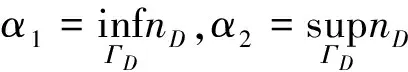
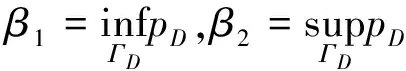

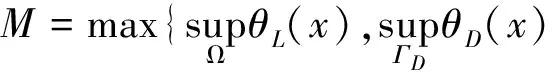
注1 与文献[11]相比较,本文考虑的是双极模型,其耦合性要比文献[11]中的单极模型复杂,对解的先验估计比文献[11]更精细,在利用Leray-Schauder不动点定理证明解的存在性时需要构造不同的不动点算子.
2 结果的证明
由于(4)、(5)、(6)三个方程都是退化的,所以考虑如下截断问题:
-div(θm,Mn)=div(nα1,α2(θ+V)),
(10)
-div(θm,Mp)=div(pβ1,β2(θ-V)),
(11)
div((nα1,α2+pβ1,β2)θ)=
(nα2+pβ2)(θ-θL(x)),
(12)
-ΔV=nα2-pβ2-C(x),x∈Ω,
(13)
其中
nα2=max{0,min{α2,n}},
pβ2=max{0,min{β2,p}},
nα1,α2=max{α1,min{α2,n}},
pβ1,β2=max{β1,min{β2,p}},
θm,M=max{m,min{M,θ}},
α1,α2,β1,β2,m,M的定义见定理1.
定理1的证明需要如下引理.
引理1 设定理1中的条件成立,且(n,p,θ,V)∈(H1(Ω))4是问题(10)~(13),(8),(9)的解,则
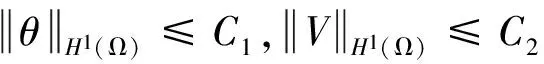
且0<α1≤n≤α2,0<β1≤p≤β2,0
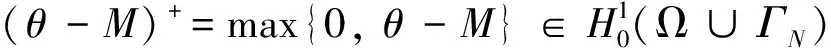
-∫Ω(nα2+pβ2)(θ-θL(x))(θ-M)+dx≤0,

∫Ω(nα1,α2+pβ1,,β2)θ·θDdx-
∫Ω(nα2+pβ2)(θ-θL(x))(θ-θD)dx≤
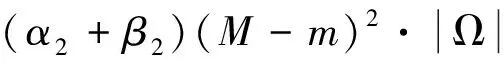
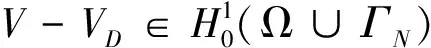
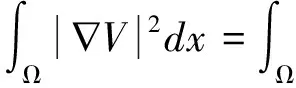
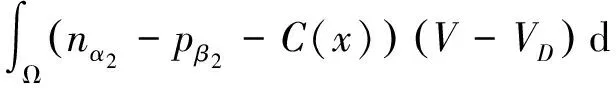
(14)
由带ε的Young不等式和Poincare不等式知
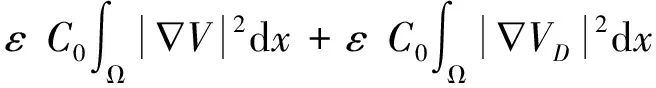
(15)
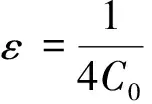
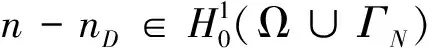
∫Ωθm,Mn·nDdx-
∫Ωnα1,α2(θ+V)·(n-nD)dx≤
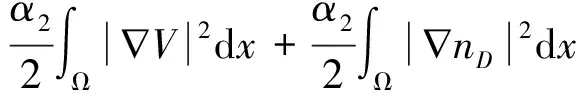
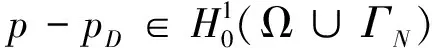
-∫Ωnα1,α2(θ+V)·(n-α2)+dx=0,

同理可证β1≤p≤β2,x∈Ω. 引理1证毕.
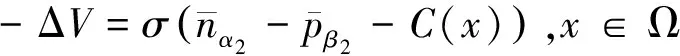
V=σVD,x∈ΓD,V·ν=0,x∈ΓN
的唯一解,这里及后面的σ都满足σ∈[0,1],并设θ∈H1(Ω)是问题
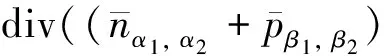

θ=σ θD,x∈ΓD,θ·ν=0,x∈ΓN
-div(θm,M(θ+V)),
x∈Ω,n=σ nD,x∈ΓD,n·ν=0,x∈ΓN
和
-div(θm,M(θ-V)),
x∈Ω,p=σ pD,x∈ΓD,p·ν=0,x∈ΓN
的唯一解. 则算子
T:L2(Ω)×L2(Ω)×[0,1]→
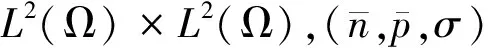
[1] ABDALLAH N B,DEGOND P,GENIEYS S. An energy-transport model for semiconductors derived from the Boltzmann equation [J]. J Stat Phys,1996,84(1): 205-231.
[2] DEGOND P,GENIEYS S,JUNGEL A. An existence and uniqueness result for the stationary, energy-transport model in semiconductor theory[J]. C R Acad Sci Paris,1997,324(1): 867-872.
[3] LI Y,CHEN L. Global existence and asymptotic behavior of the solution to 1-D energy transport model for semiconductors[J]. J. Partial Diff. Eqs,2002,15(4): 81-95.
[4] CHEN L,HSIAO L. The solution of Lyumiks energy transport model in semiconductor science[J]. Math Meth Appl Sci,2003,26(16): 1421-1433.
[5] CHEN L,HSIAO L,LI Y. Global existence and asymptotic behavior to the solutions of 1-D Lyumkis energy transport model for semiconductors[J]. Quart Appl Math,2004,62(2): 337-358.
[6] CHEN L,HSIAO L,LI Y. Large time behavior and energy relaxation time limit of the solutions to an energy transport model in semiconductors[J]. J Math Anal Appl,2005,312(2): 596-619.
[7] LI Y. Global existence and asymptotic behavior for an 1-D compressible energy transport model [J]. Acta Math Sci,2009,29B(5): 1295-1308.
[8] JUNGEL A,PINNAU R,ROHRIG E. Existence analysis for a simplified energy-transport model for semiconductors[J]. Math Meth Appl Sci,2013,36(13): 1701-1712.
[9] 董建伟,琚强昌. 一个一维半导体简化能量输运模型的稳态解[J]. 数学年刊(A辑),2014,35(5): 613-622.
[10] 董建伟,娄光谱,王艳萍. 一个半导体简化能量输运模型稳态解的唯一性[J]. 山东大学学报(理学版),2016,51(2):37-41.
[11] 董建伟,周永卫. 一个能量输运稳态模型弱解的存在性[J]. 华中师范大学学报(自然科学版),2015,49(2): 179-181.
[12] JUNGEL A,MILISIC J P. A simplified quantum energy-transport model for semiconductors[J]. Nonlinear Analysis: Real World Applications,2011,12(2): 1033-1046.
[13] CHEN L,CHEN X Q,JUNGEL A. Semiclassical limit in a simplified quantum energy-transport model for semiconductors[J]. Kinetic and Related Models,2011,4(4): 1049-1062.
[14] DONG J W,ZHANG Y L,CHENG S H. Existence of classical solutions to a stationary simplified quantum energy-transport model in 1-dimensional space[J]. Chinese Annals of Mathematics,Series B,2013,34(5): 691-696.
[15] 董建伟,程少华,王艳萍. 一维稳态量子能量输运模型的古典解[J].山东大学学报(理学版),2015,50(3):52-56.
Existence of weak solutions to a stationary bipolar energy-transport mode
DONG Jianwei, ZHU Junhui, WANG Yanping
(School of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015)
A stationary bipolar energy-transport model for semiconductors is considered. Under the mixed Dirichlet-Neumann boundary conditions, the existence of weak solutions to the above model is obtained by using the truncation method and the Leray-Schauder fixed-point theorem. It is shown that the electron density, the hole density and the particle temperature possess positive upper and lower bound within the domain if they are bounded positively from below and above by the Dirichlet boundary of the domain.
energy-transport model; stationary solution; existence
2016-03-10.
河南省科技厅基础与前沿技术研究计划项目 (162300410077);航空科学基金项目(2013ZD55006);河南省高等学校青年骨干教师资助计划项目(2013GGJS-142);河南省教育厅科学技术研究重点项目(12A110024);郑州航空工业管理学院青年科研基金(2013111001,2014113002,2015113001).
1000-1190(2016)05-0641-04
O 175.2
A
*通讯联系人. E-mail: dongjianweiccm@163.com.
