基于空间计量的城市专利产出绩效研究

杨　鹏，陶小马

基于空间计量的城市专利产出绩效研究

杨鹏，陶小马

中心城市具有强大的集聚效应及辐射效应，其科技创新水平具有很强的代表性。文章在知识生产函数的基础上，以规模报酬可变为前提，采用DEA-M almquist方法分析了我国20个中心城市的专利产出绩效指数及其分解值，并对20个中心城市的专利产出绩效进行实证分析，结果显示：2000-2013年我国20个中心城市的专利产出绩效呈现上升趋势，这种上升趋势主要是由于技术进步所引起的，专利产出绩效值较高的城市主要集中在东部地区，专利产出绩效呈现不均衡性。从空间计量回归结果来看，人力资本、研究与发展经费支出等指标对专利产出绩效具有较明显的推动作用，而研究与发展人员投入指标对于专利产出绩效的提升缺乏显著的贡献。

专利产出绩效；空间计量模型；Malmquist指数

一、引　言

专利从根本上改变了市场竞争的性质和形式，基于专利的竞争日益成为产业竞争成败的关键[1]（P63-64）。新增长理论认为，专利主要通过对研发活动的激励促进创新，进而刺激经济增长。关于专利对经济增长的研究，学者们主要将专利及专利相关指标作为创新或知识产出的重要衡量标准。从研究成果来看，专利对创新具有较强依存度的结论得到了普遍认同，因此用专利来衡量知识和创新是合理和可行的（Kortum,1989；Acs,2002；Furman,2002；马军杰，2013）[2]（P36-42）[3][4][5]。有关专利推动经济增长的研究较早，研究成果较为丰富，多集中分析发明专利或实用性技术在创新和经济增长中的作用，研究结果表明发明专利在发达国家对经济增长具有较为明显的贡献，而在发展中国家则没有这种效果（Schneider,2005；Walter,2008；Yee, 2012）[6][7][8]。国内学者对专利产出绩效的研究大多沿用国外的分析方法，从技术创新的角度分析专利与经济增长之间的关系（李倩，2010；景秀，2013；贺丹丹，2013）[9][10][11]。而对于专利产出绩效的分析则主要集中在创新绩效的理论研究方面（马军杰，2013；吴玉鸣，2006；方曙，2006）[5][12][13]。从研究层面来看，以往的研究大多集中在省域层面，忽视了城市层面的论证分析，尤其是具有较强创新能力和较多专利产出的中心城市，而正是这些中心城市代表了区域创新能力的核心所在。目前的研究大多以独立单元进行观察研究，较少考虑由于空间因素而引起的依赖性和异质性，而这种空间因素对专利产出绩效及科技创新溢出的影响是不容忽视的[5]。克鲁格曼等经济学家的空间经济分析方法已经在省域层面得到了论证，然而由于缺乏关于知识溢出的空间经济微观模型，克鲁格曼的空间经济理论规避了对知识外部性与知识溢出的模型分析。近年来，这些问题得到了学者们的充分重视，已经形成了较为完善的微观空间经济模型。由于知识或技术进步与一个城市或地区的经济发展、科技投入、科研人员数量及专利申请量高度相关，是一种高度聚集的产出，以往的分析从国家或省域层面进行分析，实际是对知识或科技进步的均质化分析。笔者认为，从国家或省的层面来看，科学技术在市域层面的集聚绩效更明显，同时又不能忽略空间依赖性和空间异质性对专利产出绩效所带来的影响。因此，本文选定在科技创新和专利申请方面具有代表性的20个中心城市①对其进行研究分析，以期得出在城市层面的专利产出绩效指数及其影响因素。

二、主要研究方法

（一）知识生产函数

对于专利产出效率的衡量，可以结合知识生产过程来进行设计。这一过程的理论化模型-知识生产函数，则成为考察知识生产效率与知识溢出效应的重要理论分析工具。知识生产函数将创新产出和创新投入联系起来，认为研究与开发经费投入和人力投入是知识生产和创新的主要投入，通过这种投入可以生产出新的有价值的知识。本文拟采用Griliches（1979，1986）和Jsffe（1989）提出的标准知识生产函数[14]（P291-319）[15]，即经过修正的在文献上称之为Griliches-Jsffe知识生产函数的柯布-道格拉斯形式：

其中，K为创新即知识生产函数的产出，RD为R&D支出，Z为其他影响知识生产函数的变量，ε为随机干扰项，i为观测单元数。

（二）DEA-Malmquist生产率指数

Malmquist指数由瑞典经济学和统计学家StenMalmquist在 1953年用来分析不同时期的消费变化时提出的，其后由Caves,Christensen和Diewert（1982）[16]等人将Malmquist指数应用于分析生产率变化的测算，Fare等（1994）[17]给出了非参数的线性规划算法，并和 DEA理论相结合，使得Malmquist生产率指数得到广泛应用。

为了避免由于时期选择的任意性所带来的差异，Caves，Christensen和Diewert（1982）以两个时期Malmquist指数的几何平均值，作为度量t时期到t+1时期生产率变化的Malmquist生产率指数，具体的表达式如下：

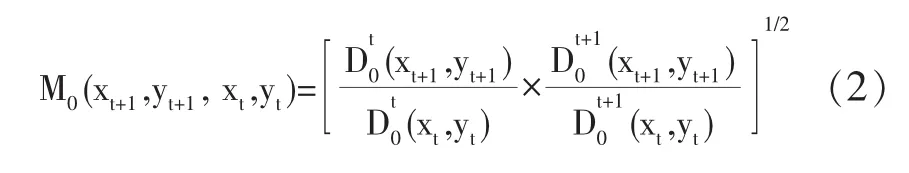
若M0(xt+1,yt+1,xt,yt)＞1，表示全要素生产率呈增长趋势；若M0(xt+1,yt+1,xt,yt)=1，表示全要素生产率不变；若M0(xt+1,yt+1,xt,yt)＜1，表示全要素生产率呈下降趋势。

Nishimizu和Page（1982）将全要素生产率的变化分解为技术进步和技术效率的提高两个不同的组成部分。Fare等（1994）证明，Malmquist生产率指数同样可分解为效率变化指数(effch）和技术进步指数(techch)两部分，并将效率变化指数进一步分解为纯技术效率变化指数（pech）和规模效率变化指数（sech）。

（三）空间计量经济模型

传统的统计理论是一种建立在独立观测值假定基础上的理论，在遇到空间数据问题时，独立观测值在现实生活中并不是普遍存在的（Getis, 1997）。这是因为许多地理空间的数据容易受到空间依赖和空间异质性的影响，使得在应用普通最小二乘法进行模型估计时有可能导致在出现模型设定的偏差（马军杰，2013）。因此，学者通过对地理空间数据进行分析后发现采取空间回归模型可以比较有效地解决空间环境中的空间依赖与空间异质性等问题，这些空间回归模型主要包括系数的空间滞后模型（Spatial Lag Model，SLM）与空间误差模型两种（Spatial Error Model，SEM）（Anselin，1988；Anselin，Florax，2004；李倩，2013）[18]（P137-152）[19]（P283-291）。

空间滞后模型（Spatial Lag Model，SLM）的主要作用是探讨产出变量在一个地区是否具有知识溢出效应，其模型表达式为：

其中参数β反映了自变量对因变量的影响，空间滞后因变量Wy是一内生变量，反映了空间距离对区域经济行为的作用；X为n*k的外生解释变量矩阵，ρ与λ为空间回归关系数，ε为随机误差向量。

空间误差模型（Spatial Error Model，SEM）度量的是邻近地区关于因变量的误差冲击对本地区观察值的影响程度，其模型表达式为：

式中，ε为随机误差项向量，λ为n*1阶的截面因变量向量的空间误差系数，衡量了样本观测值的空间依赖性，即相邻地区的观测值y对本地区观测值y的影响方向和程度，参数β反映了自变量x对因变量y的影响。

判断城市间专利产出绩效的空间相关性是否存在，一般可通过包括Moran's I检验、两个拉格朗日乘数（Lagrange Multiplier）形式LMERR、LMLAG及其稳健（Robust）的R-LMERR、R-LMLAG）等形式来实现。其中Morans I检验的数学表达式如下：

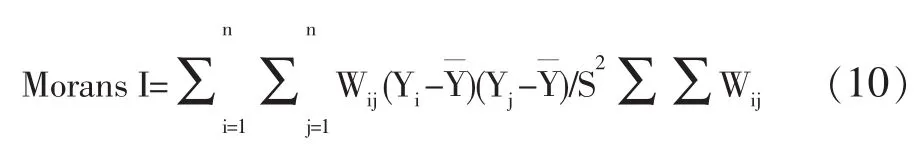
Wi和Wj分别为空间权重矩阵中的第i行和第j列之和，经过变换可得到：Z（d）用于检验n个城市是否存在空间相关关系：当Z值为正且显著时，表明存在正的空间自相关关系，也就是说相似的观测值趋于空间聚集；当Z值为负且显著时，表明存在负的空间自相关，相似的观测值趋于分散分布；当Z值为零时，观测值呈现独立随机分布。

三、基于专利产出绩效的实证分析

（一）DEA-Malmquist专利产出绩效的数据来源与指标选取

本文选取了我国较有代表性的20个中心城市的专利申请量、科技人员数量、研究与发展人员折合全时当量、R&D经费支出占地区生产总值比重、人均GDP等指标。专利数据一般包括专利申请量和专利授权量，而由于专利授权量数据的难获得性并与专利申请量呈现一定的相关关系，故将专利申请量作为体现一个城市的创新产出并作为输出指标，将科技人员总量、科技人员折合全时当量、R&D经费支出占地区生产总值比重作为输入指标。数据主要来源于《中国统计年鉴》（2001-2014年）、《中国科技统计年鉴》（2001-2014年）及各中心城市统计年鉴及科技统计资料等。

（二）DEA-Malmquist专利产出绩效分析结果

本文首先对我国20个中心城市2000-2013年的原始数据进行标准化处理，通过DEA2.1软件得到我国20个中心城市的2000-2013年的综合Malmquist专利产出绩效指数（表1）和20个中心城市的具体Malmquis专利产出绩效指数（表2）。

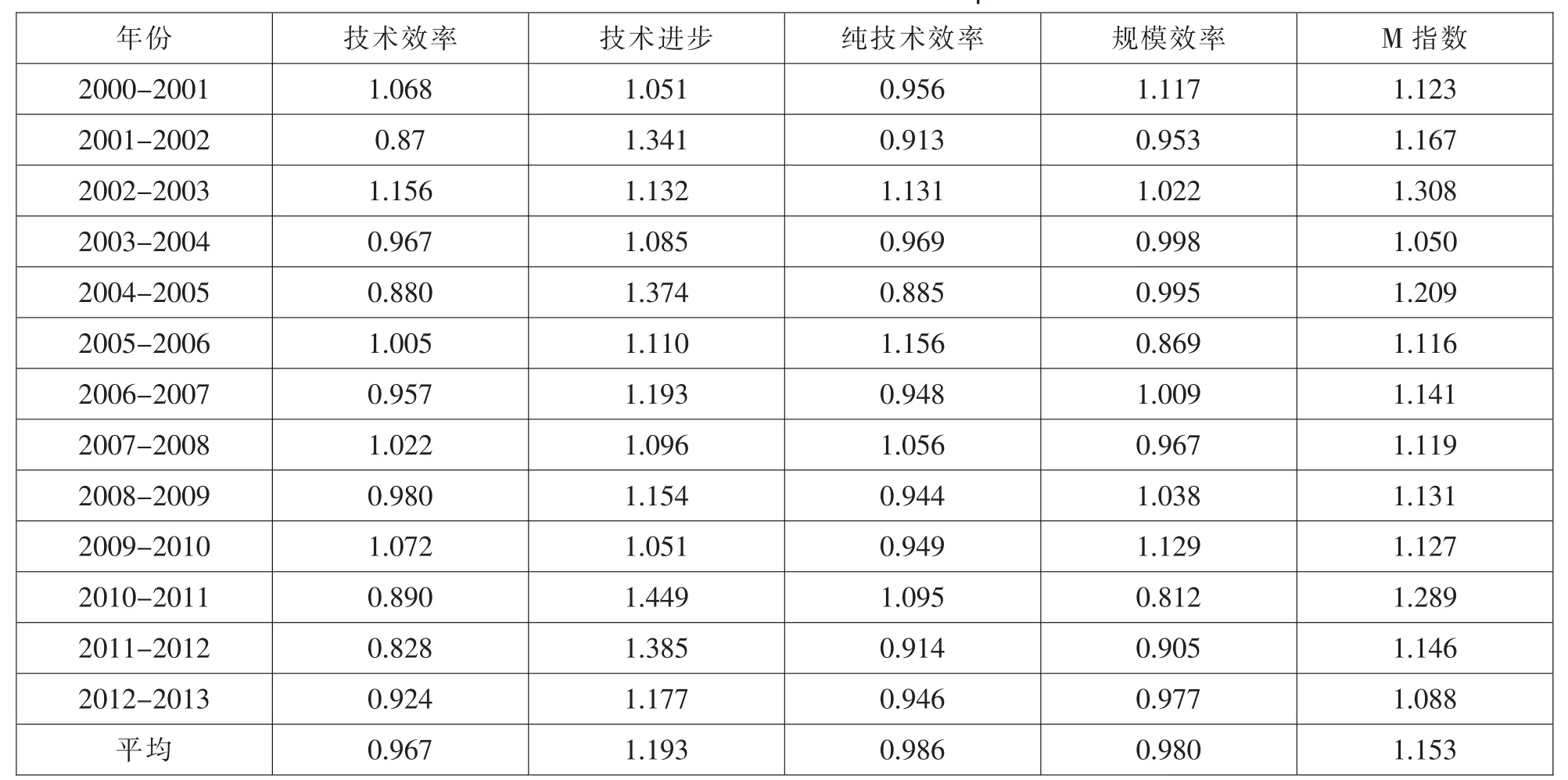
表1　我国20个中心城市2000-2013年DEA-Malmquist专利产出绩效指数

从表1可以看出，我国20个中心城市的Malmquist指数在2000-2013年的14年里虽然有小幅度的波动，但总体均大于1，说明我国20个中心城市的专利产出绩效呈上升趋势，专利产出绩效明显加强。20个中心城市的技术进步效率指数（effch）有小幅度的下降趋势，这说明中心城市的技术效率已经呈现出规模效应递减的趋势。其中纯技术效率变化指数（pech）累计下降1%，规模效率变化指数（sech）累计下降14%，说明技术效率指数下降主要是由于规模效率指数下降所引起的。技术进步指数（techch）累计涨幅12.6%，年均增长1.66%；2000-2013年，我国20个中心城市的Malmquist指数大于1，说明14年内20个中心城市的专利产出绩效呈现上升趋势，但技术效率指数小于1，说明技术效率对Malmquist指数的贡献值在下降，增加1单位技术所带来的专利产出绩效率在下降。从分解值来看，这种下降主要表现在规模效率指数而非纯技术效率上。从2000-2013年我国20个中心城市的平均技术进步指数大于1，说明14年间我国20个中心城市的技术创新能力不断加强，技术进步对Malmquist专利产出绩效指数的贡献不断加大。

将我国20个中心城市的Malmquist指数值按降序排序可得表2。可以看出，各个城市的Malmquist指数值均大于1，表明在这些城市的专利创新绩效较为明显，科技创新能力明显增强。各中心城市的技术进步指数（techch）均大于1，表明专利产出绩效主要是由技术进步提供的。从排名来看，北京、上海、西安、武汉、重庆的Malmquist指数值列20个中心城市的前5位，表明这5个城市的专利产出绩效最为明显，同时在这5个城市的技术进步效率指数和技术进步指数均大于1，纯技术进步指数也均大于1。而上海、西安、重庆3个中心城市的规模效率变化指数小于1，说明在这3个中心城市，由于规模变化所引起的专利产出绩效在下降，从另一方面也可以说明，这些地区的专利产出绩效已达到了规模效应递减的倒U型曲线的右方。

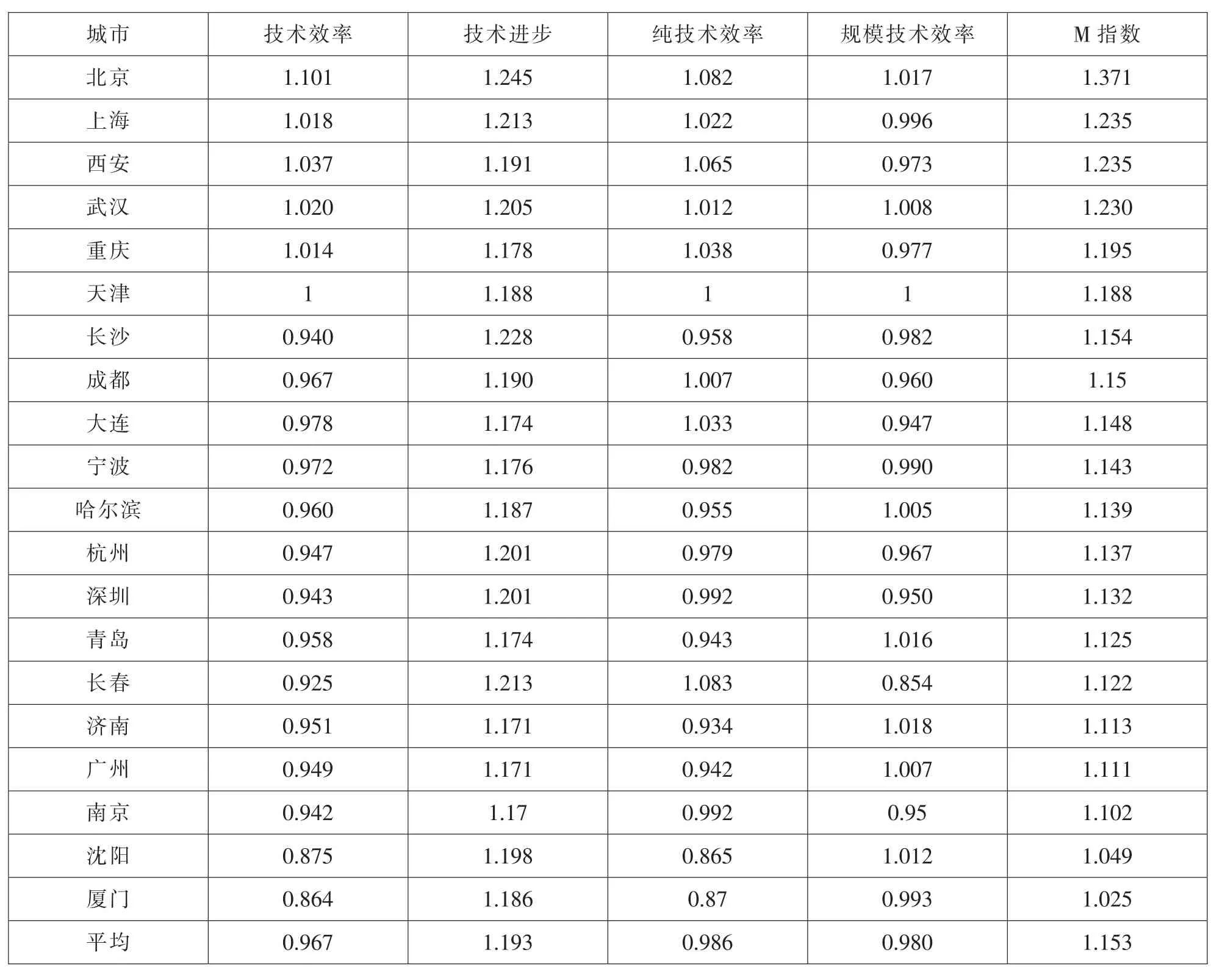
表2　我国20个城市的Malmquist专利产出绩效值及其分解值

四、基于空间计量的专利产出绩效分析

对我国20个中心城市专利产出绩效的成因进行空间计量分析时，首先要对影响专利产出绩效的各种因素进行深入分析，遴选合适的指标构建指标体系。具体如下：一是专利产出绩效（I），本文将专利申请量作为中心城市专利产出绩效指标。二是人力资本投入（X1）。一般认为，科技人员数量与当地的科技创新产出具有较为明显的正相关，本文采用该指标作为衡量中心城市人力资本的指标。三是研究与发展（R&D）人员投入（X2）。R&D人员是科技创新活动的重要推动力量，本文选择研究与发展（R&D）折合全员当量来衡量该指标。四是研究与发展（R&D）经费支出（X3）。由于地区经济发展的不均衡性，单纯地使用该指标并不能体现中心城市的科研投入力量，因此，本文采用研究与发展（R&D）经费支出占中心城市地区生产总值的比重来均衡该指标。

（一）城市专利产出绩效的空间自相关检验

由于本文是基于城市层面的空间计量分析研究，中心城市在地理位置具有明显的不相邻性，为了检验数据是否具有空间依赖性和空间异质性，本文采用空间辐射法，以20个中心城市为辐射点，以省域单元为辐射面，构建省域空间辐射单元，对我国20个中心城市进行空间关联分析。结果显示，2000-2013年我国20个中心城市的Moran's I的指数为0.1755，P值为0.0001，正态统计z值为3.62，大于其在0.01下的临界值（1.96），说明我国20个中心城市的专利数在空间分布上具有正自相关关系，即存在正的空间依赖性，表明我国20个中心城市的专利产出绩效并非表现出完全的随机状态，而是表现出相似值之间的空间集群效应。因此，在对我国20个中心城市专利产出绩效进行分析时有必要将其纳入空间计量模型内分析。

（二）城市专利产出绩效的空间计量结果分析

以市域专利申请量代表专利产出绩效指标（I），并作为被解释变量；以人力资本投入（X1）、研究与发展（R&D）人员投入（X2）、研究与发展（R&D）经费支出（X3）作为被解释变量，构建如下的双对数线性的知识生产函数模型：

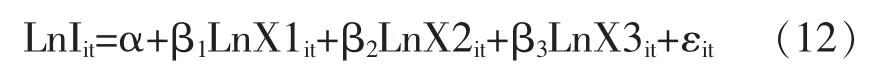
式中：i=1，2…20为中心城市数量，β为回归系数，ε为随机误差项。

通过Moran's I检验可知，我国20个中心城市专利产出绩效具有一定的空间自相关性，因此可以进行空间自相关分析。以式12为模型，首先进行普通最小二乘回归、空间滞后回归和空间误差回归，回归结果如表3。

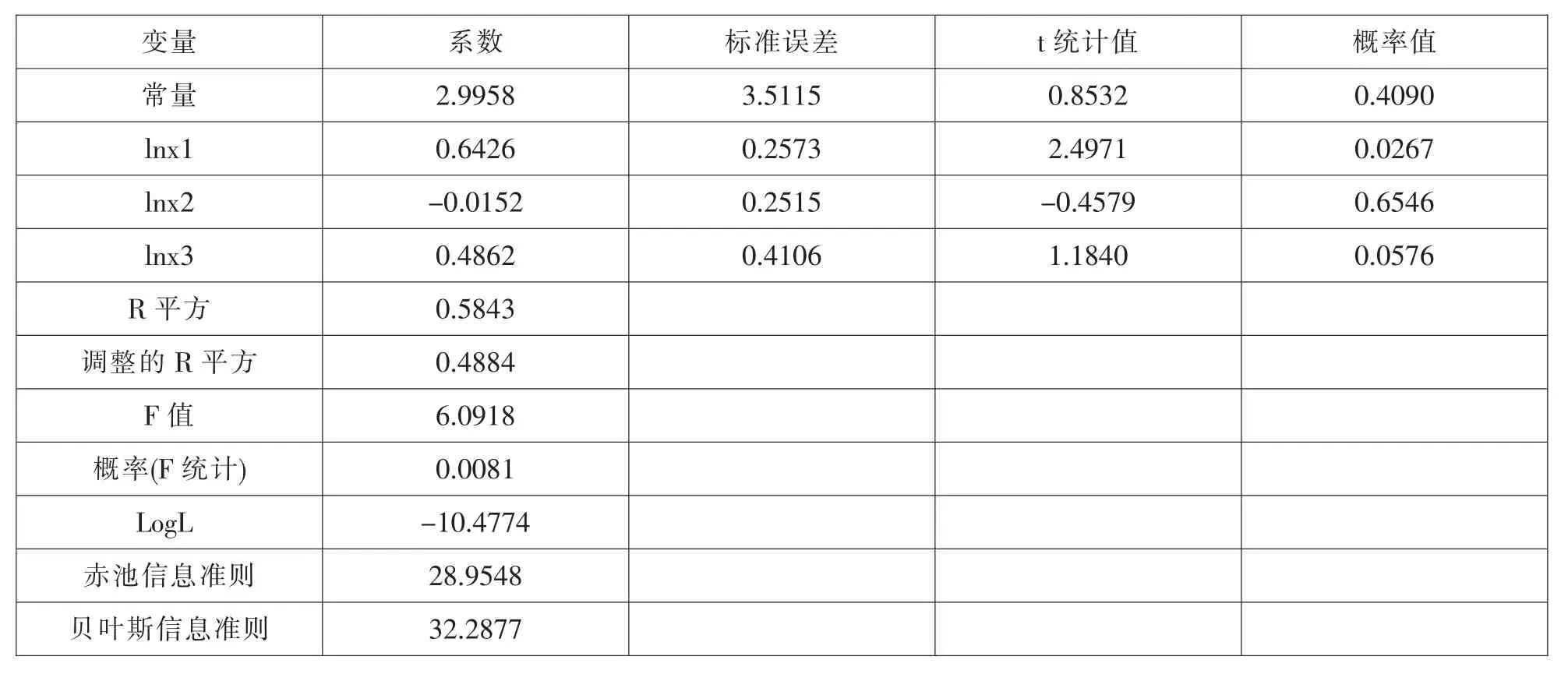
表3　　我国20个中心城市专利产出绩效OLS回归结果

从表3可以看出，OLS的我国专利产出绩效函数的拟合集优度为58.43%，调整后的拟合集优度为48.84%，F值为6.0918，且F统计量的伴随概率为0.008，整体上通过1%的显著性检验。从回归系数来看，lnx1、lnx3和回归系数大于0，而lnx2的回归系数小于0，说明我国中心城市专利产出绩效与人力资本投入、研究与发展经费投入成正相关，与研究与发展人员投入呈现较弱的负相关。从参数的t统计概率可以看出，只有lnx1的t统计概率值小于0.05，常数项、lnx2、lnx3的t统计概率值均大于0.05，表示在5%的显著性检验下不显著。

从表4可以看出，空间滞后模型SLM中的R2为64.1%，大于OLS的58.43%和空间误差模型SEM的62.1%。SLM中的LogL为-9.593，大于OLS中的-10.4774和SEM中的-10.047。SLM中的AIC和SC检验值分别为27.187和30.353，小于OLS（28.954和32.2877）和SEM（28.095和31.428）。因此，可以认为空间滞后模型比普通最小二乘法回归和空间误差模型的模拟效果好。

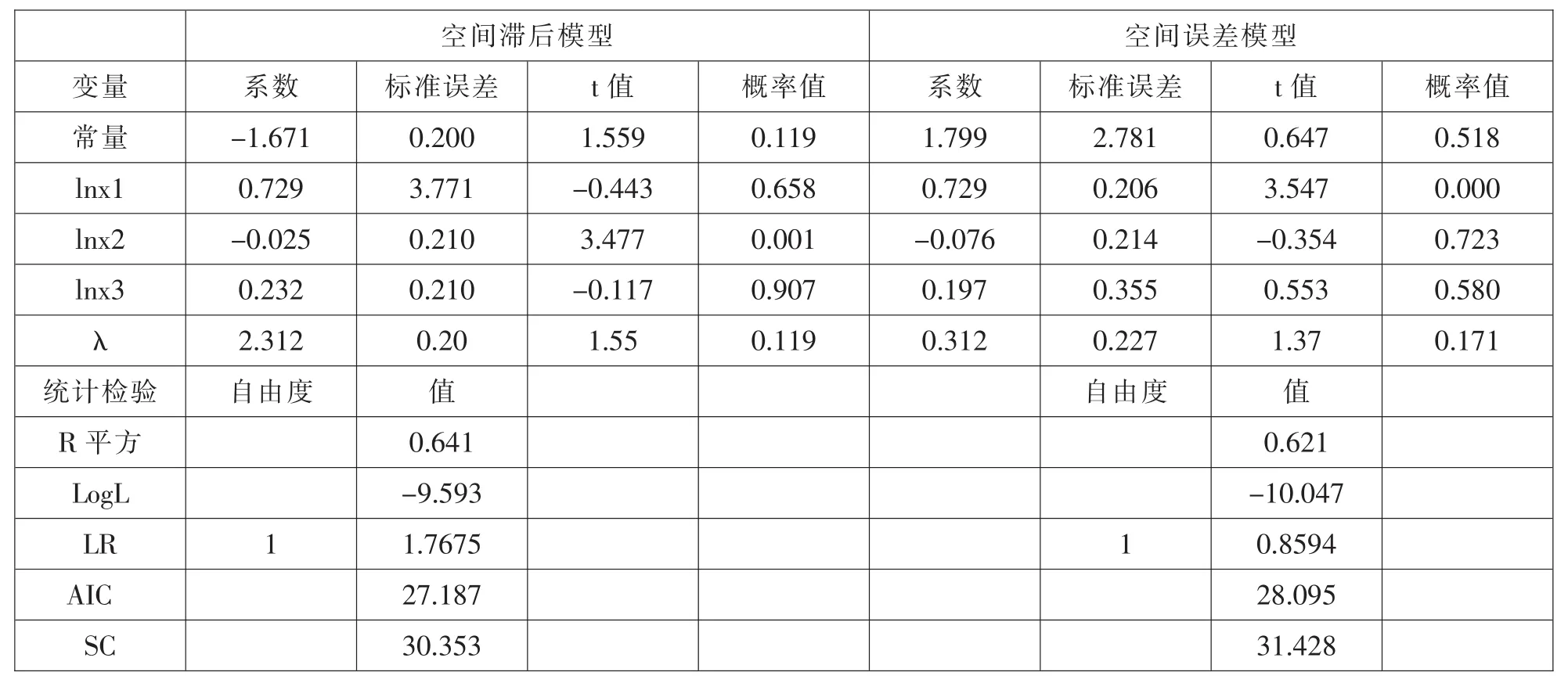
表4　　我国20个中心城市专利产出绩效的空间计量回归结果

从空间滞后模型的结果来看，在0.01的显著性水平下，ρ/λ值为0.344，这意味着我国20个中心城市专利产出绩效存在较为明显的空间自相关性，也就是说，在全局空间内，邻近的中心城市的专利产出绩效表现出较为强烈相似性。

SLM模型和 SEM模型的 LnX1系数都为0.279，说明人力资本特别是科技人员是影响中心城市专利产出绩效的主要驱动因子，这点与本文的预期观点相一致。SLM模型和SEM模型的LnX3的系数分别为 0.486和 1.84，表明研究与发展（R&D）经费支出对中心城市的专利产出绩效有一定的影响。SLM模型和SEM模型的LnX2系数都为负数，这表明在短期内研究与发展人员投入对专利产出绩效的影响较小，这与人们的一般认识存在差别，也与本文的预期不符。一个解释是在短期内，研究与发展人员的研究成果尚无法形成有效的生产力，另一方面也受城市间研究与发展人员投入不均衡的影响，以及在短期内研究与发展人员对专利产出绩效的影响还没有显现所致，选用研究与发展人员投入或许不适合用于解释存在滞后性的专利绩效水平，而对其产生的深层次原因需要做更进一步的研究。

五、研究结论

本文在规模效应可变的前提下，依据全要素生产率的分析框架构建了20个中心城市的DEAMalmquist专利产出绩效指数，并利用分解值分别考察了2000-2013年我国20个中心城市的综合Malmquist专利产出绩效指数及20个中心城市的Malmquist专利产出绩效指数。在此基础上，以知识生产函数为理论基础，对我国20个中心城市的专利产出绩效进行了综合考察，得到如下的研究结论：

一是我国20个中心城市的专利产出绩效在14年内虽然有一定幅度的波动，但总体呈现出上升趋势，这种上升趋势主要来自于技术效率、规模效率和技术进步的共同作用。从Malmquist分解值来看，这种上升趋势主要体现在技术进步指数上，而且技术效率指数和规模效率指数均小于1，并呈现出下降趋势，说明我国20个中心城市的专利产出绩效呈现出较强的溢出趋势。

二是从城市间Malmquist分析结果来看，北京、上海、武汉、西安、重庆等中心城市的Malmquist值分别为1.371、1.235、1.235、1.230、1.195，列20个中心城市Malmquis指数值的前5位，表明这5个中心城市的专利产出绩效较为明显，科技创新能力明显增强。而沈阳、厦门等城市的Malmquist值仅为1.049和1.025，表明其专利产出绩效较弱，同时也说明中心城市专利产出绩效存在一定的不均衡性。从总体来看，专利产出绩效较高的中心城市仍集中在东部地区，但随着时间的推移，中部和西部地区中心城市专利产出绩效在逐步增加。

三是相对于经典的最小二乘回归，空间计量经济学模型特别是空间滞后模型在进行中心城市专利产出绩效形成机制的研究结果更符合客观实际，分析指出，相近的中心城市具有较高的空间相关性。

四是从专利产出绩效的空间计量分析结果来看，人力资本及科研投入对专利产出绩效的影响较大。因此，政府及科技部门应努力增加科研人员数量，加强对科研人员的培育，提高中心城市经济发展中的科技含量。研究与发展的经费支出对专利产出绩效也有较大的促进作用，应着力增加研究与发展经费支出，提升科技创新的质量水平，以科技创新推动城市产业结构的优化升级。

[1]贺化.专利与产业发展系列研究报告[M].北京：知识产权出版社，2013.

[2]KortumS.,Putnam J..Estimating patents nyindustry:PartIand Part II[M].M imeo,Yale University,1989.

[3]Acs,z.,Ardrestch,DB；Feldman,M.Real effects of academ ic research:comment[J].The American Econom ic Review，1982，（1）.

[4]FurmanJ.L.,Porter ME.,SternS..The determ inants of national innovative capacity[J].Research Policy，2002,(31).

[5]马军杰，卢锐，刘春彦.中国专利产出绩效的空间计量经济分析[J].科研管理，2013，（6）.

[6]Schneider.International trade,economic grow th and intellectual property rights:A panel data study of developed and developing countries[J].Journalof Development Economics，2005，（2）.

[7]W alter G.Park.International patent protection:1960-2005 [J].Research Policy，Volume 37，2008，（5）.

[8]YeeKyoung Kim,Keun Lee,W alter G.Park,KineungChoo.Appropriate intellectual property protection and econom icgrow thincountries at different levels of development[J].Research Policy，2012，（3）.

[9]李倩.我国R&D投入强度与产出绩效的关系研究[D].西北大学，2010.

[10]景秀.政府干预、R&D补贴与自主创新产出绩效[D].南京大学，2013.

[11]贺丹丹.江西省高新技术企业科技投入产出绩效研究[D].江西师范大学，2013.

[12]吴玉鸣.空间计量经济模型在省域研发与创新中的应用研究[J].数量经济技术经济研究，2006，（5）.

[13]方曙，张勐，高利丹.我国省（市）自治区专利产出与其GDP之间关系的实证研究[J].科研管理，2006，（2）.

[14]Griliches Z.Parents:Recent Trendsand Puzzles,Brookings Papers on Economic Activity,M icroeconomics[M].Washington,DC:The Brooking Institution,1989.

[15]Jaffe A.Realdffects of academ ic research[J].American Econom ic Review，1989，（79）.

[16]Cave D W,Christensen L R,Diewert W E.Multilanteral comparisons of outpuit,input andproductivityusing superlative index number[J].Economic journal，1982,(92).

[17]Fare,R.,Grosskopf,S.,Norris,M.,Zhang,Z.,Rroductivitygrow th, technicalprogress,and efficiency change in industrialized countries [J].The American Review，1994，（1）.

[18]AnseilnL.Spatialeconometrics:methods and models[M]. Kluwer Academ ic Publishers,1998.

[19]AnselinL,Raymond JG M.Florax Sergio Rey J.Advances in spatial econometrics:methodology,toolsand applications [M].Berlin:Spring Verlag，2004.

[责任编辑：刘烜显]

杨鹏，同济大学经济与管理学院博士研究生，广西社会科学院区域经济研究所研究员，广西南宁 530022；陶小马，同济大学经济与管理学院教授，博士生导师，上海 200092

F290

A

1004-4434(2016)09-0044-07