两空间三角形的退化关系研究
2016-11-29于海燕余沛文何援军
于海燕, 余沛文, 张 帅, 何援军
(1. 东华大学机械工程学院,上海 201620;2. 上海交通大学计算机系,上海 200240)
两空间三角形的退化关系研究
于海燕1, 余沛文1, 张 帅1, 何援军2
(1. 东华大学机械工程学院,上海 201620;2. 上海交通大学计算机系,上海 200240)
通过对两空间三角形关系的分类,讨论了几何退化对几何计算的稳健性的影响力。解决一个问题的第一步是描述这个问题,空间几何退化的完整表述是稳健几何计算算法的设计、改进以及测试的重要基础和保障。首次对空间三角形对的退化进行了深入的研究、全面的梳理。基于投影降维原理,抽取繁杂的空间两三角形关系的规律,分离出完整的空间三角形对的退化样本模型。基本策略是建立计算坐标系,通过投影降维,将空间三角形对的位置关系变成一个固定,只有一个变化的平面位置关系。以相离、接触、相交、内含的线索改变另一三角形的位置和大小,分类出空间三角形对的位置关系,检索出两者的所有退化状态。该方法可以推广到其他三维几何间的退化状态分类和几何计算算法的稳健性设计中。
几何计算;稳健性;退化;三角形求交;投影降维
几何计算处于几何问题的基础层,是曲面、复杂几何体以及其他图形问题处理的计算基础,是科学与工程计算的基础与支撑,在计算机图形学、计算机辅助设计与制造、计算几何以及医学图像处理、建筑设计、运动学与机器人等领域有着广泛应用。计算几何算法的稳健性,尤其是三维空间的几何计算稳健性一直是研究的难点[1-2]。
几何计算的稳健性问题源于理论算法对于输入值的两个简单假设:Real-RAM可获得性假设和输入无退化假设。而在应用中,须要面对由计算机进制产生的浮点运算累计误差和几何本身退化等可能导致的错误。其中退化是几何特有的问题,几何计算的稳健性问题通常特指退化问题[1,3]。国际上已经建立了跨国研究机构,旨在突破这种几何问题特有的计算稳健性瓶颈[4]。近几十年来,在精确计算以及采用扰动法以及二维几何计算方面取得了一些成绩[3,5-6],但对于三维几何计算,由于其空间关系的多变繁杂,仍然没有一个彻底解决的统一方法,令研究人员束手无策[2-3]。关于退化的分析详见文献[3]。解决一个问题的第一步是描述这个问题,然而,在几何计算稳健性问题上,很多情况下,有哪些退化尚不能完全确定,这也是几何计算相对于数计算(numerical computation)的难点所在。因此,空间几何退化的完整表述是几何计算算法稳健性研究的基础和关键。
空间三角形求交测试是几何计算的基本问题之一,在计算机图形学、图像、CAD等领域有广泛的应用。从原始的蛮力(brute-force)方法到经典的Möller和 Held算法,再到由 Roy、Shen、Guigue 和 Troppo提出的算法,三角形求交算法一直是研究的热点[7-12]。经典算法大多几何意义较为明显,涵盖各种几何相对位置的处理算法。近年,随着相关应用领域的不断发展,很多新算法将主要工作集中在如何提高算法的速度。但从算法的描述上,这些新的算法公式繁多,几何意义不明显,很难从理论上检测算法的稳健性。在算法的测试方面,偏重于算法速度的测试,在已发表的文章中很少有算法稳健性的测试与证明。通常的测试方法是用随机产生的三角形样本对算法进行测试,而各种几何退化情况一般不会被检测到,致使检测出现遗漏。实际上,空间两三角形的位置关系比较复杂,退化状态较多[7]。在三角形相交测试中的一个错误可能会导致整个工程不可估量的损失。已经有学者公开指出这种追求速度而放弃稳健性的研究方法及其在工程应用中的问题,明确指出这种只注重速度而忽略稳健性的算法以及随机检测的测试方法是很危险的[13-14]。
本文对空间两三角形的各种位置关系进行全面的梳理,提出了一种基于投影降维的直观分类方法。应用正投影的两面投影表述空间关系,使得空间的“形”得以用平面的投影图穷举出来;以图表达形的方法,便于分类,而且表达直观、便于交流。在保证样本的完整性的基础上,重点考虑退化情况。给出了完整退化样本模型的设计方法和,最后以经典的Möller算法为测试对象,给出了以此退化模型进行算法测试的步骤和注意事项。
1 投影降维
本文采用基于投影降维的可视化分类方法将三角形对的空间位置关系简单直观地描述出来。一个合适的坐标系能够简化几何表述和代数运算,这样的坐标系称为计算坐标系。
计算坐标系通过如下方式建立:对于任意一对三角形A和B,三角形A所在平面定为坐标平面xy(即H面),其法向作为z轴,并以三角形A的一条边作为x轴。
图1表示两个三角形的计算坐标系和在此坐标系下两个三角形对应的3个投影。其中,坐标平面xy对应投影平面H,zx对应V面,yz对应W面,AH表示三角形A在平面H的投影。
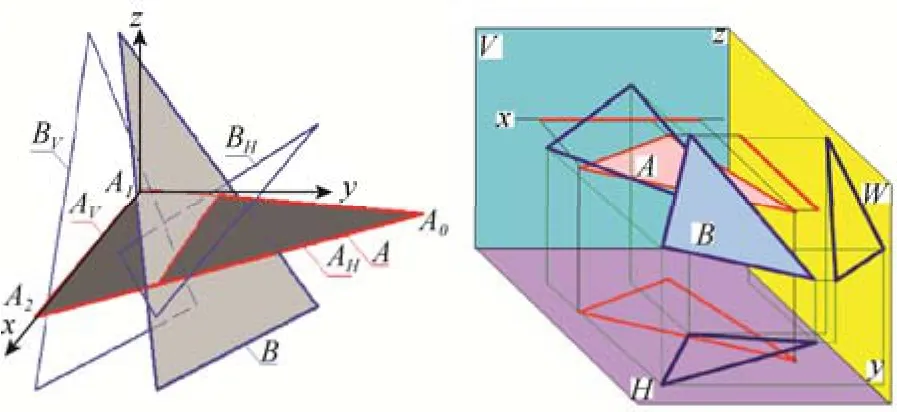
图1 计算坐标系和三角形对的3个投影
在三维坐标系下,一个平面除了不平行、不垂直于任意3个坐标平面之一(称为一般平面)以外还有6种位置状态:①水平面(平行于水平面);②正平面(平行于正平面);③侧平面(平行于侧平面);④垂直于水平面;⑤垂直于正平面;⑥垂直于侧平面。
如果把三角形A固定在水平面上,在计算坐标系下,三角形A在V和W面的投影都是线段,在H面的投影是其本身;三角形B的投影可能是线段或者三角形。三角形A和B这7种空间位置关系、两三角形所在平面的位置关系以及对应的各面投影归纳如表1所示。其中,L表示线段,△表示三角形,PA表示三角形A所在平面,PB表示三角形B所在平面。

表1 三角形A和B的投影关系
2 模型样本设计
首先,根据两三角形所在平面的关系进行分类,分为平行、共面和相交3类。若两平面平行,则两三角形必定分离。若两平面共面,则在H面上的投影即反映两三角形空间关系。若两平面相交,则固定三角形A,通过改变三角形B的平面,得出两三角形平面的各种空间位置关系,并由两个投影对应其空间关系。这样,投影可以分为线段与线段、线段与三角形这两种类型。最后,通过改变三角形B的相对与三角形A的位置或大小得到投影面上典型的相对位置关系;对于两个平面相交的,再通过两个投影面的排列组合得到所有典型的空间位置关系。
2.1 两三角形所在平面共面
为寻求最佳吸尘孔径尺寸,探究吸尘孔孔径大小对除尘效果的影响,特建立孔径分别为1、20、25 mm的掘进机截割部模型,探究同转速、同行进速度下孔径大小对除尘效果的影响。具体方案见表2。
当两三角形位于同一平面时,属于表1的t-1,在H面的投影情况就是实际的空间位置关系。重点讨论所有的几何退化情况:点点碰撞、点线碰撞、线线碰撞以及一些容易判断出错的情况,如图2所示。

图2 平面内两三角形典型位置关系
2.2 两三角形所在平面相交
当两三角形所在平面相交时,两三角形平面的位置关系可为表1中的t-2到t-7,三角形A和B的投影关系在3个投影面有L-L,L-△和△-△ 3种,选择两个相对简单的投影关系描述空间状态。据此,将两面投影关系进一步分为3类:①表1中的t-2、t-3、t-4、t-5,两面投影关系为L-L/L-△;②表1中的t-6,两面投影关系为L-△/△-△;③表1中的t-7,三角形B的平面为一般位置。
2.2.1 类型①的分类方法
以t-2为例,首先选取V/W两投影面描述空间状态。然后,在V面上移动三角形B得到3种位置关系,如图3所示。在W面上移动三角形B,得到9种位置关系,如图4所示。最后,通过两个面的组合得到所有位置关系。例如,当在V面的位置关系如图3(a)所示时,W面上所有的位置关系都可能出现,所以此种情况有9种;同理,图3(b)也对应9种;图3(c)中除了图4(h)所示的位置关系不会出现外都会出现,所以有8种。综上,t-2有26种位置关系。当选择图3(a)和图4(b)进行组合,那么实际的空间位置关系为图5(a)所示,显然,两三角形不相交。同理,图5(b)由图3(b)和图4(e)组合而成,此处为线面碰撞的几何退化情况。图5(d)由图3(b)和图4(e)组合成,虽然图3(b)和图4(e)均相交,但是实际不相交。对于图5(e)同样如此。从图5中可以看出,若两三角形在两投影面都不相交,则空间一定不相交;即使两三角形在两投影面均相交,空间也不一定相交。
对类型①的其他类型,如t-3、t-4和t-5,分类方法与t-2相同。例如,对 t-3,选取 V/W两投影描述对应空间状态。在W面上移动三角形B得到3种位置关系,如图6所示。在V面上移动三角形B,得到类似于图4的9种位置关系。此类的组合情况与 t-2完全一样,也有 26种位置关系。

图3 三角形B垂直于V面时V面的投影关系
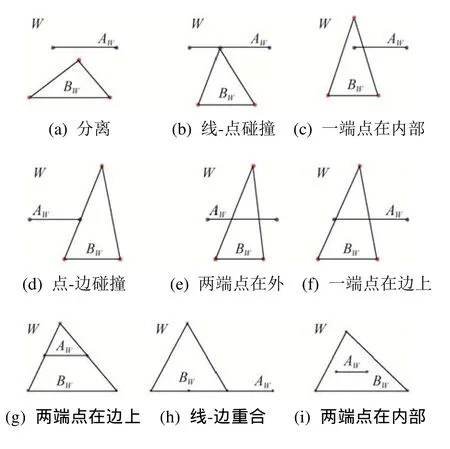
图4 三角形B垂直于V面时W面的投影关系
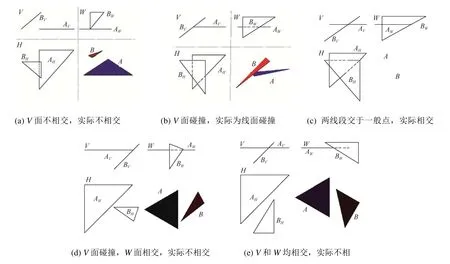
图5 t-2中一些典型的位置关系

图6 三角形B为正平面时W面的投影关系
在t-6中,由于所有面的投影关系均为L-△,所以t-6单独归为类型②。选取H/W两投影面,其两面的投影关系均与图4一样。将两投影面关系进行组合,排除重复的,得到36种位置关系。
2.2.3 类型③的分类方法
在t-7中,由于三角形B处于一般位置,采用随机三角形产生测试样本。
根据以上的分类方法,t-1有7种位置关系,t-2,t-3,t-4和t-5均有26种,t-6有36种,则稳健性测试样本一共有147种位置关系。其中有81对相交,66对不相交。
3 模型样本的建立
通过以上分析,得到了147种三角形求交测试样本,包括了表1中的前6种类型,涵盖各种可能出现退化的情况。这种分类方法以及模型样本可作为三角形求交算法设计的依据和参考,也可以作为测试样本,供算法测试使用。文献[15]将这种分类方法与算法设计相结合,提出了一种基于投影降维的三角形求交算法,详细分析了各种退化情况,并最终给出了统一的算法。
4 模型样本分析及应用
以下给出在算法测试上的应用方法。
几何计算算法测试一般包括稳健性测试和速度测试。两种测试目标不同,应分别设计不同的测试样本。以上得到的t-1到t-6的147种位置关系包含了各种特殊位置状态,可以作为稳健性测试样本。对于表1中的t-7类型,即两三角形处于一般位置状态,可采用随机测试方法得到若干数据,可作为速度测试的补充样本。这样,特殊位置关系的逐级分类表述设计,辅以大量随机数据,整个测试样本包括了两三角形所在平面平行、相交及共面3种位置关系,及每种位置关系下两投影的各种组合关系,对应得到各种空间位置关系。
测试流程上,可先作稳健性测试,测试通过后可对各种不同相交率进行速度测试。表2给出了采用上述方法对经典的 Möller算法的测试结果,供其他算法测试对比参考。测试硬件条件为:Intel Core i3 CPU M 370;2.4 GHz;内存1.92 GB;Windows XP操作系统。稳健性测试使用147种测试样本。速度测试,取11种相交率(0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0),分别对每种相交率取5个数据样本集,每个样本由5 000个三角形对组成,5个样本重复测试1 000次,测试完成后取均值得到每种相交率的测试时间。

表2 不同相交率的平均测试时间
几何计算算法的不稳健主要由 2种原因导致:①几何问题本身引起的,源于几何元素和关系的一般性假设,对于特殊状态和关系的忽略或遗漏导致);②源于计算机的有限计数制,对实际中的数值的截断有累计误差导致。累计误差导致的错误也常常发生在退化情况。因此,在算法设计与测试中,还应相应地对计算精度进行处理。例如,实际测试中,曾检测出有3对三角形关系判断错误,如图7所示。这3对三角形位置关系恰好都是处于相交与不相交的临界状态,运算过程中变量产生的误差将逐渐累积,最终导致有效数字最后位数与没有截断误差时不同,即判断出错。将坐标值都缩小100倍后(此时坐标值均小于10),测试结果恢复正确。累计误差一般采用精确计算方法解决,可以参考文献[16]。

图7 坐标值扩大后测试出错的3对三角形
5 总结与讨论
本文提出了一种直观的空间三角形对的分类方法,重点考虑几何退化导致的稳健性问题的测试。首先给出了计算坐标系的建立方法,然后给出了分类的依据和用两投影描述空间关系的方法。并由此设计出了一套以图形表达的、涵盖各种可能影响几何稳健性情况的直观完整的退化模型。将复杂的空间关系转换为平面上简单直观的线段与线段、线段与三角形的几何关系,这种投影降维的几何方法描述直观,几何意义明显,便于交流。本文将空间的“形”,借助投影降维的方法与两投影图建立了相互对应的关系,进而由两投影图推演表述出各种可能的空间退化。这种对空间几何关系的降维梳理及投影图表述方法,可推广到其他三维几何计算算法的稳健性测试甚至几何计算算法本身的设计上。为三维几何计算稳健性算法研究提供了一种新的途径。
[1] Schirra S. Precision and robustness in geometric computations [M]//Lecture Notes in Computing Science. Berlin:Springer Press, 1997: 255-287.
[2] Halperin D. Robust geometric computing in motion [J]. The International Journal of Robotics Research, 2002, 21(3): 219-232.
[3] Mehlhon K, Osbild R, Sagraloff M. A general approach to the analysis of controlled perturbation algorithms [J]. Computational Geometry: Theory and Application, 2011, 44(9): 507-528.
[4] The Computational Geometry A lgorithms Library. The cooperative association for internet (CGAL) [EB/OL]. [2015-05-04]. http://www.cgal.org.
[5] Sacks E, Milenkovic V, Kyung M K. Controlled linear perturbation [J]. Computer-Aided Design, 2011, 43(10): 1250-1257.
[6] Ozaki K, Ogita T, Oishi S. A robust algorithm for geometric predicate by error-free determ inant transformation [J]. Information and Computation, 2012, 216: 3-13.
[7] Möller T. A fast triangle-triangle intersection test [J]. Journal of Graphics Tools, 1997, 2(2): 25-30.
[8] Held M. ERIT-A collection of efficient and reliable intersection tests [J]. Journal of Graphics Tools, 1998, 2(4): 25-44.
[9] Tropp O, Tal A, Shimshoni I. A fast triangle to triangle intersection test for collision detection [J]. Computer Animation and Virtual Worlds, 2006, 17(5): 527-535.
[10] Devillers O, Guigue P. Faster triangle-triangle intersection tests [R/OL]. [2015-03-05]. http://citeseerx.ist.psu.edu/ viewdoc/download?doi=10.1.1.6.1725&rep=rep1&type=pdf.
[11] Guigue P, Devillers O. Fast and robust triangle-triangle overlap test using orientation predicates [J]. Journal of Graphics Tools, 2003, 8(1): 25-32.
[12] Hao S, Heng P A, Tang Z H. A fast triangle-triangle overlap test using signed distances [J]. Journal of Graphics Tools, 2003, 8(1): 17-23.
[13] Robbins S, Whitesides S. On the reliability of triangle intersection in 3D [C]//Computational Science and Its Applications — ICCSA 2003. Berlin: Springer Press, 2003: 923-930.
[14] Ericson C. Triangle-triangle tests, plus the art of benchmarking [EB/OL]. [2015-03-01]. http://realtimecollisiondetection.net/blog/?p=29.
[15] 于海燕, 何援军. 空间两三角形的相交问题[J]. 图学学报, 2013, 34(4): 54-62.
[16] Fortune S. Polyhedral modeling with exact arithmetic [C]//SMA’ 95 Proceedings of the third ACM symposium on solid modeling and applications. New York: ACM Press, 1995: 225-234.
Degeneracy Relations for Two Spatial Triangles
Yu Haiyan1, Yu Peiwen1, Zhang Shuai1, He Yuanjun2
(1. College of Mechanical Engineering, Donghua University, Shanghai 201620, China; 2. Department of Computer Science & Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
This paper discussed degeneracy and robustness issues in geometric computing by an example of two 3D triangle pairs intersecting ,especially the classification of their various relations. The first key to a problem is to describe this problem. Hence, the complete representation of degeneracies is an important foundation and support to design, improve as well as test a robust geometric computing algorithm. For the first time, this paper studies degeneracies for various triangle pairs in 3D space. Based on projecting reduction, their relationships are classified and a complete sample model is deduced to cover all kinds of degeneracies. The basic strategy is to establish a computed coordinate system. Then by projection, 3D relations are reduced to planar ones. Fixing one triangle, and changing the relative position and size of the other, various relations are classified in the clue of departed, contacted, intersected and overlapped. Consequently, all degeneracies can be got. The method proposed in this paper provides a new way to robustness 3D geometric computing algorithms not only for testing samples but also for algorithm reform ing.
geometric computing; robustness; degeneracy; triangles intersection; projection and reduction
TP 391.72
10.11996/JG.j.2095-302X.2016030349
A
2095-302X(2016)03-0349-06
2015-08-11;定稿日期:2015-11-13
于海燕(1974–),女,黑龙江海林人,副教授,博士。主要研究方向为CAD/CG。E-mail:yuhy@dhu.edu.cn
