基于IIF模型的流体表面张力模拟

董兰芳， 章 恒， 陈骏雄

(1. 中国科学技术大学计算机科学与技术学院，安徽 合肥 230027；2. 浙江大学流体动力与机电系统国家重点实验室，浙江 杭州 310027)

基于IIF模型的流体表面张力模拟

董兰芳1,2， 章 恒1， 陈骏雄1

(1. 中国科学技术大学计算机科学与技术学院，安徽 合肥 230027；2. 浙江大学流体动力与机电系统国家重点实验室，浙江 杭州 310027)

基于光滑粒子动力学(SPH)方法模拟流体时流体表面张力的作用在固液、气液交界处不可忽视，其影响模拟的准确性和视觉真实感。目前已有的表面张力模型如连续表面力(CSF)模型、粒子间相互作用力(IIF)模型都存在各自的缺陷。针对 IIF模型模拟表面张力时所产生的粒子非物理聚集、流体表面形状不规则等现象，采用基于类Lennard-Jones势函数的分子间聚斥力对表面张力建模，并定义了基于法向差的SPH张力修正项以解决IIF模型不能保证流体表面面积最小化问题。实验结果表明，该方法能够稳定和正确地模拟两相交界处的表面张力的效果。

计算机图形学；流体模拟；光滑粒子动力学方法；表面张力；粒子间相互作用力模型

表面张力作为流体的一种常见和重要的物理性质，随着对流体细节和模拟精度要求的增强，在诸如计算机图形学领域和工程数值计算领域对表面张力的模拟也越来越重视。从微观层面说，表面张力的产生是由于表面区域的水分子受到各种方向分子间作用力的合力不为零，指向流体内部。从宏观表现上看，根据拉普拉斯定律，表面张力的作用就是最小化表面区域面积，如自然界中液滴的形成、聚合和分裂。

光滑粒子动力学方法(smoothed particle hydrodynamics, SPH)作为一种典型的拉格朗日流体模拟方法，由于具备相较于传统基于网格方法的易编程、方便处理复杂边界和大形变问题等优点而被广泛应用于流体模拟领域[1-3]。目前基于SPH的表面张力模拟方法主要分为两种：基于连续表面力模型(continuum surface force, CSF)和基于粒子间相互作用力模型(inter-particle interaction force, IIF)。CSF模型是将作用在流体表面上的力转换为周围流体体积力，最早由Morris[4]在2000年提出，并与基于网格的流体体积函数 (volume of fluid, VOF)方法进行了对比，得到可信的结果。在Morris的基础上，Müller等[5]采用颜色域函数对其进行简化，Hu和Adams[6]则通过配置新的粘性项，解决了速度和剪切应力在多相交界处的连续性问题。2011年强洪夫等[7]采用SPH方法中解决边界核函数插值问题的校正平滑粒子方法(corrective smoothed particle method, CSPM)对CSF模型中表面张力计算进行修正，并对二维溶液中油滴的碰撞破碎过程进行了模拟。如文献[7]所述，CSF模型模拟表面张力时在尖角、边界粒子缺失严重的部位曲率计算误差很大，需要花费额外的计算代价来进行修正。另外，CSF模型以一种非对称的形式将力施加到SPH粒子上，这使得流体的动量不再守恒。

IIF模型是一种基于分子间相互作用力，从微观尺度上模拟表面张力产生的模型。在流体内部，分子受到的周围领域内分子在各种方向上作用力的合力为零，与此同时，处于流体表面的分子仅受到流体内部分子的作用力而导致合力非零，宏观表现为表面张力。SPH方法模拟表面张力时，将流体用粒子表示，应用IIF模型思想则对每对粒子施加一对对称的作用力[8-9]，在粒子分布近似均匀的前提下，对整个流体系统施加这一作用力可近似模拟表面张力效果。文献[8]和[9]的不同之处在于采用不同的分子间作用力模型。IIF模型克服了CSF模型的缺点，不再需要计算曲率，因此编程简单，计算效率高。同时由于对称形式作用力的引入保证流体的动量守恒。然而实验证明，仅仅引入粒子间相互作用力不能保证表面区域面积趋向最小，因为流体平衡状态可以在非最小表面面积状态下达到。

本文所基于IIF模型的表面张力模型，采用基于距离的类 Lennard-Jones势函数为粒子间作用力建模。同时，为了解决IIF模型不保证表面面积最小问题，利用文献[5]中的一些结论引入了一个张力修正项，通过对立方体液滴在去除重力下形变过程的模拟，得到了与文献[7]中修正后的CSF模型几乎一致的结果，证明了该方法的正确性。通过对碰撞破碎过程对比和多液滴合并的模拟证明该方法的有效性。

1 流体模拟框架

1.1 SPH基本形式

SPH方法中用粒子来承载诸如密度、质量等各个物理量，连续的流体场被离散成大量独立的粒子，流体连续的物理量根据周围流体粒子相对应的物理量插值得到。SPH方法中的核函数用于确定空间中周围粒子对中心粒子插值的权重，一般来说，核函数的选择使得离中心粒子越近的粒子插值权重越大。SPH基本离散化的形式[10]为：

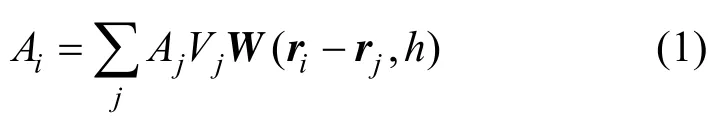
其中，W为插值所用的光滑核函数；h为其核半径；ri和rj分别为粒子i、j的位置；Aj为粒子j所对应的物理量；Vj为粒子j的体积。

以当前粒子为中心，h为半径的球体范围称为当前粒子的支持域。直观上，SPH方法通过枚举支持域内所有粒子以用于插值，从而得到当前粒子的相应属性值。

1.2 SPH流体运动方程

流体运动用经典的Navier-Stokes方程来刻画，如式(2)所示：

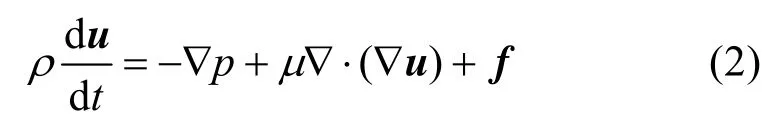
其中，ρ为流体的密度；u为速度矢量；p为压强；μ为粘力系数；f为合外力项诸如重力和浮力等。

基于文献[6]用SPH方法离散化Navier-Stokes方程，先将密度项根据粒子的分布计算出来，再用于计算压力项和粘力加速度项，如式(3)～(5)所示。

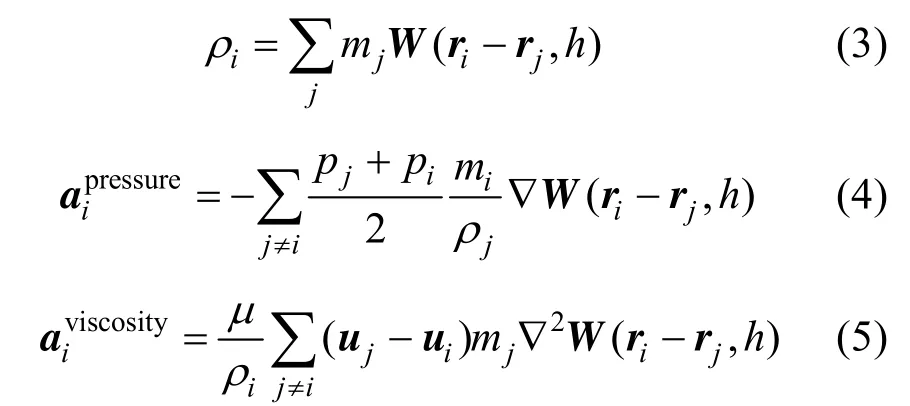
为了从密度求出压强，采用文献[9]提出的弱可压缩法(weakly compressible SPH，WCSPH)，模拟时间步长根据CFL条件[10]来估计。对于在流体与空气交界处表面由于缺少邻居粒子，导致密度估计失真而产生的拉伸不稳定现象，采用Shepard filter来对流体密度进行平滑。对于在流体与固体交界处为了避免 sticking particles问题，采用文献[11]中利用单层固体边界粒子对周围邻居流体粒子进行密度校正的方法解决。

2 修正的IIF表面张力模型

流体的表面张力由分子间的内聚力产生，然而，在采用单纯的IIF模型模拟SPH流体是在宏观层面上考虑粒子间的相互作用力，由于对称的粒子作用力的引入，整个流体系统的动量是守恒的，流体系统的平衡态可以在流体的任意形态达到，这样导致的结果就是流体表面区域面积的最小化难以保证，需要通过其他手段来进行修正。本文中表面张力模型中采用一个类Lennard-Jones势函数为粒子间的聚斥力建模，同时考虑使得表面区域最小化的表面力项。

2.1 粒子间聚斥力模型

IIF模型中为粒子间施加一个基于粒子间距离的作用力，基本形式如式(6)所示，Fcohesioni＜-j描述粒子j对粒子i的作用力。其中，mi和mj是粒子i和j的质量，L(d)是一个核函数控制粒子间作用力的正负(分别对应着排斥力和吸引力)，文献[8]最早提出基于一个类余弦函数的粒子间聚斥力，但该函数在粒子距离 d趋于0时，函数值也趋于0，意味着粒子间的排斥力随着距离的减小而减小，这会导致在模拟弱可压缩流体时出现非物理聚集现象。文献[9]采用一个SPH核函数来为粒子间吸引力建模，由于缺少排斥力项，该模型也会导致非物理聚集现象的发生。本文采用文献[12]中模拟流体和可变形固体交互时流固间作用力所使用的类Lennard-Jones势函数作用核函数：

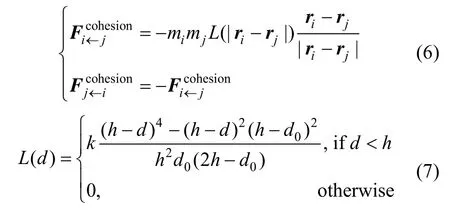
其中，h为作用范围；k为控制表面张力影响程度的系数；d0为静止距离；d为当前两粒子间距离。

式(7)中不同作用范围下L(d)的值随粒子间距离d的变化而变化(图1)，其中系数k值取0.001，d0值取4×10-3mm，h分别取1.5 d0, 2 d0, 2.5 d0。

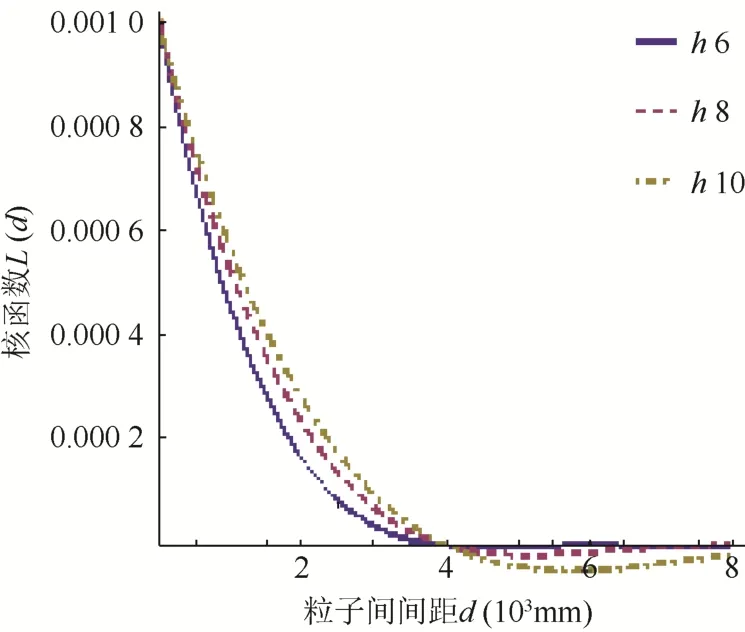
图1 不同作用范围下L(d)随粒子间距的变化

由图1可见，当d=d0时，粒子间作用力为0，当 h＞d＞d0时,函数值为负，表现出吸引力，当0＜d＜d0时，函数值为正，变现为排斥力。另外,当d趋于 0时，函数值趋于 k，这样避免了文献[8] 和[9]中的非物理聚集现象发生。

2.2 表面张力修正项

基于类Lennard-Jones势函数的粒子间聚斥力可以有效地解决粒子非物理聚集的问题，并且保证动量守恒，但不能保证表面面积最小化。为了解决这个问题，本文引入一个表面张力的修正项：

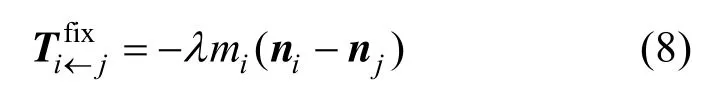
其中，mi为当前粒子i的质量；ni和nj分别为粒子i处的法向和粒子j处的法向；λ为修正项系数。

该修正项的思想受文献[13]中的分析启发，从离散的观点来说，表面张力趋向于将一个局部区域内所有离散采样点的法向变得一致。直观地说，即抚平该区域的曲率。对于粒子 i，的意义在于作用于粒子i，使得i和j之间的法向差变小，推广到整个计算域中所有流体粒子，项的施加将使得曲率大的地方(即流体表面)的法向差变小，即减小曲率，从而最小化表面面积。推广到整个计算域上，粒子i的表面张力修正项用SPH形式表示有以公式：

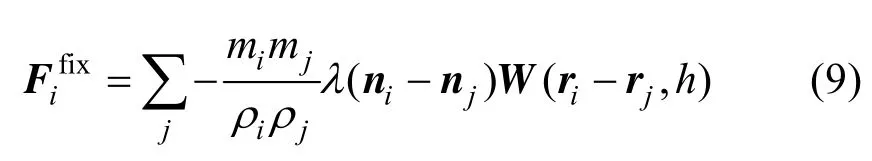
其中，Ffixi为粒子i的表面张力修正项。

对于一对粒子i和j而言：

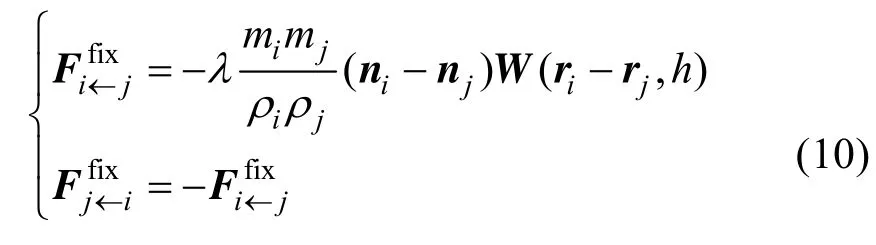
粒子间的表面张力修正项也是对称的，因此修正项的引入不破坏动量守恒条件。关于粒子法向的计算，采用文献[5]的方法，即先为整个计算域定义一个颜色域函数，然后计算颜色函数的梯度，得到的梯度函数就是计算域上每处的未归一化法向。用SPH的形式表示如下：

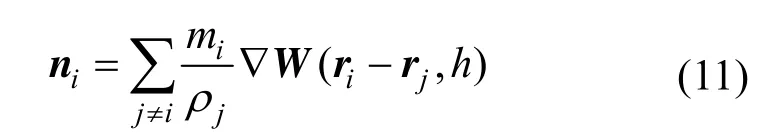
在CSF模型中，通过每个粒子处法向的散度来估计该处的曲率，然后定义一个大小与曲率相关，方向为法向的力，即该粒子处所受到的表面张力。整个过程需要对法向进行归一化，而在流体内部，对法向归一化可能导致流体内部的法向计算不准确，从而需要额外处理来修正。在本文模型中，由于避免了直接计算粒子处的曲率，从而也无需对法向进行归一化，因此也就不需要进行额外的处理。

3 算法实现和参数选择

本文模型中计算每个粒子的表面张力时需要考虑周围邻居粒子的贡献，所以对表面张力的模拟是耦合在流体模拟框架中的。单独来看，具体步骤如图2所示。

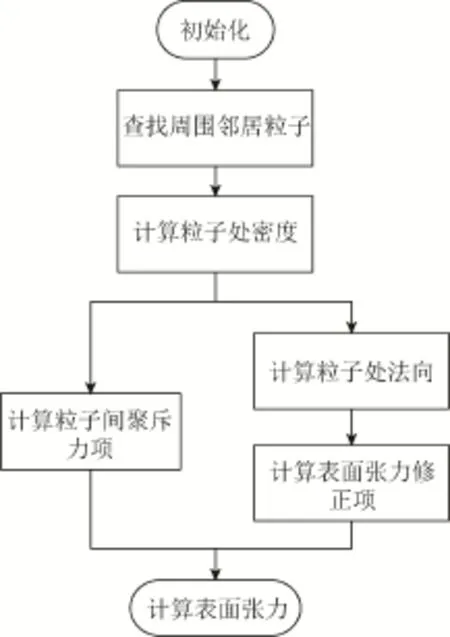
图2 表面张力模拟流程

关于 SPH流体的模拟，采用文献[6]和[14]中所设计的几个多项式核函数，针对计算不同物理量选取不同的核函数。SPH的光滑核半径取值为1.5R，R是 SPH粒子的直径，粒子半径的选取与采样流体所使用的粒子数有关，压强的计算采用文献[9]中的WCSPH方法，时间步长的选择根据CFL条件[10]来估计，在实验中时间步长设为0.005 s。数值积分采用简单的leap-frog模式[15]。关于表面张力模型中涉及的2个主要参数：类Lennard-Jones势函数中的聚斥力缩放系数 k和表面张力修正项中修正系数λ，这两个模型参数都是经验值。实验表明，两个参数的取值应在同一数量级上，在实验中将其保持与流体的粘度系数一致(0.001)，能够在维持流体粒子的1%密度震荡幅度的同时取得良好的可视化效果。

4 实验算例和结果

实验配备 2.8 GHz Intel Core i5-2300 四核CPU和GeForce GTS 450显卡以及4 G内存的硬件机器，流体粒子形式的渲染基于OpenGL平台实时绘制。

4.1 立方体液体形变为规则球体

算例1. 模拟了0.5×0.5×0.5(m3)的水柱在无重力的情况下由表面张力驱动，形变成规则球体的过程，其中流体粒子4 913个。在无重力等外力的情况下，流体稳定状态下的形状主要由表面张力决定，表面张力使得流体各个地方的曲率趋于一致、表面面积趋于最小化，立方体液块在表面张力的作用下将收缩震荡，最终由于流体的粘性作用而稳定成一个规则的球体。该算例的目的在于证明该表面张力算法的正确性。图 3是液块形变模拟过程的部分关键帧截图信息(流体为三维表示，观察方向为水平方向)。

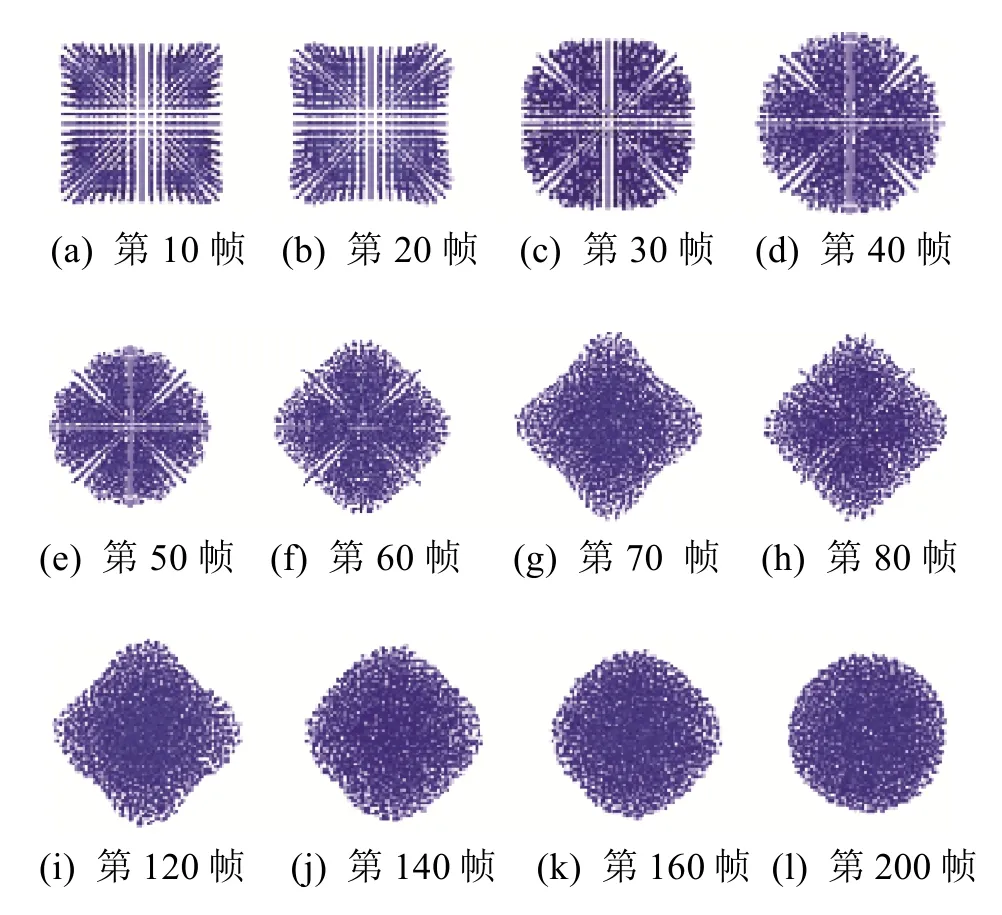
图3 立方体液块形变过程

首先，液块由立方体先是收缩，再迅速形变为一个球体(图 3(a)～(d))；然后，液块由一个球体震荡为一个具有6个尖角的极限状态(图3(e)～(h))；最后，流体由于粘力对动能的耗散作用使得液块形最终稳定在球体状态下(图3(i)～(l))。该结果与文献[7]中采用修正的CSF模型在二维情况下得到的数值模拟结果类似。

4.2 液块碰撞破碎和液滴合并

算例2. 模拟了在体积为1 m×1 m×1 m的固体容器中，体积为0.25 m×0.25 m×0.25 m的液块在重力的作用下下落到与容器底碰撞破碎形成多个液滴，以及液滴在表面张力的作用下合并的过程，并与不施加表面张力情况下做出对比。其中粒子数为810个。图4给出液块在碰撞破碎后施加表面张力与不施加表面张力模拟过程对比(流体为三维表示，观察方向为从容器顶部到底部的垂直方向)。

图4 碰撞破碎过程比较

图 4(a)和(b)自左向右分别是施加表面张力和不施加表面张力的液块自下落开始第60、70、80、90帧的截图信息。从2个模拟过程的对比中可以看出，在施加表面张力的情况下液块在与容器底部碰撞后破碎形成液滴，如图3(a)所示，而不施加表面张力时破碎后成网状失真，并且不能形成分离的圆形液滴，如图3(e)所示。另外，随着流体的运动，施加表面的张力的模拟过程中还伴有液滴间的碰撞合并现象。

液体运动趋于稳定后的比较如图5所示(观察方向为水平方向)，图 5(a)为施加表面张力后形成的一个单独液滴，包含3层SPH粒子，图5(b)则为没有施加表面张力的情况下，流体粒子无法聚拢，从而平铺在容器底部，只有1层SPH粒子。

图5 流体静止状态比较

图6为8幅流体粒子位置截图，显示碰撞破碎产生的多个独立的运动液滴在表面张力的作用下逐渐合并为一个单独的稳定的圆形液滴的模拟过程，该过程发生液体在与容器壁发生碰撞后，多个分散的液滴向容器中央聚拢。

图6 多液滴合并过程

4.3 计算性能对比

为了测试本文方法的计算性能，使用方形液滴自然变化和油滴互溶两个算例，选取运行40帧后添加表面张力的效果与传统的 IIF模型和 CSF模型进行对比，时间为每帧的计算时间(表1)。

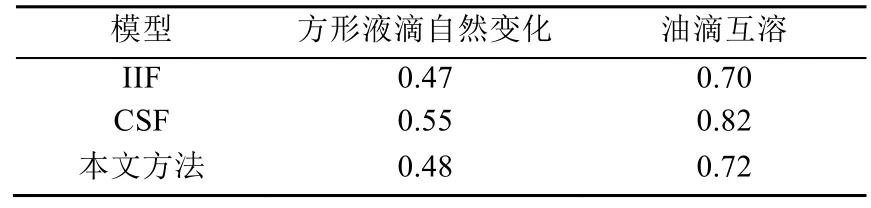
表1 计算速度对比(s)

本文方法由于在计算表面张力修正项过程中直接使用颜色域梯度求解粒子法向，相较于传统CSF模型省去了法向归一化以及相应修正处理过程，在单帧计算速度上略有提高，模拟的场景越复杂，效果越明显。与传统IIF模型相比，本文方法在保证模拟速度的基础上，通过改进聚斥力模型和修正表面张力进一步提高了模拟精度。

5 结 论

本文针对传统的表面张力模拟所采用的IIF模型中存在的缺陷，定义一种最小化表面面积的表面张力修正项，结合基于类L-J势函数的粒子间聚斥力，为SPH方法模拟流体时表面张力的模拟建模。通过模拟立方体液块仅由表面张力驱动时形变为球体的算例验证了本方法的正确性。最后通过比较液块在施加表面张力和不施加情况下碰撞破碎过程的对比以及多液滴合并算例验证了本文方法的有效性。

[1] Solenthaler B, Pajarola R. Predictive-corrective incompressible SPH [J]. Acm Transactions on Graphics, 2009, 28(3): 341-352.

[2] 温婵娟, 欧嘉蔚, 贾金原. GPU通用计算平台上的SPH 流体模拟[J]. 计算机辅助设计与图形学学报, 2010, 22(3): 406-411.

[3] Zhu Y N, Bridson R. Animating sand as a fluid [J]. Acm Transactions on Graphics, 2006, 24(3): 965-972.

[4] Morris J P. Simulating surface tension with smoothed particle hydrodynam ics [J]. International Journal for Numerical Methods in Fluids, 2000, 33: 333-353.

[5] Müller M, Charypar D, Gross M. Particle-based fluid simulation for interactive applications [C]//Preceedings of Symposium on Computer Animation. Aire−La−Ville: Eurographics Association Press, 2003: 154-159.

[6] Hu X Y, Adams N A. A multi-phase SPH method for macroscopic and mesoscopic flow s [J]. Journal of Computational Physics, 2006, 213(2): 844-861.

[7] 强洪夫, 陈福振, 高巍然. 基于 SPH方法的表面张力修正算法及其应用[J]. 计算力学学报, 2011, 28(3): 37-42.

[8] Tartakovsky A, Meakin P. Modeling of surface tension and contact angles with smoothed particle hydrodynam ics [J]. Physical Review E, 2005, 72(2): 026301.

[9] Becker M, Teschner M. Weakly compressible SPH for free surface flows [C]//Proceedings of the 2007 ACM SIGGRAPH/ Eurographics symposium on Computer Animation. Aire−La−Ville: Eurographics Association Press, 2007: 209-217.

[10] Monaghan J J. Smooth particle hydrodynamics [J]. Reports on Progress in Physics, 2005, 68(8): 1703-1759.

[11] Akinci N, Ihmsen M, Akinci G, et al. Versatile rigid-fluid coupling for incompressible SPH [J]. ACM Transactions on Graphics (TOG), 2012, 31(4): 62.

[12] Müller M, Schirm S, Teschner M, et al. Interaction of fluids with deformable solids [J]. Computer Animation and Virtual Worlds, 2004, 15(3/4): 159-171.

[13] He X W, Wang H M, Zhang F J, et al. Robust Simulation of Small-Scale Thin Features in SPH-based Free Surface Flows [EB/OL]. [2015-08-16]. http://life.kunzhou.net/ 2013/SPHsurfacetension.pdf, 2013.

[14] Desbrun M, Gascuel M P. Smoothed particles: a new paradigm for animating highly deformable bodies [M]. Vienna: Springer Vienna, 1996: 61-76.

[15] Kelager M. Lagrangian fluid dynam ics using smoothed particle hydrodynamics [D]. Denmark: University of Copenhagen, 2006.

Surface Tension Simulation for SPH Fluid Based on IIF Model

Dong Lanfang1,2, Zhang Heng1, Chen Junxiong1

(1. Department of Computer Science and Technology, University of Science and Technology of China, Hefei Anhui 230027, China; 2. The State Key Laboratory of Fluid Power Transm ission and Control, Zhejiang University, Hangzhou Zhejiang 310027, China)

Surface tension effect at fluid-air and fluid-solid interfaces should not be ignored when simulating fluid based on smoothed particle hydrodynam ics (SPH) method, it affects the accuracy of the simulation and visual realism. The existing surface tension models such as the continuum surface force (CSF) model and the inter-particle interaction force (IIF) model both have their own flaws. This paper focus on the IIF model which can causes non-physical particle clustering and the irregular shape of fluid surface, and surface tension is modeled by an attraction-repulsion force which is formalized by a Lennard-Jones like potential function, and a SPH tension correction term which based on the normal difference between neighboring particles is introduced to m inim ize the surface area and smooth the surface. Experimental results show that the proposed method can simulate the surface tension effect accurately and stably.

computer graphics; fluid simulation; smoothed particle hydrodynam ics method; surface tension; inter-particle interaction force method

TP 39

10.11996/JG.j.2095-302X.2016030302

A

2095-302X(2016)03-0302-06

2015-09-28；定稿日期：2015-11-13

浙江大学流体动力与机电系统国家重点实验室开放基金项目(GZKF-201318)

董兰芳(1970-)，女，安徽合肥人，副教授，硕士。主要研究方向为科学计算可视化、计算机动画、视频图像智能分析。E-m ial：lfdong@ustc.edu.cn