一种基于空间距离的边绑定方法
2016-11-29杨豪斌
杨豪斌, 周 虹
(深圳大学计算机与软件学院,广东 深圳 518060)
一种基于空间距离的边绑定方法
杨豪斌, 周 虹
(深圳大学计算机与软件学院,广东 深圳 518060)
边绑定方法是近年来信息可视化领域的一个研究热点,解决图可视化中由于边的过多交叉而引起的视觉混乱问题。在现有的边绑定方法中,基于路径构建的算法通常能够在时间和绑定效果上获得较好的结果,其中基于边聚类和骨架构建路径的方法具有良好的数据表达能力。在此基础上,提出一种基于空间距离的边绑定的方法,结合边的空间距离和骨架生成的特点,在实现边绑定功能的同时针对以往基于骨架路径的方法做了进一步的改进。实验结果表明,该方法相比原方法有着更高的时间效率,对数据的细节保留更为合理,消除了原方法存在的绑定过度的问题,简化原方法的计算过程,并避免奇异性问题,更为实用。
边绑定;边聚类;图像骨架算法;图简化;信息可视化
图是信息可视化中一种重要的表现手段,通常以点线图的形式表示。在应对小规模数据的情况下,点线图能够很好地表示数据的结构以及彼此之间的关联。但是随着大数据的发展,可视化所面对的数据规模也在不断膨胀,点线图对于数据的表现能力急剧下降,在众多边交叉的情形下,用户无法辨识图中数据的关联。为了解决这一问题,边绑定便应运而生。边绑定方法在不减少顶点和边的前提下,将图中相似的边捆绑成束,从而减少边的交叉与重叠,达到消除视觉混乱的目的。Telea等[1]所做的用户研究表明边绑定是一种有效的方法,其能够帮助用户更好地分析数据。第一种实用的边绑定方法是Holten[2]提出的,但是只针对具有层次结构的数据。适用于普通图类型数据的边绑定方法是由Cui等[3]首先提出的基于几何的边绑定(geometry-based edge bundling, GBEB),其使用称为控制网格的方法将边绑定到网格路径上。与GBEB类似的基于网格模型的边绑定方法(w inding roads, WR)是Lambert等[4]提出的,WR方法与GBEB的不同之处在于其使用维诺图及四分树来生成网格,而 GBEB则通过手动或自动生成的控制点来产生网格。GBEB和WR模型能够得出较好的绑定结果,但在数据的表现层级上较差,无法呈现复杂程度不同的结果,缺乏数据表现的伸缩性。Holten和Wijk[5]提出的力导向边绑定方法(force-directed edge bundling, FDEB),基于简单的力学模型,有易于实现的优点。姚中华等[6]在力导向模型基础上,从边和群组两个层次对网络图的可视化进行了优化,但总体上基于力导向的算法具有 O(n2)的时间复杂度,在时间效率上表现较差,并且也存在着伸缩性较差的缺点。由Gansner等[7]提出的多层级聚合边绑 定 (multilevel agglomerative edge bundling, MAEB)是一种具有良好伸缩性的方法,其可通过不同的递归次数表现不同的数据层级,但其对图的简化效果较差,在多次递归的情况下依然存在较多的边交叉。Ersoy等[8]提出的基于骨架的边绑定方法(skeleton-based edge bundling, SBEB),其通过生成骨架来构建边的绑定路径。SBEB的计算模型较为复杂,并且在较高迭代次数的情形下存在着绑定过度的问题,但SBEB同时具备了良好的数据表现伸缩性以及对图的简化效果。基于SBEB方法的这些优点,本文主要针对SBEB方法存在的问题加以改进,以期在保留良好的数据表现能力的同时,进一步简化模型的计算流程,提高时间效率。
1 基于骨架的边绑定
给定一个点线图 G=(V,E)(本文假设图G为二维无向图,并且顶点集V和边集E的数据是给定的),SBEB方法的计算流程如图1所示,详细的实现过程参阅文献[7]。
SBEB方法的主要步骤为边聚类、形状构造和边绑定,以及这3个部分的迭代过程。
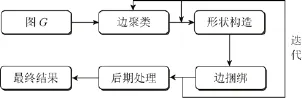
图1 基于骨架的边绑定计算流程
其中边聚类主要是将方向相似,空间距离接近的边分为一类。文献[7]中所提出的聚类算法,在针对直线边的时候能够较有效地对边进行聚类,然而随着迭代次数的增加,聚类个数减少,边变为曲线,其聚类方法的效果变得较差,通常会将本来方向和空间距离差异较大的边分在一类,从而导致数据分析的歧义。形状构造部分将图的布局结果像素化,然后通过图像骨架提取算法[9-11]提取出作为边绑定部分使用的路径。在边绑定上,由于骨架算法本身的特点,在将边上的采样点对应到骨架路径上的时候,可能存在两个对应的骨架路径点,也即边的采样点刚好落到维诺图的路径上(奇异性问题)。SBEB方法通过对角度判断来消除奇异性问题,然而在实现过程,对于角度大小的指定会影响奇异性的判断,出现误判的可能性较大。后期处理部分主要是对绑定结果进行诸如边的平滑等操作,以增强结果的可读性和美观度。迭代次数是影响算法时间效率的关键点,在保证绑定效果的前提下尽可能地减少迭代次数能够使整个算法的时间效率成倍地提高,从而使得算法具有更好的实时性。
针对SBEB存在的边绑定歧义、时间效率和奇异性问题,本文提出了一种基于边的空间距离的新方法。新方法不依赖于通过聚类算法对边进行相似性判断并将其绑定在一起,而是通过判断边的采样点到骨架的距离是否小于一定的阈值作为绑定的依据。在迭代过程中不断将边和骨架的空间位置进行拟合,以使最终的绑定结果最大程度地符合原图中边的分布模式。
2 基于空间距离的边绑定
SBEB方法依靠聚类实现对相似边的绑定,基于空间距离的方法则在绑定的过程中进行判断,当边的采样点与骨架路径的距离小于阈值θ时,才将采样点绑定到骨架路径上,其过程如图2所示。随着迭代过程,边的绑定从外围逐渐深入到内部,直到所有边的采样点与骨架路径的距离 S都小于θ时,完成对边的绑定过程。此过程中,边的分布模式和绑定结果不断地引导骨架路径的生成,最终使得生成的骨架路径很好地拟合了边的空间分布模式,而绑定到骨架上的边便能够很好地表现出原图的分布模式。依据此思想,下面具体说明本文方法主要步骤的实现过程,其计算流程如图2所示。
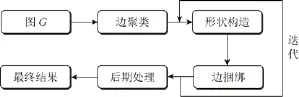
图2 基于空间距离的边绑定算法流程
2.1 边聚类
SBEB方法通过在迭代过程中线性减少层次聚类的划分因子δ来减少聚类个数,以达到最终用户指定的聚类个数,本文方法并不以聚类来判断边的相似性,因此无需在迭代过程中进行聚类,但是为了保证绑定的效果,依然需要对边进行聚类(聚类划分的区域越多,生成的骨架路径也越大,绑定结果中边的扭曲度越小,绑定结果将更符合原图的分布)。在迭代之前进行一次聚类,直接将边划分为用户指定的聚类个数,并且对于聚类的效果不敏感,因此可以充分简化聚类模型。本文方法使用开源的聚类框架[12],并且使用时间复杂度较低的K-means聚类而非原文使用的层次聚类。每条边的特征向量定义为 v=(xs,ys,xe,ye),其中xs、ys为边的始点坐标, xe、 ye为边的终点坐标,同时相似性度量函数定义为欧拉距离函数:

其中,v、w表示边的特征向量,N表示特征向量的维度,即边的采样点数目。对于 K-means的聚类个数 K值,可根据图的复杂程度和用户所需的绑定层级设定。
2.2 边绑定
SBEB方法的边绑定计算公式见式(2),具体可参阅文献[7]中的式(7)。
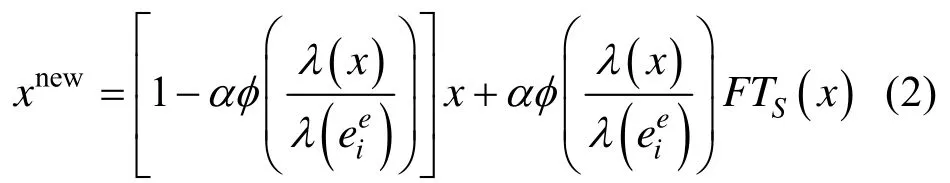
其中,x表示当前的坐标位置, xnew表示新的坐标位置,α用于控制绑定的松紧程度,λ(x)表示从曲线起点到当前坐标位置x的弧长。φ(t)=[2m in(t,1-t)]K(K∈[3,6])控制曲线起始点的位置不变,并且使得越靠近曲线中间部分的采样点移动的越多。 FTS(x)为x的特征变换(feature transform)距离。
SBEB方法主要通过边的平流因子(advection factor)α来控制绑定的聚合速度,α随着迭代次数线性减少,较小的α值使得绑定过程边更好地拟合聚类模式,但需要更多的迭代次数,较大的α值能够加快绑定过程并使得边的绑定更靠紧骨架,但是在简化较为复杂的图时自由度受到限制。
在 SBEB方法中,边的绑定效果与α值有较大关联,原文中将α值根据迭代次数从0.9线性减少到0.2,但实践中发现α值与具体的图布局有很大关系,不同的图布局在采用相同α设置的时候,绑定效果有较大差别,因此实际过程中α需要根据不同的图布局进行设置。为了避免α的设置,基于空间距离的方法不使用α来控制绑定的聚合速度,而是通过边的采样点与骨架路径的距离θ来控制聚合速度。采样点与骨架的距离不会因为不同的图布局而有所变化,其具有统一性,从而防止了SBEB方法中针对α的复杂设定。θ的初始值定义为图布局包围盒的长宽和均值的 0.01,并且随着迭代次数线性增长。θ根据迭代次数线性增长是因为随着迭代次数的增加,边与骨架的拟合程度也越来越高,因此在每次迭代之后适当增加θ值可以有效减少迭代次数,提高整体效率。θ同时也作为采样点是否绑定到骨架路径的依据,如图3(a)所示,只有当前的采样点和对应的骨架点距离 S小于θ时,才进行绑定。θ计算公式见式(3)。
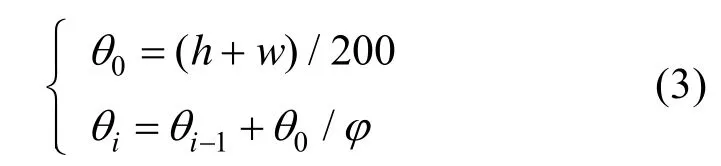
其中,i表示当前迭代次数,0θ表示θ的初始值,h为图布局包围盒的高,w为图布局包围盒的宽。φ为控制聚合速度的因子,φ值越大,迭代过程中iθ越小,边与骨架的拟合度也越高,但是相应增加了迭代次数。经过多次的试验,φ在[4,10]的区间内能得到较好的结果。由于本文方法不使用α值来控制聚合速度,因此可将α设为定值0.9。
2.3 迭代过程
从图1和图2可以看到,迭代过程包含了几个关键的计算步骤,减少迭代次数I能够有效地提高算法的时间效率,在文献[7]中,迭代次数I通常设定在[10,15]之间,以使绑定达到好的结果。本文方法通过θ控制边绑定的聚合速度,同样也影响到迭代次数I上,θ值越大,所需的迭代次数I越少,但是过大的θ值将使边与骨架路径的拟合程度变差。假使θ如式(3)所示的设定,在实际实现过程中迭代次数I在[5,8]之间便能够得到很好的绑定效果,也即本文方法所需的迭代次数能够比SBEB方法减少一半左右,并且对于边的聚类只需进行一次,极大地提高了整体时间效率。图3(b)展示了新方法一次迭代之后的结果。

图3 一次迭代之后的绑定结果(红色部分为骨架路径)
3 奇异性问题
奇异性问题来源于骨架算法的特点,骨架路径上可能存在 2个不同的坐标点对应于一个非骨架路径上的点,而在边绑定过程中,某个边的采样点可能就对应两个骨架路径点,从而导致在绑定过程中曲线边上出现急剧的直线跳跃,使得曲线边不够光滑,如图4(a)中的红色部分所示。
解决奇异性问题可从2个方面进行:①保证在绑定过程中一条边只对应于一条路径,而不以所有路径中与边采样点距离最近的点为基准,此方面确使一条边对应一条路径,不出现一条边在多条路径上跳跃的情况;②即使保证了一条边只对应于一条路径,也可能出现奇异性问题,如图4(a)中的P点。为了解决这个问题,文献[7]提供了一种角度判断的方法,如图4(a)所示,如果角度大于某个设定的阈值β,即判断此处出现奇异性问题,此种解法需要用户指定β的大小,然而在实现过程中固定的β值并不能很好地判断所有的奇异性问题。为了更好地解决此问题,本文改变了边绑定的流程,如图4(b),通过在骨架路径上进行采样,并计算出路径采样点所对应的边的采样点,从而在根本上避免了奇异性问题的产生。新流程的计算过程分为2个步骤:①根据边的端点计算出对应的骨架路径,此路径所对应的是完整路径的一部分,也即子路径;②通过对子路径进行均匀采样,再计算出子路径采样点所对应的边的采样点,从而计算出新的边采样点的坐标。通过对于流程的调整,既解决了奇异性问题,又简化了算法的实现复杂度,增强了稳定性。
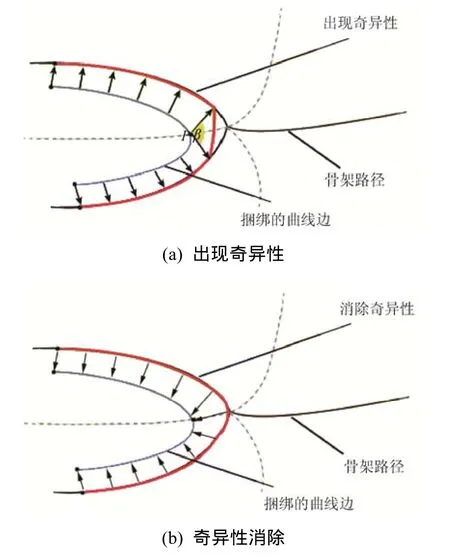
图4 奇异性问题
4 实验结果和分析
实验的硬件设备和软件配置主要为:Intel(R) Core(TM) i3-3110M CPU 2.40 GHz,内存为8 GB,显卡为 NVIDIA GeForce GT 630 M,64-bit Windows 7 Professional 操作系统,Visual Studio 2010开发平台,C++与OpenGL。
本文的数据来源于文献[3-5]和文献[7-8],分别为美国西北航空线路图、美国迁移数据图和扑克玩家关系图。实验的统计数据如表 1所示。从表 1的实验结果可以看出,由于有效地简化了计算模型和减少了迭代次数,本文方法在时间效率上有了较大的提升。
从图 5的结果对比来看,本文方法在实现了图简化的同时保留了更多的数据细节。以西北航空图为例,对比图5(d)、(f)、(h),明显看出图5(h)较好地保留了原图的局部走向,图5(f)在中间部分和右半部分明显出现了过度绑定,导致数据出现了较大的“失真”。从迁移图的比较来看,两种方法效果差别不是很大,但是依然能够看出图5(g)在最右部分出现了较明显的过度绑定,而本文方法则较好地保留了原图的基本走向。本文方法相比较于 SBEB方法更好地解决了由于数据规模引起的视觉混乱和数据表达之间的矛盾。

表1 数据集的实验结果
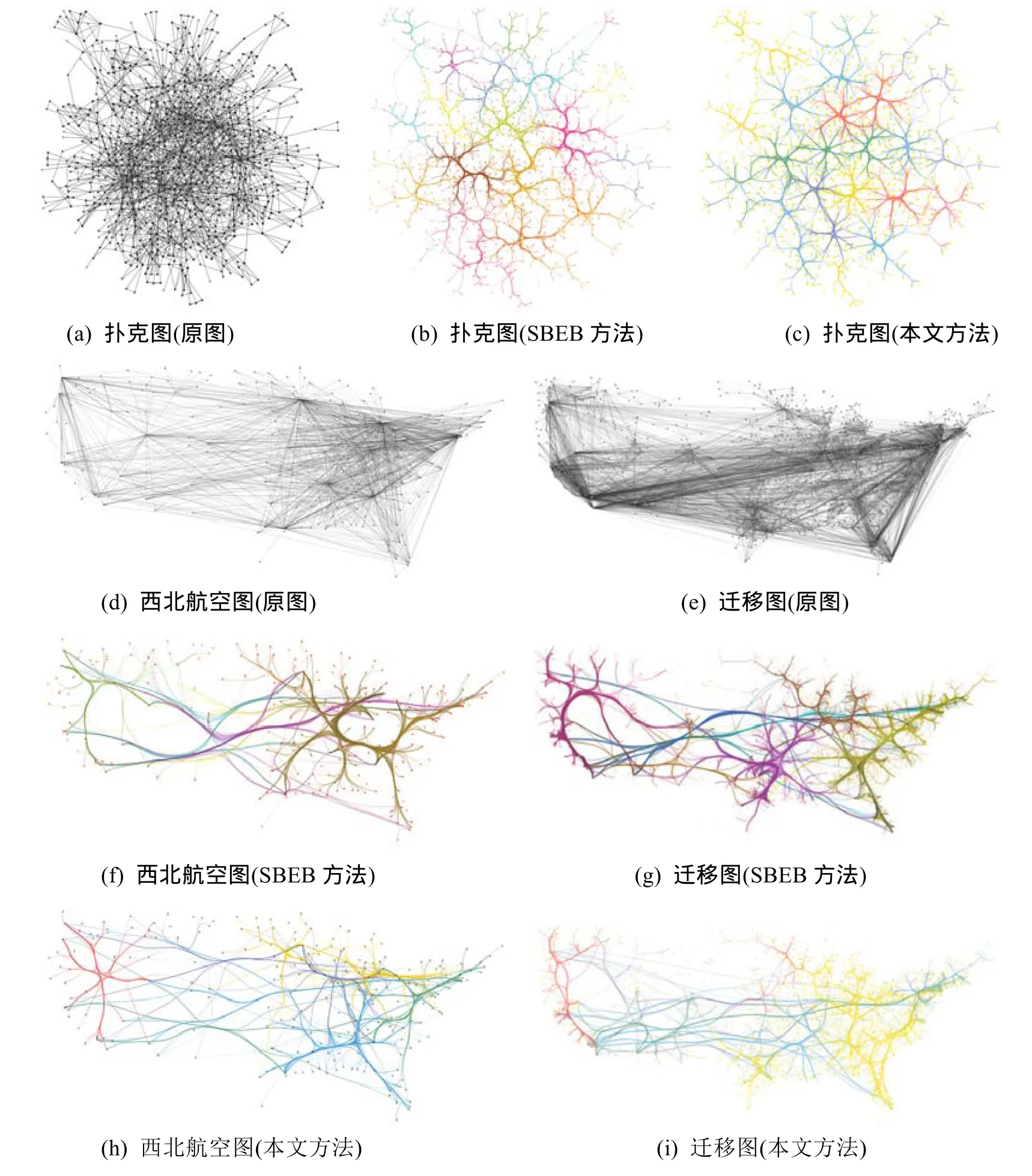
图5 SBEB方法与本文方法结果对比
5 结 束 语
本文主要基于SBEB方法中骨架路径的思想,并从图布局的空间距离考虑,提出了一种新的边绑定方法。同时针对 SBEB方法出现的奇异性问题,对边的绑定流程进行了调整,避免了对参数的设定,有效地简化算法的实现复杂度。本文方法也存在一些不足,为了减少迭代次数,随着迭代次数的增加,θ呈线性增长,会在一定程度上影响边与骨架的拟合程度。从绑定结果上,在相同的聚类数目下,本文方法能够有效地对边进行绑定,并且保留更多的细节,在减轻图的视觉混乱和数据的呈现上做到了较好的平衡,但是从美学上,本文方法的表现结果要比SBEB稍差。总体上来说,基于空间距离的方法有着更高的时间效率和更低的实现难度,是一种有效的方法。
[1] Telea A, Ersoy O, Hoogendorp H, et al. Comparison of nodelLink and hierarchical edge bundling layouts: a user study [C/OL]//Dagstuhl Seminar Proceedings 09211: Visualization and Monitoring of Network Traffic. [2015-04-15]. http://drops.dagstuhl.de/protals/index.php? semnr=09211.
[2] Holten D. Hierarchical edge bundles: visualization of adjacency relations in hierarchical data [J]. IEEE Transactions on Visualization and Computer Graphics, 2006, 12(5): 741-748.
[3] Cui W W, Zhou H, Qu H M, et al. Geometry-based edge clustering for graph visualization [J]. IEEE Transactions on Visualization and Computer Graphics, 2008, 14(6): 1277-1284.
[4] Lambert A, Bourqui R, Auber D. Winding roads: routing edges into bundles [J]. Computer Graphics Forum, 2010, 29(3): 853-862.
[5] Holten D, Wijk J J V. Force-directed edge bundling for graph visualization [J]. Computer Graphics Forum, 2009, 28(3): 983-990.
[6] 姚中华, 吴玲达, 宋汉辰. 网络图中边集束优化问题[J]. 北京航空航天大学学报, 2015, 41(5): 871-878.
[7] Gansner E R, Hu Y, North S, et al. Multilevel agglomerative edge bundling for visualizing large graphs [C]//In Proceedings of IEEE Pacific Visualization Symposium. Washington: IEEE Computer Society, 2011: 187-194.
[8] Ersoy O, Hurter C, Paulovich F V, et al. Skeleton-based edge bundling for graph visualization [J]. IEEE Transactions on Visualization and Computer Graphics, 2011, 17(12): 2364-2373.
[9] Telea A, Van Wijk J J. An augmented fast marching method for computing skeletons and centerlines [C]//In Proceedings of the symposium on Data Visualisation 2002. Aire−La−Ville: Eurographics Association, 2002: 251-259.
[10] 赵春江, 施文康, 邓 勇. 具有鲁棒性的图像骨架提取方法[J]. 计算机应用, 2005, 6(6): 1305-1306.
[11] 杨志平, 齐清文, 黄仁涛. 数学形态学在空间格局图像骨架提取中的应用[J]. 地球信息科学, 2003, 2(2): 79-83.
[12] Hoon M D, Imoto S, Nolan J, et al. Open source clustering software [J]. Bioinformatics, 2004, 20(9): 1453-1454.
A Distance-Based Edge-Bundling Method
Yang Haobin, Zhou Hong
(College of Computer Science & Software Engineering, Shenzhen University, Shenzhen Guangdong 518060, China)
Edge bundling has become a research hotspot in the field of information visualization. The edge-bundling methods address the visual clutter problem caused by extensive edge crossings in graphs. Among the recent edge-bundling methods, the algorithms which are based on the path construction are generally efficient and have good bundling results, the algorithms which are based on edge clustering and the skeleton construction can effectively reveal underlying patterns. Based on these works, a distance-based edge-bundling method is presented, with the features of space distances and skeletons, which can improve the edge-bundling results generated by the skeleton-based edge-bundling method. The experiment results demonstrate that the distance-based method is efficient and effective in pattern revealing, so that this method can avoid the over bundling problem of the previous one. In summary, this method is a practical one that can simplify the computing process and avoid the singularity problem.
edge bundling; edge clustering; skeleton-based algorithm; graph visualization; information visualization
TP 301.6
10.11996/JG.j.2095-302X.2016030296
A
2095-302X(2016)03-0296-06
2015-09-28;定稿日期:2015-12-01
国家自然科学基金青年科学基金项目(61103055)
杨豪斌(1988–),男,广东普宁人,硕士研究生。主要研究方向为信息可视化。E-mail:haobinyang1988@163.com
周 虹(1982–),女,湖南长沙人,讲师,博士。主要研究方向为信息可视化和可视分析。E-mail:hzhou@szu.edu.cn
