控制柜关键因素热布局优化研究

左晓刚，崔国民

（上海理工大学 新能源科学与工程研究所，上海 200093）

控制柜关键因素热布局优化研究

左晓刚，崔国民

（上海理工大学 新能源科学与工程研究所，上海 200093）

随着电子设备向高性能、微型化、集成化的趋势发展，控制柜的散热能力不仅影响电子元件的性能和使用寿命，更对系统稳定性有着重要意义。以控制柜内整体区域平均温度作为优化目标，根据L64(88)正交表的模拟值拟合得到多次回归方程，并求解方程得到最优解。结果表明：采用非线性拟合与数值模型符合性更高，二次回归方程拟合效果最好。根据二次回归方程得到控制柜热设计最佳布局，为提高电子产品热可靠性设计提供了借鉴意义。

平均温度；正交试验；热布局优化；可靠性

0　引言

随着电子技术日新月异的发展，作为信息革命的载体——电子设备也不断向高性能、微型化、集成化的趋势发展[1,2]。如今，电子元件的热流密度已经达到104～105W/m2[3]。一般来说，电子元件的绝大部分电损耗转化为热量，而产生的热量将急剧提升电子装置的结点温度，从而导致元件不能正常工作、损坏甚至烧毁。因此，电子元件的散热问题成为电子工业技术发展的当务之急。资料表明，单个半导体元件的温度升高10℃，一些电子系统的可靠性甚至降低50%[4]。另据资料表明，55%的电子设备失效是由温度过高引起的[5]。电子设备在运行过程中，由于功率损失元件温度不断上升，同时电子设备周围的环境温度也会影响元件温度，元件在环境温度每升高10℃失效率增大一倍以上，被称为10℃法则[6]。在电子设备运行过程中，电子元件的热量不能及时排出极大的影响了电路的可靠性和寿命，因而热设计的好坏将直接影响到电子设备的性能和使用寿命。

国内外学者对布局优化主要集中于印制电路板[7～9]，少有对系统复杂、规模庞大的电子设备有所研究。控制柜具有大功率、高可靠性、系统复杂、规模庞大的特性，目前采用CFD（Computational Fluid Dynamic）方法是目前较为实用的热设计方法之一，对其进行布局优化时所设定优化目标很难得到与设计变量的显式函数式，控制柜的优化不仅受到几何条件的限制，还受到工业实际应用等限制。控制柜内环境温度的降低对内部元件的可靠性增加有着极大的提升，因而本文采用整体区域的平均温度作为环境温度的近似并对其进行优化。控制柜这样庞大而又复杂的模型每进行一次三维数值模拟都要耗费大量的计算机时间，而在优化设计过程中需要反复计算目标函数值，如果每次都要调用模拟软件，那么超大的计算量将使优化工作无法进行。作为控制柜的优化的很重要的一个问题就是怎样在计算时间和计算容量允许的前提下将模拟分析用于优化设计过程。本文通过调用有限次模拟软件，求得设计目标与设计变量的近似函数，对近似函数进行优化，将近似函数的最优解返回原模型中进行验证。近似函数具有固定形式，能够方便得到目标函数的最优解，可以大大提高优化效率。

本文在不改变散热条件的情况下，利用基于CFD技术的ANSYS软件对控制柜进行热模拟，将平均温度作为优化目标，通过改变控制柜内部关键因素位置，以L64(88)型正交试验为基础，拟合多次回归方程并求解其最优解，并验证选择最佳回归方程模型，确定控制柜布局方式，为控制柜热设计提供了一定的参考价值。

1　模型建立

1.1物理模型

控制柜内含有大量的电子元件，同时柜内布线复杂。为了实现对控制柜的传热数值模拟，需要对控制柜内模型简化处理，将电线的发热量折合到电子元件中并将元件的几何外形简化，元件各向同性均匀导热，其主要电子元件发热量如表1所示。控制柜几何尺寸长宽高1100mm×390mm×1400mm，壁面设置有入风口（inlet-left、inlet-right）和出风口（outlet-left、outletright），关键电子元件及通风口位置图如图1所示。

表1　电子元件名称与发热量

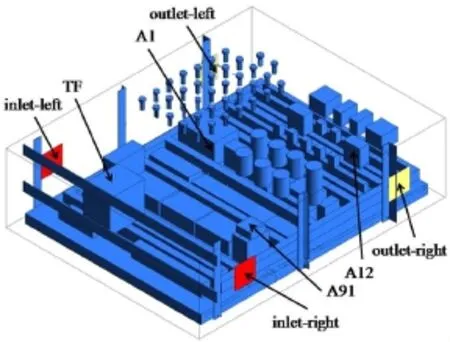
图1　控制柜立体图

1.2数值模拟模型

控制柜采用空气强迫对流对电子元件进行冷却，入风口风速取为3m/s，出风口为压力出口，其压力为101325Pa，环境温度30℃，过程为稳态。计算软件为ANSYS软件的Icepak模块，控制方程采用有限体积法离散，应用SIMPLE法处理压力速度耦合，对流项采用一阶迎风格式离散，扩散项采用中心差分格式，湍流模型采用k-ε模型。根据文献[10]，电子元件的内部温度及外表面温度一般均不超过150℃，而环境温度一般为20℃～40℃。因此，控制柜模型不考虑辐射换热，其平均温度是空气流经区域的节点温度平均值，节点数目在60000左右。

2　控制柜正交回归设计及优化

2.1试验因素和试验方案的确定

正交试验设计又被称为多因素优选设计，是一种合理科学安排试验次数的数理统计方法。采用正交试验可以尽可能地减少试验次数，以较小的试验数据规模得到有效的结论。

控制柜初始布局下的平均温度为33.46℃。根据控制柜电子元件发热量和实际工程应用，选择如图1所示电子元件A1、TF、A91、A12及入风口inlet-left、inletright和出风口outlet-left、outlet-right共8个变量作为正交试验的因素，试验水平选为8。各因素的原始位置尺寸作为基本尺寸，其尺寸变化范围限定为因素的最大最小值，每个因素根据水平数和尺寸变化幅度选择水平值。根据统计分析软件生成正交表，不考虑因素之间的交互作用并设置空列，采用L64(88)型正交表，其因素水平值如表2所示。

表2　正交试验设计水平

根据正交表生成的64种设计变量组合依次模拟计算得到64组平均温度值，其结果如表3所示。

2.2回归方程的建立及优化

根据L64(88)型正交表的模拟结果表3建立平均温度与所设计因素之间的近似函数，由于控制柜系统的复杂性，其方程形式可确定为非线性形式。为了尽量得到较好的回归方程，采用方程(1)形式进行回归拟合，其中y为平均温度，c为常数项，xji为设计因素，aij为xji对应的系数。模拟值与回归方程值误差如图2所示，误差变化趋势相同并且在均在±4%以内说明拟合方程是准确的，非线性拟合较线性拟合误差更小说明非线性拟合符合性更高，在给定的因素变化范围内通过穷举法求解对应的方程得到其最优解及因素取值，将最优解对应的因素值代入模拟软件中进行再次求解得到模拟值以验证方程结果如表4所示。

表3　模拟结果

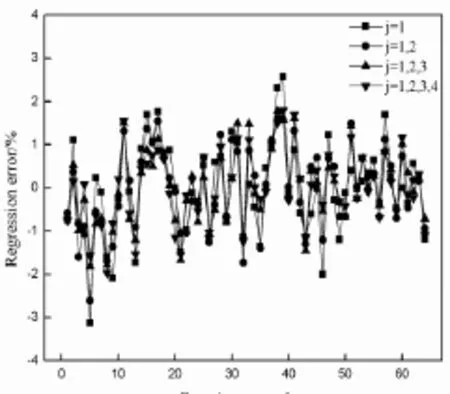
图2　回归方程误差

实际问题中，变量之间的关系式不是确切的，因素次方越多越高其与实际的符合性越好，但在实际求解过程中由于计算模拟的误差，拟合回归关系的误差以及优化的误差，因素次方不是越高越好。如表4所示所有回归方程模拟值与初始布局值相比至少下降1℃说明回归方程是有效的，但随着最优解逐步降低模拟解不减反增，说明回归方程求解误差逐步增大使其产生了偏差，二次方回归方程对应的模拟解最为符合，其形式如方程(2)所示。

表4　最优解和模拟解对比

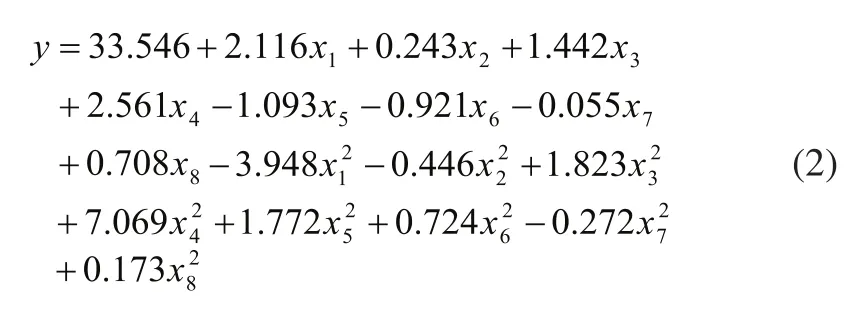
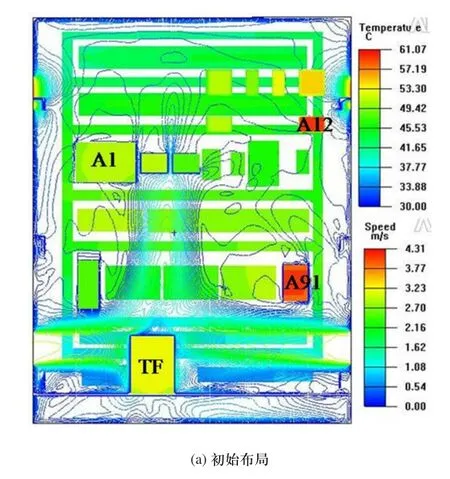
图2显示了初始布局及二次方回归方程模拟解元件温度分布与速度等高线图。由图2可知：图(a)显示控制柜下方及中间左右区域均有速度死区，根据方程(2)最优解将通风口及元件移动到图(b)位置，入风口位置下移使得速度死区基本消失，空气流经了更多的内部区域，其整体散热得到了一定程度的改善，同时所选元件A12、A1、A91的温度也得到了改善。

【】【】

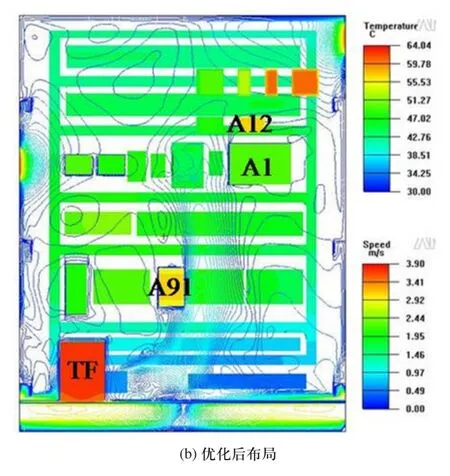
图3　温度分布与速度等高线图对比图

3　结论

通过对控制柜的正交试验，改变因素位置，借助统计分析软件生成的正交表对控制柜进行了数值模拟，根据模拟值拟合回归方程并优化，得到了以下结论：

1）以空气流经区域节点温度平均值作为平均温度，L64(88)正交表模拟值拟合回归方程可以更加精确地描述平均温度与设计因素的关系。

2）采用非线性拟合方式较线性拟合与实际的符合性更高，但由于模拟数据、回归方程和优化求解过程误差的存在，二次方回归方程拟合效果最好，根据二次方回归方程得到控制柜热设计最佳布局，为提高电子产品热可靠性设计提供了借鉴意义。

[1] Jian-Hui Z,Chun-Xin Y. Design and simulation of the CPU fan and heat sinks[J].Components and Packaging Technologies, IEEE Transactions on,2008,31(4):890-903.

[2] 刘东.高热流密度微结构散热器换热特性的研究[D].中国科学技术大学,2011.

[3] 郝俊娇,潘日,周刚,等.高热流密度电子元件中热管散热技术的进展[J].化工进展,2015,34(05):1220-1224+1231.

[4] Nelson L,Sekhon K, Fritz J. Direct heat pipe cooling of semiconductor devices[A].3rd International Heat Pipe Conference[C]. 1978:373-376.

[5] 刘绪磊,周德俭,黄春跃,等.基于正交试验的板级电路模块热分析[J].电子元件与材料,2009,28(5):43-46.

[6] 齐永强,何雅玲,张伟,等.电子设备热设计的初步研究[J].现代电子技术,2003(01):73-76+79.

[7] Suwa T, Hadim H. Multidisciplinary placement optimization of heat generating electronic components on a printed circuit board in an enclosure[J].Components and Packaging Technologies, IEEE Transactions on,2007,30(3):402-410.

[8] 梁颖,黄春跃,阎德劲,等.基于热叠加模型的叠层3d多芯片组件芯片热布局优化研究[J].电子学报,2009,37(11):2520-2524.

[9] 王乃龙,戴宏宇,周润德.用模拟退火算法实现集成电路热布局优化[J].半导体学报,2003,24(04):427-432.

[10] 孙志坚.电子器件回路型热管散热器的数值模拟与试验研究[D].杭州:浙江大学,2007.

Study on thermal layout optimization of control cabinet important factor

ZUO Xiao-gang, CUI Guo-min

TP391.9

A

1009-0134(2016)02-0097-04

2015-10-26

国家自然科学基金资助项目（51176125）；沪江基金研究基地专项（D14001）

左晓刚（1990 -），男，内蒙古包头人，硕士研究生，研究方向为强化传热及高效换热器。