基于前馈补偿的直升机控制律设计与仿真

刘宇亮+张琳+朱亚芬

摘要： 以某型运输直升机为研究对象， 根据飞行品质规范ADS-33E的要求， 在增稳控制的基础上， 设计前馈补偿控制律， 以改善系统的操纵性。 通过拟合不同设计节点的前馈控制参数， 实现包线内的调参控制律。 对所设计的系统进行仿真试验验证， 结果表明采用上述控制方案可取得良好的控制效果， 证明了该方法的可行性和有效性。

关键词： 直升机； 飞行品质规范； 前馈补偿； 控制律； 系统仿真

中图分类号： V249.122+.4 文献标识码： A 文章编号： 1673-5048（2016）04-0030-06

Abstract： Taking a transport helicopter as the research subject， based on stability augmentation control， feedforward compensation control law is designed to improve the control system according to the flying qualities specification of ADS-33E. By fitting the feedforward control parameters of different flight nodes， parameter adjusting control law in the full scale flight envelop can be realized. The designed system is simulated and tested， and the results indicate that satisfied control effect is obtained by adopting the proposed control method， which proves the feasibility and effectiveness of the method.

Key words： helicopter； flying qualities specification； feedforward compensation； control law； system simulation

0引言

由于直升机的稳定性较差， 只靠飞行员操纵来完成复杂、 精确的飞行是非常困难的， 故需要通过加入飞行控制系统来改善其飞行品质[1]。 基于三轴稳定控制的增稳控制系统虽然能够有效提高飞机的稳定性， 但是会导致系统响应的速度变慢、 幅值变小， 从而造成快捷性、 操纵功效等性能指标等级不高。 针对上述问题， 可以通过在增稳控制回路前面增加一个前馈电气通道的方式来解决问题， 这就是控制增稳系统， 该系统能够在兼顾直升机稳定性的同时提高操纵功效等性能。 此外， 直升机各通道之间耦合影响严重， 通过前馈补偿方式实现交联解耦控制， 可以有效提高直升机的操纵品质。 所以， 直升机控制增稳系统的设计与实现具有重要的理论意义和实际意义。

1飞行品质规范ADS-33E的要求

针对直升机操纵性能的优劣， 美国军用直升机飞行品质规范ADS-33E[2-3]有明确规定。

1.1对姿态响应的要求

飞行品质规范ADS-33E分别针对飞机的小幅/高频、 小幅/中频、 中幅/中低频和大幅姿态变化的响应规定了相应的指标要求， 即带宽及相位滞后、 阻尼比、 快捷性和操纵功效。 对于俯仰姿态变化， 5°以下为小幅， 30°以上为大幅； 滚转姿态的划分界限为10°和60°； 对航向角没有明确数据。 飞行速度V≤23 m/s时为低速和悬停状态； V>23 m/s时为前飞状态。

带宽及相位滞后指标规定了频域要求， 保证快速操纵时直升机具有良好的跟随性和灵敏度。 设从驾驶员输入量到相应姿态角输出量的传递函数为G（s）， 相关定义在其波特图中， 如图1所示。

图1中出现了相位带宽和增益带宽， 其中相位滞后135°的频率定义为相位带宽， 在幅频曲线上留出6 dB的余量所对应的频率为增益带宽。 由于研究对象的响应类型为姿态指令姿态保持响应类型（ACAH）， 带宽ωBW=ωBWphase。 延迟时间τp用以表示系统的相位滞后， τp越小说明相位曲线随频率下降越慢， 直升机的驾驶品质越好。

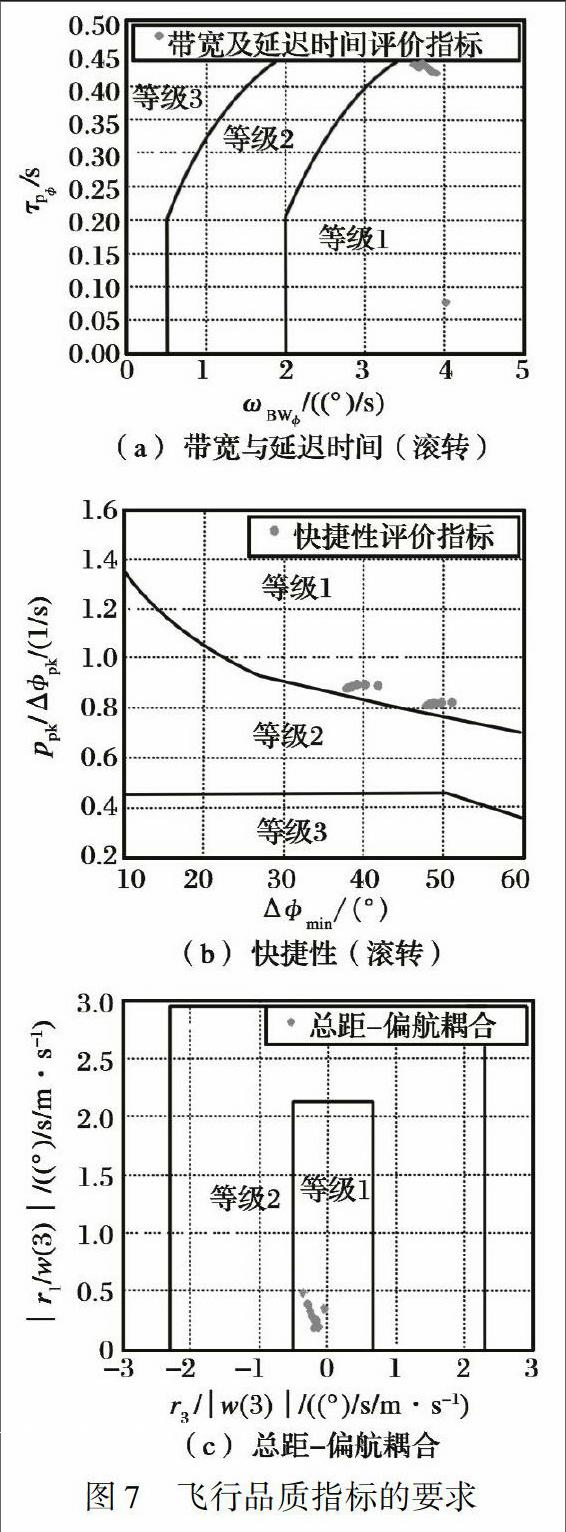
飞行品质指标的要求如图2所示。 为了表征带宽和延迟时间与飞行品质的关系， ADS-33E在带宽-延迟时间二维平面内定义了不同的区域， 以区别飞行品质的高低； 而且按照不同的任务科目基元、 环境感知度和控制通道规定了不同的标准。 由于本文的研究对象是运输型直升机， 所以选择除空战外的MTE且UCE=1， 以滚转通道为例， 带宽与延迟时间的品质指标要求如图2（a）所示。

对于直升机的动稳定性， 飞行品质规范对系统的阻尼比、 自然频率也做出了具体的规定。 以滚转通道为例， 阻尼比和自然频率的限制如图2（b）所示。

针对飞机改变姿态的快慢， 对操作响应的快捷性做出要求， 即角速度峰值对姿态改变量之比要足够大。 以滚转通道为例， 快捷性指标的要求如图2（c）所示； 其中 Δpk和Δmin分别为滚转角阶跃响应的峰值和最小值， ppk为滚转角速度的最大值。

大机动飞行时， 直升机的响应要具备足够大的姿态变化（对于姿态指令/姿态保持响应型）或足够大的角速度（对于速率响应型）， 品质规范规定了其最低限。 以滚转通道为例， 针对姿态指令响应类型且有限机动的飞机， 1级品质等级的要求为在飞机悬停与低速飞行时， 滚转角至少达到±15°； 在前飞时， 滚转角至少达到±25°。

1.2对总距操纵响应的要求

航空兵器2016年第4期刘宇亮等： 基于前馈补偿的直升机控制律设计与仿真飞行品质规范对总距操纵响应的时域要求为驾驶员对总距杆施加阶跃操纵后， 法向速度应在5 s之内具有大致为一阶的形状。 这是为了保证总距突变后初期的法向速度应直线变化， 便于驾驶员精确控制升降和高度。 此外， 品质规范规定了总距操纵的操纵功效， 即操纵总距杆快速偏离配平位置后的1.5 s内， 产生的法向速度至少达到0.81 m/s （等级1）、 0.28 m/s（等级2）、 0.20 m/s（等级3）。

1.3对轴间耦合的要求

式中： A∈R9×9为状态矩阵， B∈R9×4为控制矩阵， A， B中的参数随飞行高度和速度的变化而变化； C∈R9×9为输出矩阵（取为单位阵）； X=[u v w θ ψ q p r]为状态向量， 其中， u， v， w分别为前向、 横向和法向速度； θ， ， ψ分别为俯仰角、 滚转角和航向角； q， p， r分别为直升机绕机体OX， OY， OZ轴的角速度； U=[δeδaδrδc]为输入向量， 各分量依次为纵向周期变距、 横向周期变距、 尾桨桨距和总距。

直升机模型中的参数随飞行高度和速度而变化， 故选取不同高度和速度下的14个飞行状态点作为研究对象， 如表1所示。

2.2增稳控制系统

为提高直升机的静稳定性， 便于驾驶员操纵， 通常采用加入增稳控制系统的方法。 本飞机的增稳控制包括三轴稳定和高度稳定两部分。[4]

三轴稳定控制系统设计的目的是实现直升机姿态角稳定。 在俯仰、 倾斜、 航向三通道分别引入各通道姿态角和姿态角速度信号， 实现比例加测速反馈控制[5]， 并设计满足要求的控制参数。 高度通道则引入高度传感器和法向加速度计信号， 设计PID控制器， 保证飞机高度稳定并能跟踪给定的高度指令[6]。 在增稳系统基础上设计前馈控制器， 提高飞机的操纵性能。

3增稳控制系统性能的检验

依据飞行品质的要求， 通过仿真试验评价加入增稳系统后飞机的操纵性能， 为前馈控制器的设计提供依据。

3.1对姿态响应的检验

取飞行状态点4（速度V=41 m/s、 高度H=100 m）， 以滚转通道为例进行检验。

使用MATLAB中的linmod（）函数， 求出仿真模型中驾驶杆横向位移量到滚转角的传递函数； 并根据飞行品质规范中的规定， 计算得出带宽ωBW=5和延迟时间τp=0.05。 可以看出， 飞机滚转通道的带宽与延迟时间达到1级品质指标的要求， 表明前期所设计的三轴稳定控制律达到了较理想的带宽和延迟时间指标要求。

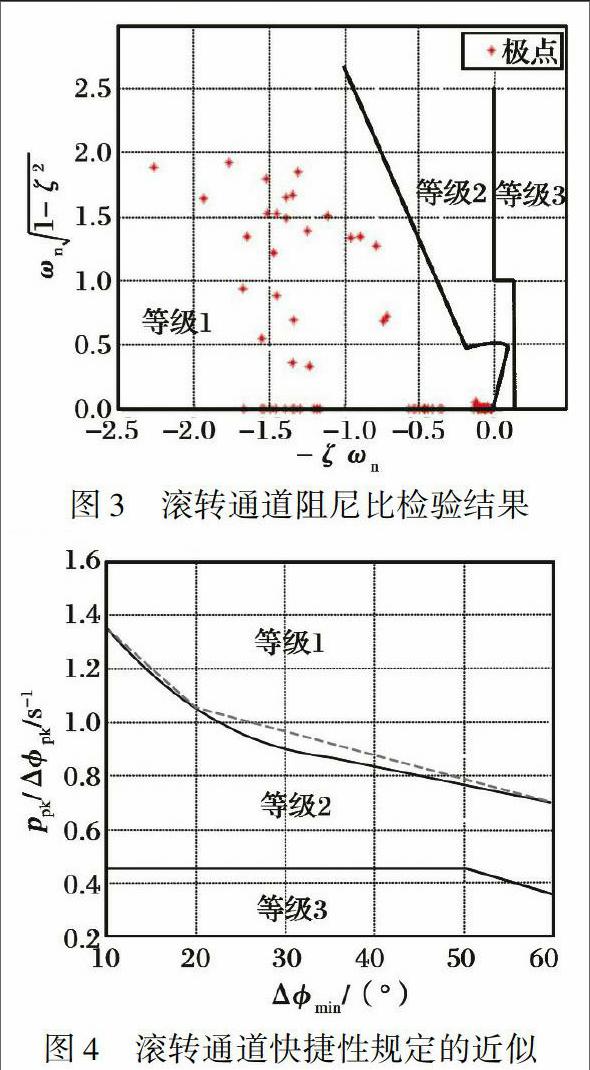
求出驾驶杆位移量到滚转角传递函数的极点， 根据极点在复平面上的位置， 确定阻尼比的品质等级， 见图3所示。

由图3可以看出， 滚转通道传递函数的极点全部落在1级品质要求的区域内， 表明加入三轴稳定控制律的飞机具有满意的阻尼特性。

给直升机的滚转通道加入幅值为20的阶跃信号， 根据仿真试验得出ppk/Δpk=1.07， 由于阶跃响应没有超调量， 故Δpk=Δmin=12.12， 快捷性和操纵功效都位于2级指标范围内。 可见加入增稳控制系统后， 飞机的快捷性和操纵功效有待改进。

3.2对总距操纵响应的检验

在飞机的高度通道加入幅值为20的阶跃信号， 根据仿真结果可知， 14个飞行状态点下飞机的法向速度变化基本为一阶形状， 1.5 s末的法向速度最小为0.89 m/s， 都能达到1级品质的要求。

3.3对轴间耦合的检验

取飞行状态点4， 首先在高度通道加入幅值为10的阶跃输入， 根据仿真结果得出|r1/w（3）|=0.71， r3/|w（3）|=-0.63， 可知该耦合效应达到等级2。 同理可知， 俯仰-滚转通道也存在一定的耦合效应， 有必要针对上述2个通道设计解耦控制器。

4控制律设计

由第3节中的仿真验证及分析可知， 飞机滚转通道的带宽与延迟时间、 阻尼比和总距操纵品质指标都达到1级品质； 快捷性、 操纵功效和轴间耦合品质指标有待提高。 本节中， 使用按输入补偿的前馈校正方法， 在飞机原有机械通道的基础上加入前馈电气通道， 提高飞机的快捷性和操纵功效； 使用按扰动补偿的前馈校正方法， 在飞机的俯仰和高度通道中引出解耦通道， 抑制轴间耦合。

4.1增控通道的设计

根据传递函数G（s）的频域特性可知， 低频时幅值大且相位滞后小， 高频时相反， 这样的特性正好体现了飞行品质规定对不同姿态变化响应的具体要求。

4.1.1参数k的设计

（1） 根据快捷性要求设计参数

快捷性1级品质的要求如图4所示， 为了方便设计， 把划分等级的曲线近似为分段直线， 如图4中虚线所示。

分别在原有机械通道和新加入的前馈电气通道输入幅值为20的阶跃信号， 通过仿真试验得出： 经过机械通道， 飞机滚转角响应的最大值为pk1、 最小值为min1， 最大滚转角速度为ppk1； 当前馈通道的增益为1时， 滚转角的最大值为pk2、 最小值为min2， 最大滚转角速度为ppk2。

式中： k0， k和T均为正数， 由于k0Tk0+k

4.2解耦通道的设计

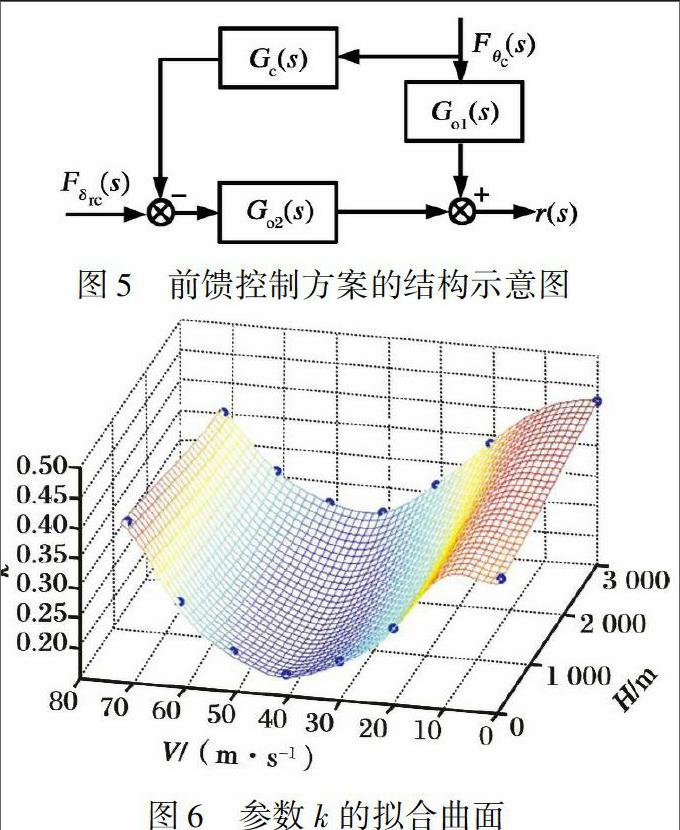
解耦控制系统的工作原理为当驾驶员操纵飞机引起期望之外的响应时， 可以把操纵量看作期望外响应的干扰输入， 设计该操纵量到期望外响应对应操纵输入的前馈通道， 用来抵消该操纵量引起的期望外响应。 以高度到航向通道的解耦控制器设计为例， 相应方案的示意图如图5所示。

取飞行状态点4， 针对增稳后的飞机模型， 使用MATLAB中的linmod（）函数， 计算出传递函数Go1（s）和Go2（s）， 经过化简后， 可得高度到航向通道解耦控制器的传递函数Gc（s）。

经过仿真可得， 加入解耦控制器后， 飞行员对总距杆输入相同幅度的阶跃量时， |r1/w（3）|的值从0.71减小为0.21； r3/|w（3）|的值从-0.63变为-0.14， 且品质等级达到1级。 由此可得， 解耦控制器Gc（s）可以有效抑制高度到航向通道的交联耦合。 同理， 可以设计出俯仰到滚转的解耦控制器。

4.3全包线控制律实现

针对不同飞行状态点（具体描述见表1）， 分别设计控制器； 并以其参数为样本， 按照严格径向基神经网络的算法[7-8]， 使用newrbe（）函数分别得到前馈控制器和解耦控制器传递函数参数的神经网络拟合曲面（其中， 解耦控制器可以整理为尾1标准型， 即分子、 分母各次项系数和开环增益k）。

以开环增益k为例， 其拟合曲面如图6所示。 可以看出拟合曲面连续、 光滑， 较好地反映了k在包线内的变化趋势。 相比之下， 速度变化对k的影响较大， 高度变化对k的影响较小， 客观反映了速度对直升机特性影响较大的事实。

5仿真验证

以滚转通道为例检验飞机姿态响应的品质等级。 分别对表1中所有飞行状态点对应的模型进行仿真， 验证加入控制增稳系统后直升机的动态响应， 以及各飞行品质指标所能达到的等级。 由于加入前馈环节不改变控制系统的极点， 故不再验证系统的阻尼比。 由于高度通道没有加入前馈增控环节， 故总距的响应与3.2节中相同， 不再验证。

加入前馈增控通道和解耦控制器后， 系统的仿真框图见图7。

飞行品质指标的要求如图7所示。

由图7（a）可以看出， 飞机的带宽与延迟时间虽然能够达到1级品质， 但是， 加入前馈通道后带宽变窄， 延迟时间变长。 对比飞行状态4对应的数据发现带宽ωBW从5变为3.68； 延迟时间τp从0.05变为0.44。 图7（b）反映出快捷性指标可以达到1级品质， 飞行状态点5对应的具体数据为ppk/Δpk=0.89， Δpk=Δmin=39.26， 同时Δmin>25说明操纵功效满足了1级品质的要求。 图7（c）给出了总距到航向通道轴间耦合的检验结果， 可以看出在全部飞行状态点处， 该指标都满足1级品质指标的要求。

6结论

针对已实现增稳控制的直升机模型， 本文按照飞行品质规范ADS-33E中的有关规定， 评价了品质指标的等级。 由于飞机的快捷性和操纵功效没有达到1级品质， 故基于按输入补偿的前馈控制原理， 设计出增控环节； 针对飞机轴间耦合严重、 品质等级指标较低的实际情况， 基于按扰动补偿的前馈控制原理， 设计出解耦控制器。 经过仿真验证和数据对比可以看出， 加入增控环节和解耦控制器后， 飞机的快捷性、 操纵功效显著提高， 轴间耦合明显减轻， 所考核检查的指标均可以达到1级标准， 仿真结果证明所采用的控制增稳方法可以达到较好的控制效果。

参考文献：

[1] 杨一栋. 直升机飞行控制[M].北京： 国防工业出版社， 2007： 25-30.

[2] ADS33E， Handling Qualities Requirements for Military Rotorcrafts[S].United States Army Aviation and Troop Command， 1996.

[3] 荣袅录.直升机飞行品质设计方法研究[D]. 南京： 南京航空航天大学， 2007.

[4] 赵鹏轩. 直升机过渡悬停及缆位缆高控制律设计与仿真[D].西安： 西北工业大学， 2011.

[5] 凌琼. 直升机控制律设计[D]. 西安： 西北工业大学， 2008.

[6] 韩旭， 侯明善， 姚成法.基于区间系统的鲁棒H∞飞行控制系统设计[J].航空兵器， 2007（3）： 20-24.

[7] 陈龙胜， 姜长生.基于在线神经网络的无人机着陆飞行自适应逆控制器设计[J].航空兵器， 2009（3）： 22-27.

[8] Hagan M T， Demuth H B， Beale M K. Neural Network Design[M].戴葵， 译. 北京： 机械工业出版社， 2002.